Hacer comparaciones de desviación, distribución y correlación

Objetivos de aprendizaje

Después de completar esta unidad, podrá:

• Describir las comparaciones de desviación, distribución y correlación.
  
• Comprender las prácticas recomendadas para realizar comparaciones con gráficos.
  

Desviación

Las comparaciones de desviación se centran en la cantidad de diferencias que existen entre los valores y un valor base, y a veces un valor medio o valor umbral.

Gráfico de barras divergente

En el ejemplo, la longitud de las barras muestran la distancia desde un valor 0 central para indicar la cantidad de beneficios o pérdidas. Puede ver rápidamente los elementos y regiones que no son rentables.

Gráficos de líneas

Ya ha aprendido que los gráficos de líneas son una de las mejores formas de mostrar un cambios en los valores con el paso del tiempo. De manera similar, si quiere mostrar la desviación que se ha producido con el paso del tiempo, un gráfico de líneas es una buena opción. En el siguiente ejemplo, se muestra el cambio en el porcentaje del volumen de pacientes en urgencias entre el año 2015 y 2016 por mes. Como puede ver, en junio se produjo el mayor aumento en el volumen de pacientes en comparación con el año anterior.

Distribuciones

Una distribución muestra todos los valores de datos posibles y la frecuencia (recuento) de su aparición. En otras palabras, una distribución describe las veces que cada valor de datos se repite en un conjunto de datos.

Histogramas

¿Alguna vez ha utilizado una aplicación de mapas en su teléfono para conocer las horas en la que su restaurante favorito está más concurrido? Puede que haya observado el gráfico que le muestra el periodo de tiempo en el que está más concurrido. Ese gráfico es un histograma. Los picos muestran las horas más concurridas.

Un histograma es similar a un gráfico de barras, pero agrupa valores cuantitativos en intervalos de igual tamaño y cuenta la cantidad de valores en cada intervalo para que se muestren en el histograma. Al utilizar programas como Tableau, el programa determina automáticamente el tamaño del intervalo y proporciona la frecuencia (o recuento) de los valores en cada intervalo.

En el siguiente ejemplo, el histograma proporciona una vista detallada de los valores de precio de las venta de viviendas para el conjunto de datos completo. Puede ver que la mayoría de las viviendas se venden entre 100 000 $ y 200 000 $. El histograma también muestra que hay algunas viviendas con un precio más elevado comparadas con la mayoría de las viviendas.

A veces, las distribuciones pueden presentarse como porcentajes en lugar de recuentos o frecuencias.

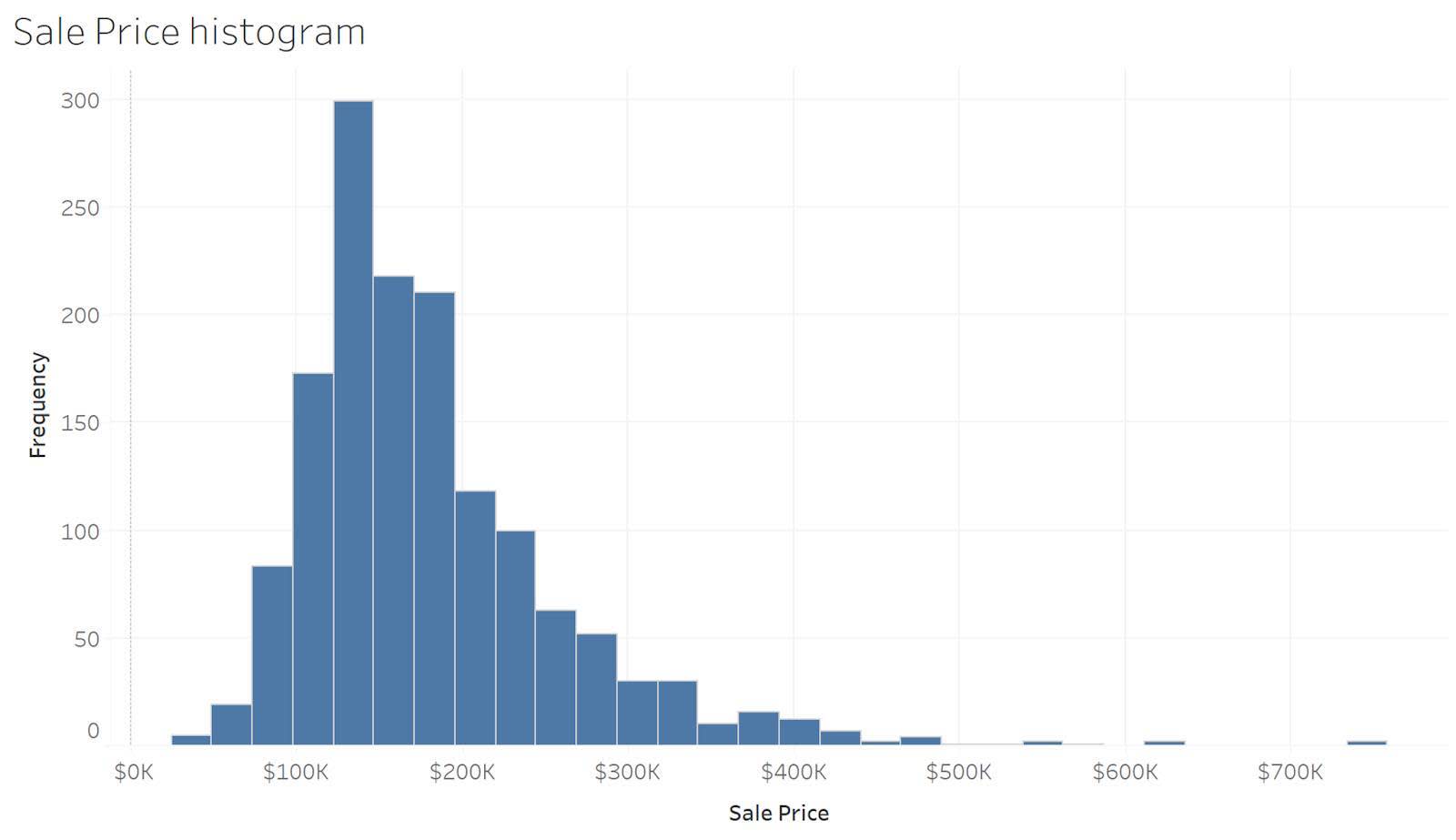
Polígonos de frecuencia

Los polígonos de frecuencia son parecidos a los histogramas, con la excepción de que utilizan líneas para conectar los recuentos de frecuencias. El siguiente ejemplo muestra los mismos datos que el histograma anterior, pero los recuentos de los intervalos están conectados por una línea. La línea proporciona una vista más limpia y sencilla para las personas.

Utilice polígonos de frecuencia en lugar de histogramas en el caso de que desee mostrar más de una distribución en el mismo gráfico.

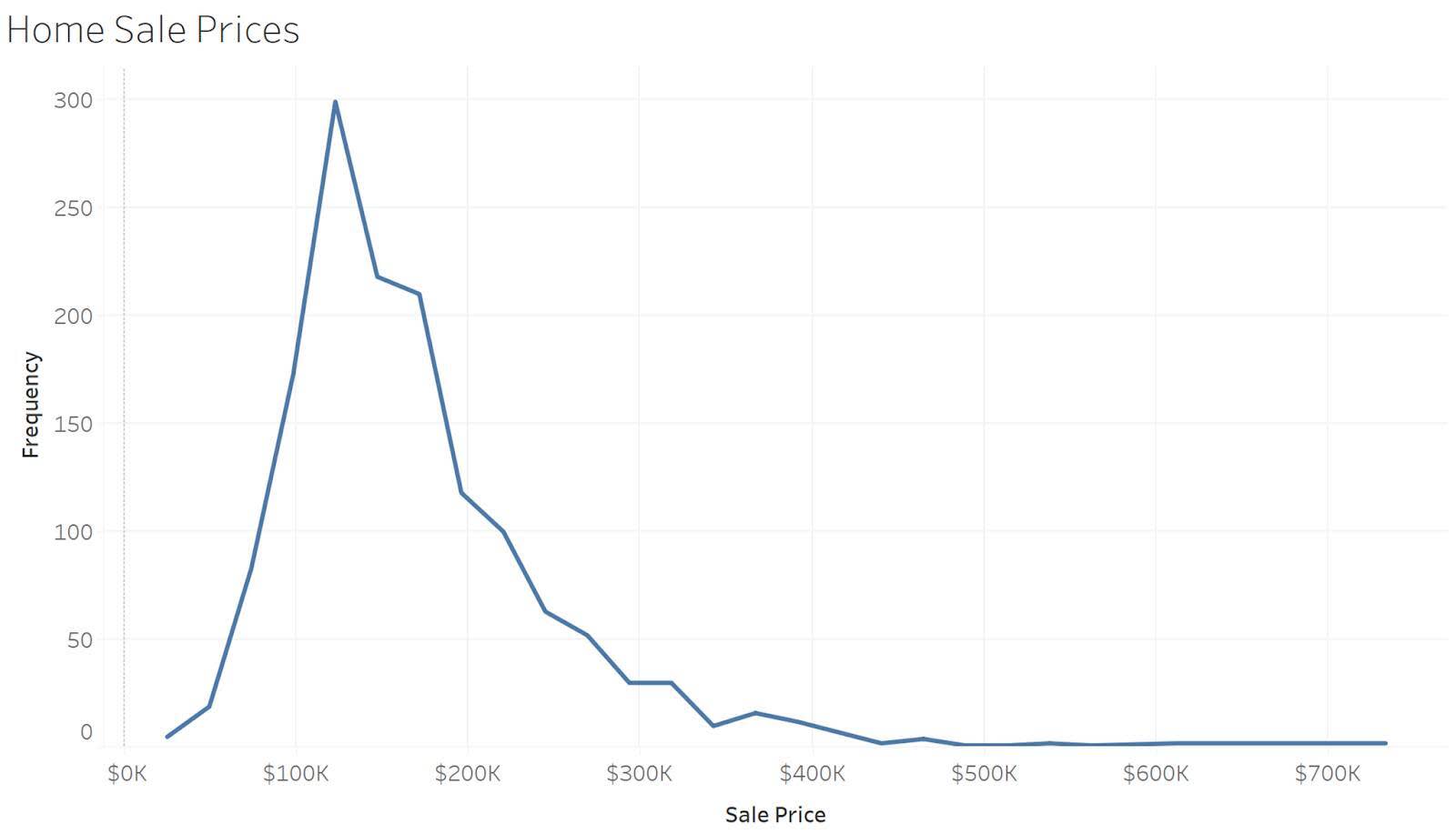
Gráficos de tiras de puntos

Los gráficos de tiras de puntos muestran puntos para cada valor de datos en una línea y ocupan mucho menos espacio que los histogramas o polígonos de frecuencia. Pueden ser una manera eficaz de mostrar el intervalo de una distribución y grupos de valores si los hubiera. Si varios valores son iguales o muy aproximados se muestran uno encima del otro, lo que dificulta poder distinguir los valores que se repiten con frecuencia en los datos.

En el siguiente ejemplo, que utiliza los mismos datos que el histograma, puede apreciar que, a pesar de que el gráfico de tiras de puntos le permite ver fácilmente cuál es la vivienda con el precio más alto, resulta difícil visualizar los precios de venta más frecuentes. Por tanto, resulta más conveniente utilizar gráficos de tiras de puntos cuando tenga conjuntos de datos más pequeños.

Hacer los puntos en un gráfico de tiras de puntos transparente hace que muchos puntos parezcan más oscuros y permite que las personas puedan distinguir entre valores únicos y varios valores similares.

Diagrama de caja y bigotes

Los diagramas de caja muestran distribuciones de una forma más compacta que los histogramas. A la hora de comparar varias distribuciones, los diagramas de caja proporcionan una manera eficaz de comparar distribuciones entre categorías. La caja de los diagramas de cajas muestra la mediana con un 50 % de los datos, o los percentiles 25 y 75, e incluye una línea que muestra el valor de la mediana, o el percentil 50.

Pero, ¿qué ocurre con los datos que se quedan fuera? Aquí es donde entran en juego los bigotes. Los bigotes, que se muestran fuera de la caja, son líneas que terminan en un trazo horizontal. Proporcionan información sobre los valores que no están dentro de esa mediana con el 50 % de los datos (la caja) y facilitan un límite para distinguir los valores atípicos. Los valores atípicos pueden entenderse como observaciones poco frecuentes o como valores que tienen una desviación extrema del centro de una distribución.

En los diagramas de caja, hay varias formas de calcular el límite en el que deberían encontrarse los posibles valores atípicos. Es posible que encuentre que algunos programas señalan los valores atípicos extremos con un símbolo diferente si dichos valores están más lejos que el límite típico.

El siguiente ejemplo compara las distribuciones de los precios de venta de viviendas de diferentes tipos de edificios. Puede ver que las viviendas unifamiliares tienen un rango de valores mucho mayor que el de cualquiera de los otros tipos de edificios, incluidas las viviendas de precios más elevados que parecen ser valores atípicos.

Este ejemplo de diagrama de cajas y bigotes también incluye tiras de puntos verticales para mostrar cada valor individual. Ahora puede ver los detalles y los puntos de datos sobre la distribución en la misma ilustración. Es posible que el hecho de aprender a interpretar los diagramas de cajas y bigotes lleve tiempo; sin embargo, estos pueden transmitir mucha información sobre una distribución sin necesidad de utilizar mucho espacio.

Consulte el módulo Distribuciones de datos en Trailhead para obtener más información sobre las distribuciones.

Correlaciones

Las comparaciones de correlaciones exploran las relaciones entre variables cuantitativas. Responden a preguntas como "¿Una variable aumenta o disminuye con respecto a otra variable?"

En estadística, el término correlación puede tener significados específicos. Por ejemplo, a la hora de hablar sobre coeficientes de correlación, hace referencia a un tipo específico de relación entre variables cuantitativas, normalmente lineales. En el módulo Correlación y regresión, aprenderá a realizar análisis de correlación y regresión.

Gráficos de dispersión

Los gráficos de dispersión se utilizan para mostrar la relación entre dos variables cuantitativas; una de ellas se muestra en el eje X y la otra en el eje Y. Los gráficos de dispersión pueden mostrar si existe una relación entre las variables. Por ejemplo, si una variable va en la misma dirección que la otra o el tipo de relación que existe, si es lineal o tiene otro patrón diferente.

La visualización de los gráficos de dispersión también puede ayudarle a ver los valores atípicos. El siguiente ejemplo muestra la relación entre el precio de venta de una vivienda y la superficie cuadrada habitable. Cada punto del gráfico de dispersión representa una vivienda unifamiliar que se ha colocado en el gráfico; en el eje Y aparece el precio de la vivienda y en el eje X la superficie cuadrada.

A pesar de que el gráfico de dispersión muestra una relación entre dos variables, no demuestra que una variable tenga algún efecto en la otra. Es posible que haya escuchado el dicho "la correlación no implica causalidad". Puede haber muchos motivos por los que se produzca una relación entre dos variables.

Líneas de tendencia

Las líneas de tendencia en los gráficos de dispersión le ayudan a visualizar el patrón general de la relación y a resumir la forma general de los datos. En el ejemplo del precio de venta de las viviendas por metro cuadrado, una línea de tendencia lineal le ayuda a ver el patrón general de la relación.

No todas las relaciones son lineales. Cuando la forma de la relación sea curva, puede utilizarse otras líneas de tendencia, como la exponencial o logarítmica.

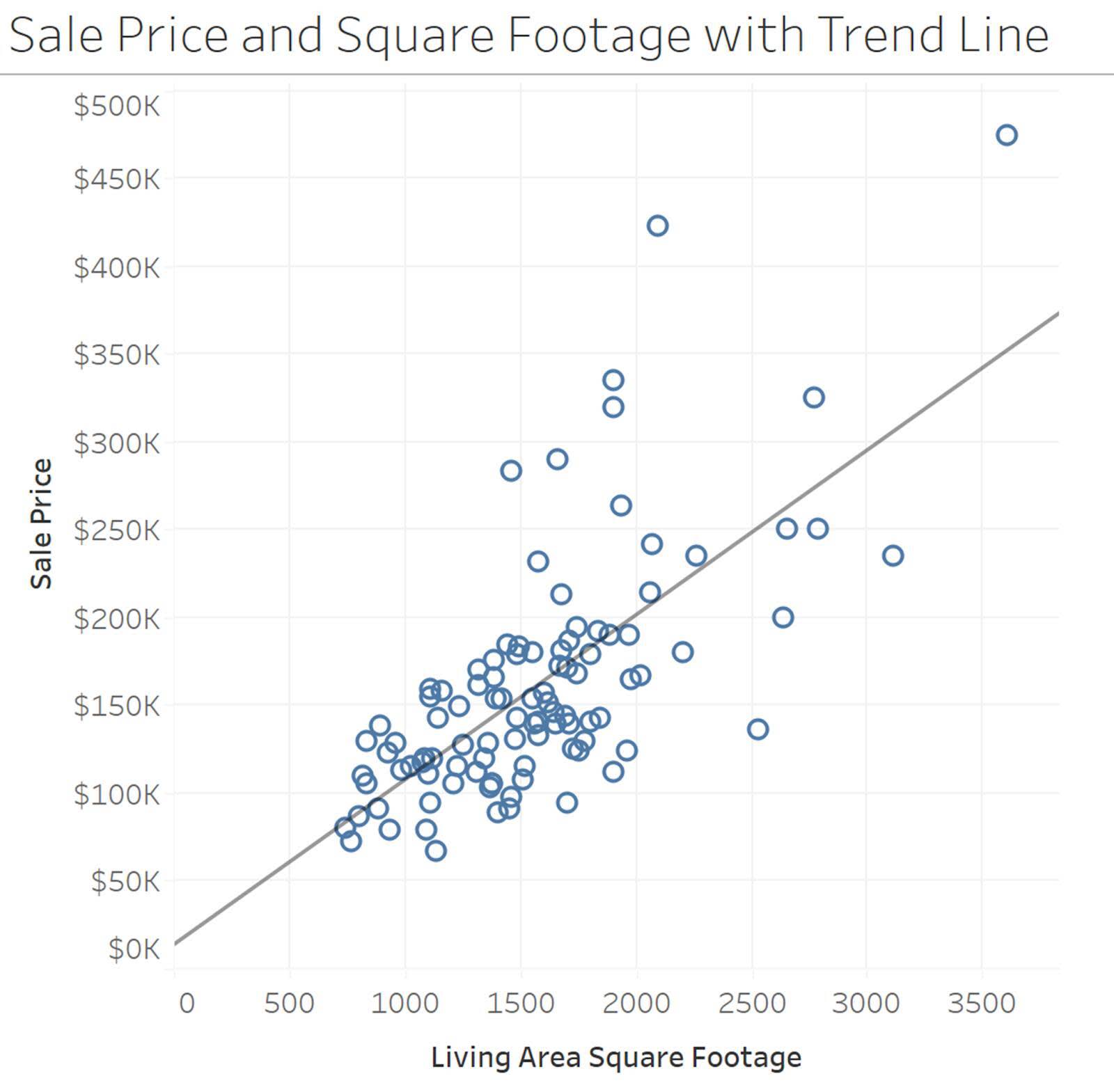
Consulte el módulo Correlación y regresión en Trailhead para obtener más información sobre la correlación y la creación de una línea de regresión lineal.

Gráficos de dispersión y burbujas, y tabla de frecuencias

Los gráficos de dispersión anteriores mostraban la relación entre dos variables cuantitativas, mostrando una de ellas en el eje X y la otra en el eje Y. Pero, ¿qué pasa si tenemos que comparar más de dos variables cuantitativas? Puede utilizar otro atributo, el tamaño, para añadir una tercera variable a un gráfico de dispersión.

En el siguiente ejemplo, el PIB per cápita y la cobertura de vacunación se muestran en el eje X e Y respectivamente, y el tamaño de cada burbuja representa el tamaño de la población.

Ya ha aprendido en este módulo que las diferencias cuantitativas de tamaño no se perciben de forma tan precisa como otros atributos, como la longitud. Al añadir una tercera variable cuantitativa a un diagrama de dispersión, no tiene muchas otras opciones; por ello, el uso de burbujas de distintos tamaños en gráficos de dispersión en un método aceptado. Al utilizar burbujas de diferentes tamaños, tenga en cuenta la pérdida de precisión al visualizar la tercera variable.

En situaciones en las que no hay muchos puntos de datos o en las que solo quiere comparar el conjunto de valores superior con el inferior de una de las variables, puede ayudarse de gráficos de barras de tipo tabla de frecuencias. Las tablas de frecuencias permiten comparar tres o más variables cuantitativas en una variable cualitativa común (categórica).

El ejemplo muestra las mismas variables que mostraba el gráfico de dispersión y burbujas, pero solo muestra los 10 países con menor cobertura de vacunación. Las tablas de frecuencias también le permiten comparar varias métricas o varios aspectos de una sola métrica.

Recursos

• Sitio web de Financial Times: Charts that work: FT visual vocabulary guide
• Trailhead: Distribuciones de datos
• Trailhead: Correlación y regresión
• Libro: Introduction to Statistics. Online Statistics Education: An Interactive Multimedia Course of Study, 2020, by David M. Lane.
• Publicación del blog Sellers Dorsey: A Histogram and Frequency Polygon Walk Into a Bar