Explorar la agregación
Objetivos de aprendizaje
Después de completar esta unidad, podrá:
- Definir qué es la agregación.
- Aplicar diferentes tipos e agregación.
¿Qué es la agregación?
La agregación se refiere a una recopilación de datos cuantitativos y puede mostrar tendencias de grandes volúmenes de datos. Por ejemplo, sumar todas las búsquedas web para un campamento específico o calcular la media de ingresos de todos los asalariados en una ciudad.
En muchas herramientas de análisis, las variables cuantitativas se agregan de forma predeterminada, pero pueden desagregarse (desglosadas por categorías) para reflejar los puntos de datos de cada valor en cada fila de la fuente de datos.
Estos son algunos ejemplos comunes de agregaciones.
Agregado |
Descripción |
Ejemplo: 3, 3, 6 |
|---|---|---|
Suma |
El total aritmético de los valores |
3 + 3 + 6 = 12 Suma = 12 |
Media |
La media aritmética de los valores (es decir, la suma dividida por el número de valores) |
3 + 3 + 6 = 12 12/3 = 4 Media = 4 |
Mediana |
El valor medio de una lista de valores ordenados de menor a mayor (o de mayor a menor) |
3, 3, 6 Mediana = 3 |
Mínimo |
El valor más pequeño |
3, 3, 6 Mínimo = 3 |
Máximo |
El valor más grande |
3, 3, 6
Máximo = 6 |
Recuento |
El número de valores (en una tabla de datos, el número de filas o registros) |
Hay tres valores
Recuento = 3 |
|
Recuento distinto (o recuento único) |
El número de valores distintos, donde cada valor único se cuenta solamente una vez (en una tabla de datos, el número de filas únicas de registros) |
Hay dos valores únicos, 3 y 6
Recuento distinto (o recuento único) = 2 |
Ejemplos de agregaciones
Vamos a ver algunos ejemplos de agregaciones y el impacto que tienen en el análisis de datos. Vamos a utilizar datos de encuesta asociados a una prueba de vocabulario en línea. Cada participante realizó un cuestionario de vocabulario en línea y, después, respondió algunas preguntas demográficas sobre sí mismo.
Ver una visualización con una variable cuantitativa agregada
Vamos a consultar la variable cuantitativa Age (Edad) en la siguiente visualización. Observe que la agregación de Sum (Suma) suma todos los valores de la variable Age (Edad) y da un total de 420 085 años.

En el gráfico anterior, una sola barra resume todos los datos (12 168 filas) del conjunto de datos como un único número.
Este valor de Sum ofAge (Suma de edad) se puede desglosar por el nivel de formación más alto, lo que da como resultado una barra que muestra la edad total para cada nivel educativo. (Si suma cada uno de estos valores, es lo mismo que el total de la barra única. 116 602 + 160 542 + 120 351 + 22 092 + 498 = 420 085).

Importante: La suma no es una agregación apropiada para este ejemplo, ya que una edad de 116 602 años no es significativa. Para algunas variables, como la edad en este ejemplo, el uso de la suma como agregación no es una representación útil o adecuada de los datos. (En otros ejemplos, la suma puede ser una agregación apropiada). Al crear o ver visualizaciones, es importante prestar atención a las agregaciones que se utilizan en análisis y gráficos.
Ver los datos subyacentes
Para comprender mejor qué valores se totalizan, vamos a ver los datos sin procesar. Cuando examina los datos a nivel de fila, puede observar una fila para cada participante y su nivel educativo y edad.

Si se observa el nivel educativo Choose not to say (Prefiero no decirlo), la suma de Age (Edad) es 498.
13 + 13 + 13 + 13 + 15 + 16 + 16 + 16 + 17 + 17 + 18 + 20 + 20 + 23 + 37 + 45 + 53 + 65 + 68 = 498 años
Ver el impacto de la agregación media
Vamos a volver a mirar el mismo gráfico de barras que antes, pero vamos a cambiar la agregación a "media". En lugar de sumar todas las edades y mostrar ese valor, ahora la altura de las barras es su media aritmética. Para cada nivel educativo, se suman todas las edades y se dividen por el número de valores.

Si analizamos el nivel educativo Choose not to say (Prefiero no decirlo) (se muestra en celeste), la media es 26,21 años.
13 + 13 + 13 + 13 + 15 + 16 + 16 + 16 + 17 + 17 + 18 + 20 + 20 + 23 + 37 + 45 + 53 + 65 + 68 = 498
498 ÷ 19 = 26,21
Ahora los números son edades que parecen realistas para una persona (aproximadamente, de 20 a 43 años). Además, como indica la media, los encuestados más jóvenes tienen menos formación.
Ver el impacto de la agregación mediana
Vamos a ver qué ocurre cuando se agrega Age (Edad) como mediana en un conjunto de datos. Los valores extremos pueden ampliar o sesgar los promedios. Por ejemplo, si una persona de 103 años realizó el cuestionario, su edad podría hacer que pareciera que su categoría educativa tenía participantes de mayor edad en general. Para evitar el problema de sesgo debido a los valores extremos, la agregación de MEDIANA clasifica todos los valores en orden (de mayor a menor o de menor a mayor) y devuelve el valor medio.

Si analizamos el nivel educativo Choose not to say (Prefiero no decirlo) (se muestra en celeste), la mediana de la edad es 17 años.
13, 13, 13, 13, 15, 16, 16, 16, 17, 17, 18, 20, 20, 23, 37, 45, 53, 65, 68
En este gráfico, podemos ver que la mediana de la edad es un poco más baja. En otros casos, se podría esperar una mediana más baja si no hay límite de edad para realizar el cuestionario, pero aquí los participantes deben tener al menos 13 años para participar. Esto significa que no puede haber valores extremos jóvenes que hagan bajar la media. Además, las tendencias generales siguen apareciendo: cuanto más nivel educativo, mayores son los participantes.
Explorar el impacto de las agregaciones mínimo y máximo
La agregación mínima devuelve el valor más bajo en los datos seleccionados, mientras que la agregación máxima devuelve el valor más alto.

Si analizamos el nivel educativo Choose not to say (Prefiero no decirlo) (se muestra en celeste), la edad mínima es 17.
13, 13, 13, 13, 15, 16, 16, 16, 17, 17, 18, 20, 20, 23, 37, 45, 53, 65, 68

Si analizamos el nivel educativo Choose not to say (Prefiero no decirlo) (se muestra en celeste), la edad máxima es 68.
13, 13, 13, 13, 15, 16, 16, 16, 17, 17, 18, 20, 20, 23, 37, 45, 53, 65, 68
Ver el impacto de la agregación recuento
Ahora, vamos a ver qué sucede si la edad se agrega como recuento. Un recuento devuelve el número de valores de los datos de la categoría seleccionada. Esto significa que ya no nos fijamos en la edad, sino en el número de participantes.
Si se observa el nivel educativo Choose not to say (Prefiero no decirlo), el recuento es 19 y el recuento distinto es 12. El conteo distinto es 12 porque cuatro participantes tenían 13 años, dos participantes tenían 16 y dos tenían 20 años. Contamos 12, 13 y 20 solo una vez porque la agregación recuento distinto cuenta solo los valores únicos.
|
El recuento es 19 13 13 13 13 15 16 16 16 17 17 18 20 20 23 37 45 53 65 68 |
Mientras que el recuento distinto es 12 13 15 16 17 18 20 23 37 45 53 65 68 |
|---|
Los recuentos nos muestran que son muy pocos los participantes que se negaron a proporcionar su nivel educativo.
Ejemplo de desagregación
El primer gráfico que observó era una vista completamente agregada de los datos: había solo un valor, la suma general. Luego, el conjunto completo de datos se desagregó por nivel educativo para mostrar el desglose de la suma de edades para cada nivel educativo. En lugar de observar la suma (o la media o el mínimo) de todas las edades en el conjunto de datos, cada barra se agrega al nivel de cada categoría educativa. Los datos todavía están agregados, pero a un nivel más detallado.
|
|
|---|
Ahora, vamos a tener en cuenta los datos originales de nuevo.
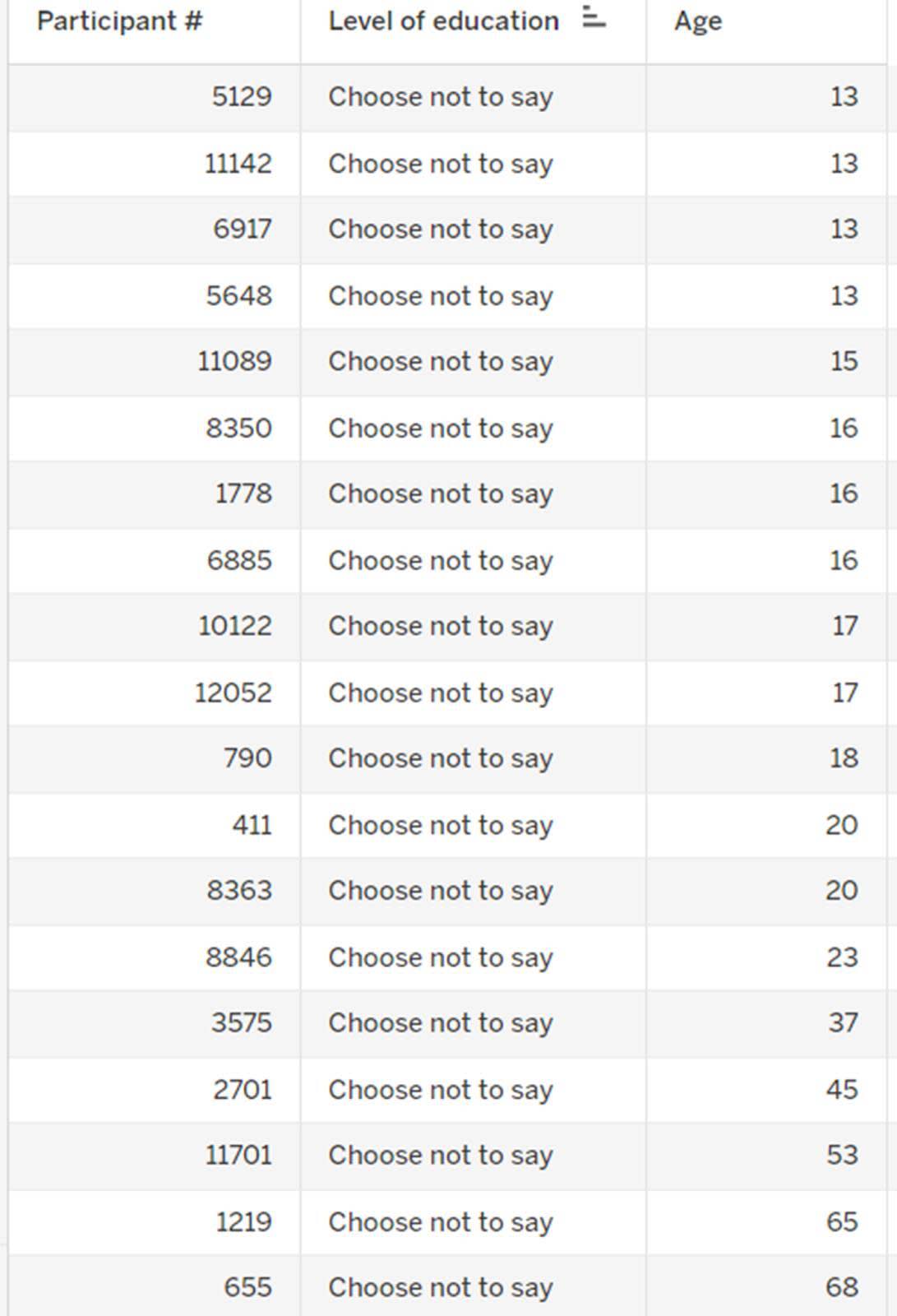
Cada fila representa un participante. Si quisiéramos ver la edad de cada participante en lugar de un valor agregado, podríamos desagregar completamente los datos o trazar cada punto en el conjunto de datos.
Ver el impacto de los datos desagregados

Este gráfico utiliza fluctuación para distribuir los puntos o marcas de datos. La fluctuación se refiere a colocar aleatoriamente las marcas a lo largo de un eje que no tiene intervalos (aquí, el eje X) para ayudar a revelar la densidad de los datos. Si no hubiera fluctuación, todas las marcas se apilarían en una única línea vertical por nivel educativo. En un gráfico de nube, la ubicación horizontal de una marca es aleatoria y no transmite ningún significado particular.
En esta visualización, podemos ver que hay más participantes jóvenes y menos participantes a medida que aumenta la edad. También podemos ver que, aunque hay algunos participantes mayores en la categoría Less than high school (Inferior a secundaria), la mayoría de ellos son bastante jóvenes (menores de veinte años). La categoría High school (Secundaria) tiene la mayor cantidad de edades alrededor de los 20 años, lo que podría indicar que actualmente son estudiantes universitarios. También hay muy pocos participantes con títulos de posgrado menores de 20 años. Los datos desagregados coinciden bastante bien con las expectativas realistas basadas en lo que sabemos sobre la edad y el nivel educativo.
Póngase a prueba
Reto: Tiene la siguiente tabla con tres filas de datos sobre los lectores de periódicos por semana.
Nombre |
Periódicos leídos por semana |
|---|---|
Brooklyn |
2 |
Morgan |
3 |
Vaida |
7 |
¿Cómo se agregarían los valores de la variable Periódicos leídos por semana (2, 3 y 7) como suma, media, mediana, mínimo, máximo y recuento? Tómese un momento para pensar en ello y, después, compruebe sus respuestas usando las tarjetas interactivas que se muestran a continuación.
Lea el tipo de agregación en cada tarja, piense cuál sería el valor para esa agregación y, después, haga clic en la tarjeta para ver la respuesta correcta. Haga clic en la flecha hacia la derecha para ir a la siguiente tarjeta y en la flecha hacia la izquierda para volver a la tarjeta anterior.
Ha explorado la manera en la que las agregaciones inciden en los datos y el efecto que se produce al desagregar los datos. En la siguiente unidad, vamos a profundizar en estos conceptos y aprenderá sobre granularidad.
Recursos


