用柱状图展示连续变量的分布

学习目标

完成本单元后，您将能够：

• 认识连续变量的分布形态。
• 描述如何用柱状图呈现数据的分布。

在上一个单元，您看到了离散变量的分布（糖果的颜色）。您认识到离散变量的值是分开的，泾渭分明，而连续变量的值形成不间断的整体。本单元中，您将探索连续变量的分布以及如何用柱状图来表示。

以下示例改编自在线统计学教育：多媒体学习课程中关于分布的篇章。项目领导：David M. Lane，莱斯大学。

在一系列 20 次试验中，其中一位作者记录了他把光标移到某个目标上的响应时间。“响应时间”这个变量是连续的，以毫秒为单位计量时间时，没有两次响应时间是一样的。

下图显示这些响应时间，单位是毫秒。

响应时间的分组频率分布

回顾您在上一个单元中学过的频率分布。如果您用频率分布来表示上表中的响应时间值，那么会有 20 个不同的值，每个值频率为 1。没有多大意义。 

为了解决这个问题，您可以创建分组频率分布，把在各个同等大小柱子（数值区间）内的响应时间制成表，如下表所示。

您可以通过柱状图图形化展示分组频率分布。x 轴上的标签是它们所代表的柱子的中间值。 

我们稍后会详细介绍柱状图。首先，我们来看不同的分布形态以及它们所透露的柱状图数据。

分布形态

分布呈现不同形态。分布可以是对称的，意思是所有值围绕中心均匀地分布。或者，分布可以呈现正偏态，更多的值集中在右边，或者是负偏态，更多的值集中在左边。

试想您测量了三个不同组的人员的身高，并且您绘制了每个组的柱状图，来展示该组人员的身高分布。

柱子的大小是 2.95 英寸，因此人员的身高用柱子表示分别为 59–61.95 英寸、62–64.95 英寸，以此类推。（Tableau Desktop 自动为我们生成柱子大小。）

我们来研究每个分布形态。在下文所示的每个分布图中，请注意平均值和中位数（数据点的中间值）决定了形态。 

对称分布

在我们的例子中，其中一个组的身高分布几乎是对称的。如果您把它对折，两边几乎完美吻合。

在一个完全对称的分布中，数据的中心既是平均值也是中位数（数据点的中间值），因为这两个值相等。数据的中心用这两个值都可以表示，数据的分布在中心的两侧延伸出去同等距离。

正偏态分布

有些分布是不对称的。如果某个分布中的数据在正方向上延伸出去比负方向上远，那么它属于正偏态分布。正偏态也叫右偏态，因为数据向右延伸。右“尾”更长。当分布呈现正偏态时，中位数小于平均值。

比如，试想一座居民中有几位亿万富翁的城市。那些亿万富翁的高收入将使该城市的平均收入出现偏离。平均收入将看起来高于准确值。为了真实反映所有城市居民的经济状况，中位数收入将是更好的选择。

同理，看我们的身高数据时，有一个组呈现正偏态，原因是有三个人的身高接近或超过 72 英寸（6 英尺）。他们如此高的身高拉高了平均值。通过中位数来呈现这个组的身高也是一个更好的选择。

负偏态分布

另一种不对称分布是负偏态分布。负偏态分布中的数据在负方向上比在正方向上延伸出去更远。负偏态也叫左偏态，因为数据向左延伸。左“尾”更长。当分布呈现负偏态时，中位数大于平均值。

比如，试想一个拥有 20 名学生的班级。在这个班级中，有两名学生从来不上课，也不做作业。这两名学生的期末成绩是 0.0 分。他们 0.0 分的成绩将使全班的平均分出现偏离，从而使学生的平均成绩看起来低于准确值。为了真实反映这个班级的学生成绩，分数的中位数将是更好的选择。

同理，看我们的身高数据时，有一个组呈现负偏态，原因是有几个人的身高低于 60 英寸（5 英尺）。他们很低的身高拉低了平均值。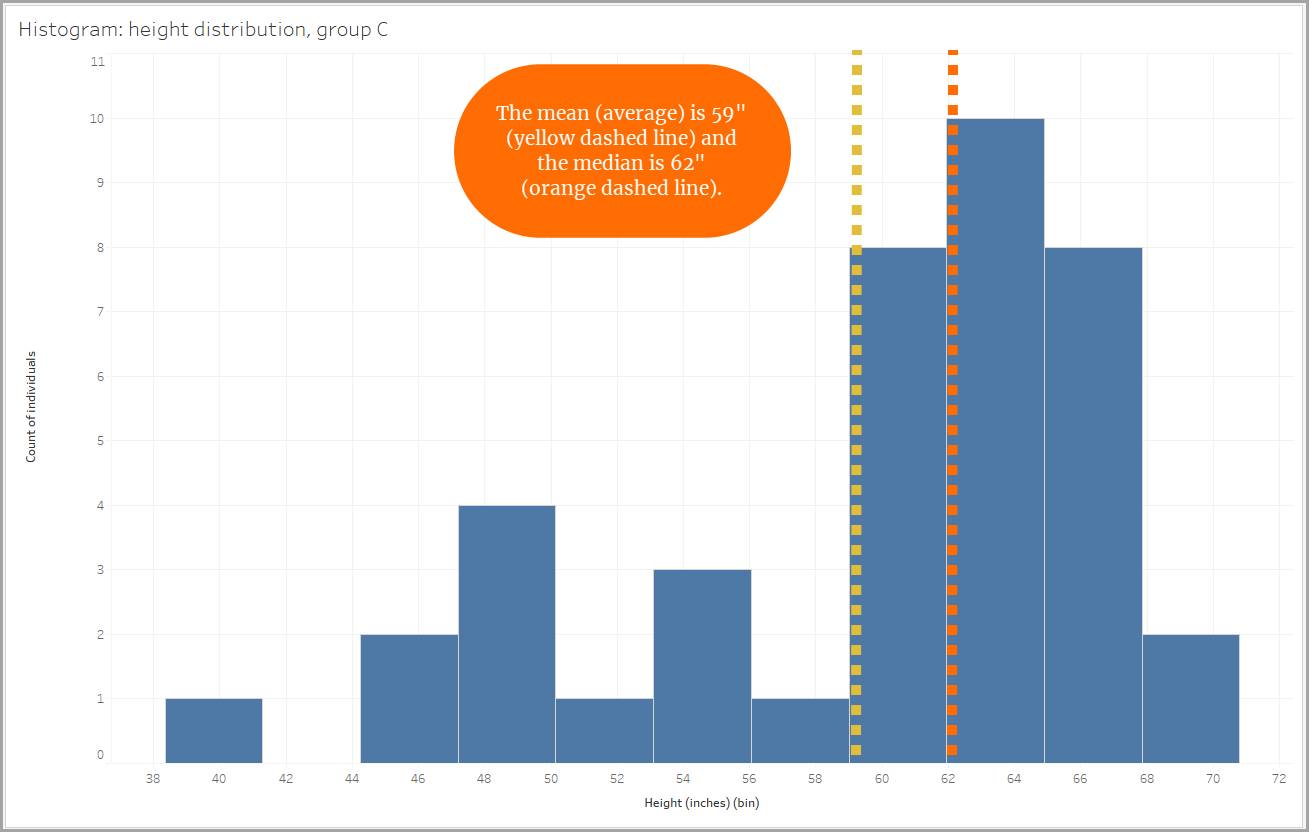

柱状图

您在本单元中看过的所有图形都是柱状图。柱状图看起来与条形图类似，但是它把连续变量的值分组成同等大小的区间，即柱子。 

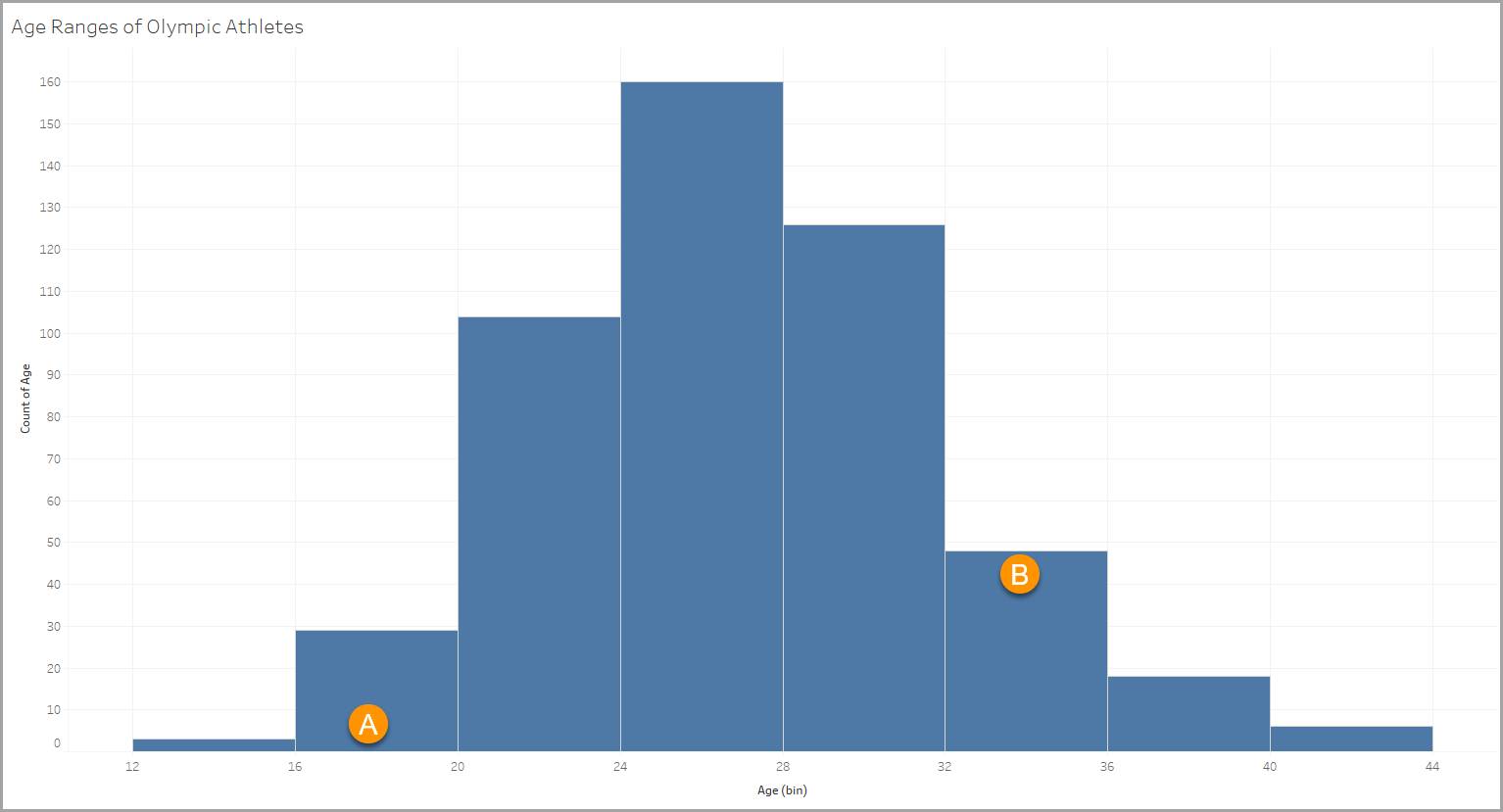
这张柱状图采用一个关于奥运会运动员信息的数据集。该数据集中的其中一个变量包含运动员的年龄，在 18 到 90 岁之间。从这张柱状图中，您可以看出运动员如何细分为不同的年龄组。

柱子

每根柱子代表一个四岁的年龄区间，比如 12–15、16–19 (A)、20–23、24–27，等等。 

柱子

每根柱子代表符合柱子（这里是年龄区间）条件的项目数量。在我们的例子中，有 48 名运动员属于 32–35 这个年龄区间 (B)。

您看了以柱状图表示的连续变量分布。在下一个单元，您将学习用箱形图查看连续变量的分布。

资源

• 网站：David M. Lane 的公开著作，《统计学入门》
• Tableau 帮助：绘制柱状图