用箱形图展示连续变量的分布
学习目标
完成本单元后，您将能够：
- 描述如何用箱形图代表数据的分布。
- 绘制箱形图。
目前为止您已经了解了若干展示变量分布的方式。本单元中，您将学习另一种重要图形，称作箱形图。箱形图是美国数学家 John Tukey 在 20 世纪 70 年代发明的，以图形化的方式一目了然地展示和比较数据的分布。
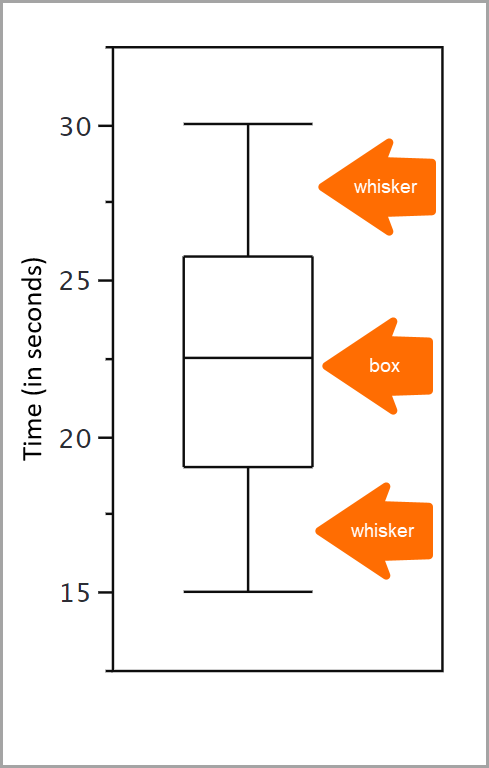
箱形图中的箱体展示数据的中间 50%。数据从第 25 个百分位延伸到第 75 个百分位，中位数在第 50 个百分位。
百分位表示某个分数与同一个数据集中的其他分数相比如何。例如，您可以做一个测验来衡量自己的内向程度。光有您一个人的内向评分，是很难解释的。您想看看您的评分与别人相比如何，并且想知道害羞程度评分低于您的人数占比。这个百分比是一个百分位。如果 65% 的其他测试对象的评分显示没有您那么害羞，那么您的评分处于第 65 个百分位。
为了检查结果，箱形图中的箱体展示数据的中间 50%，即从第 25 个至第 75 个百分位。但是在这个区间之外的数据呢？那是箱须出现的地方。箱须画在箱体之外，是在水平横线处截断的垂直线条。箱须让您可以洞察不在数据的中间 50%（箱体）范围内的数值，包括异常值。异常值可以理解为非典型、不经常出现的观察，或是极端偏离分布中心的值。
我们将在本单元后面更详细地来看所有这些概念。
绘制箱形图
下面的箱形图例子改编自 David M. Lane 的著作在线统计学教育：多媒体学习课程中关于箱形图的篇章。项目领导：David M. Lane，莱斯大学。
作者采用了对 31 名学生的一次课堂实验。给学生们每人发了一张纸，上面有 30 个彩色矩形，他们的任务是尽快说出颜色。
以秒为单位记录了他们花的时间，如下表所示。
|
14 |
17 |
18 |
19 |
20 |
21 |
|
15 |
17 |
18 |
19 |
20 |
22 |
|
16 |
17 |
18 |
19 |
20 |
23 |
|
16 |
17 |
18 |
20 |
20 |
24 |
|
17 |
18 |
18 |
20 |
21 |
24 |
| 29 |
我们用这个数据集来绘制箱形图。这是绘制箱形图所需的步骤简介。
- 计算百分位。
- 根据百分位绘制箱形图。
- 确定步进大小。
- 添加箱须。
- 添加异常值。
计算百分位
记住箱形图中的箱体从数据的第 25 个百分位延伸到第 75 个百分位。第 50 个百分位画在箱体里面。箱体的底部（即下边缘）是第 25 个百分位，箱体的顶部（即上边缘）是第 75 个百分位。
在下面的步骤中，我们用一根数线来看百分位。
-
从小到大排列分数。
-
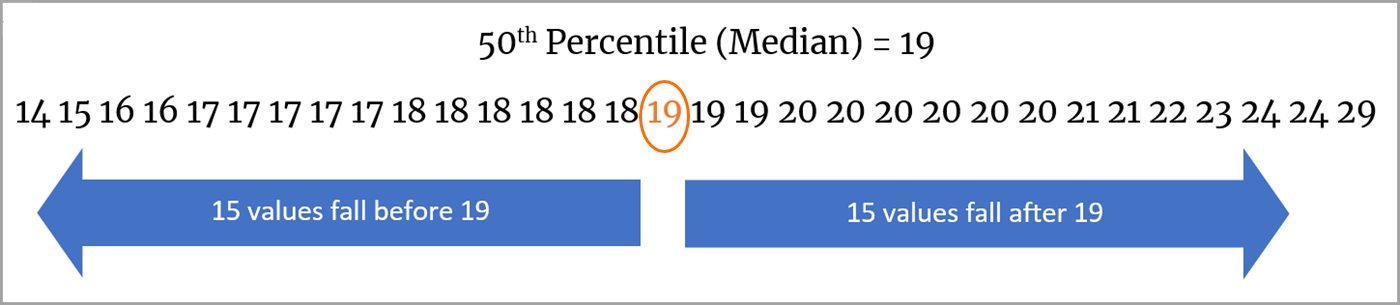
确定中位数，即中间值。中位数出现在一个数字序列的开头和结尾的正中间。对于包含 31 个值的序列，中间表示中位数前面有 15 个值，后面也有 15 个值。因此，中位数是 19。
-
确定第 25 个百分位。第 25 个百分位的值出现在序列的开头和中位数之间的正中间。在我们的例子中，有 31 个值，中间位置前面有 7 个值，在它和中位数之间有 7 个值。因此，第 25 个百分位的值是 17。
-
确定第 75 个百分位。第 75 个百分位的值出现在中位数和序列结尾之间的正中间。我们的列表有 31 个值，这里的中间位置和中位数之间有 7 个值，在它和序列结尾之间也有 7 个值。因此，第 75 个百分位的值是 20。
根据百分位绘制箱形图
我们来插入那些值，画出箱体。
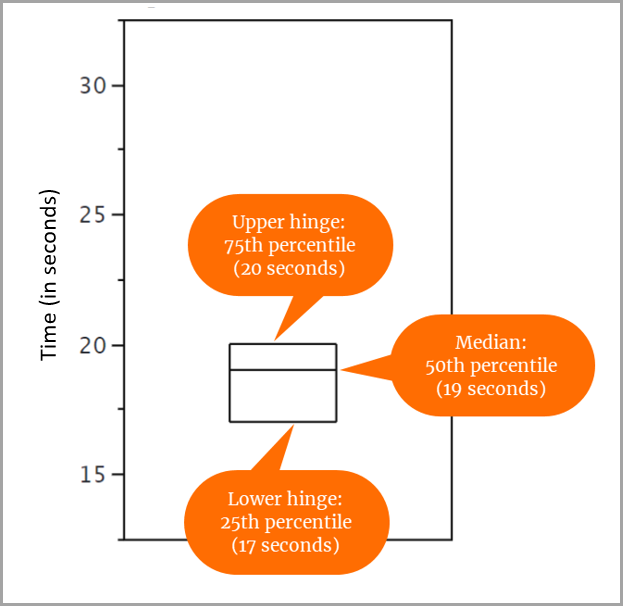
对于包含 31 个分数的数据集，我们确定了：
- 第 25 个百分位是 17。
- 第 50 个百分位（中位数）是 19。
- 第 75 个百分位是 20。
所以，您这样来画箱体。
- 第 25 个百分位（下边缘）与 y 轴上的 17 对齐。
- 第 50 个百分位（中位数）与 y 轴上的 19 对齐。
- 第 75 个百分位（上边缘）与 y 轴上的 20 对齐。
数据值的中间 50% 出现在箱体里。
备注：介于第 25 个百分位和中位数之间的值也叫第二四分位，介于第 51 个百分位（紧接在中位数后面）和第 75 个百分位之间的值也叫第三四分位。比第 25 个百分位小的值也叫第一四分位，在第 75 个百分位之上的值也叫第四四分位。用箱须及其他标记来标注第一和第四四分位的值。
确定步进大小
现在您准备绘制箱体上面和下面的箱须，提供关于数据分布的补充信息。箱须的放置由步进决定，一个步进相当于 1.5 x IQR。IQR 代表四分位距。
这听起来有点复杂，不过简单地说，IQR 是指上边缘（第 75 个百分位）的值和下边缘（第 25 个百分位）的值之间的差。记住，数据值的中间 50% 出现在箱体里，箱体以这些值为界限。
在我们的分数集合中，上边缘的值是 20，下边缘的值是 17。因此，IQR 等于 20 减 17，即 3。
为了确定步进大小，将 3 (IQR) 乘以 1.5，得到 4.5，这就是步进大小。
添加箱须
为了理解如何绘制箱须，我们先来看几个名词，以及如何将其应用到我们的例子中的分数上。
箱须放在哪里？
您可以从上边缘到上方的相邻值，从下边缘到下方的相邻值画出箱须。
箱须不会一直延伸到异常值。相反，您用一个小 o 代表异常值，用星形 (*) 代表极端的异常值。
对于我们的分数数据，箱须从上边缘值 (20) 延伸到上方的相邻值 (24)，从下边缘值 (17) 延伸到下方的相邻值 (14)。
添加异常值
超出内限但是没有超出外限的值属于异常值。这些值中有一个在我们的分数集合内，29，与外限的值吻合，但是没有超出它。用小 o 来描绘这个值。
这样，您的箱形图就完整了！
箱形图与柱状图比较
您可能在想箱形图与柱状图相比在展示分布上有何不同。
- 柱状图用柱子来绘制数值的频率。
- 在箱形图中，数据的中间 50% 出现在箱体里，异常值（如有）画在箱须外面。
为了对这种图形有个概念，我们回到展示人的身高分布形态的数据。比较数据在柱状图和箱形图中的呈现。
请注意箱形图有多么节省空间；这样比较分布情况更容易。通过箱形图，比较三幅并排的分布图比柱状图更容易。我们再看几个例子。
您现在已经了解了分布如何帮助您探索、了解和传播数据。
