Fazer comparações de desvios, distribuições e correlações
Objetivos de aprendizagem
Após concluir esta unidade, você estará apto a:
- Descrever comparações de desvio, distribuição e correlação.
- Entender as melhores práticas para fazer comparações com gráficos.
Desvio
As comparações de desvio estão centradas na quantidade de valores que diferem de um valor de linha de base, por vezes um valor médio ou limite.
Gráficos de barras divergentes
No exemplo, o comprimento das barras indica a distância de um valor central de zero para mostrar a quantidade de lucro ou perda. Assim, é possível ver rapidamente quais itens e regiões não são lucrativos.
Gráficos de linhas
Anteriormente, você viu como os gráficos de linhas são uma das melhores maneiras de mostrar uma mudança nos valores ao longo do tempo. Da mesma forma, quando você quiser mostrar o desvio ao longo do tempo, um gráfico de linhas é uma boa opção. No exemplo a seguir, é mostrada a variação percentual do volume de pacientes atendidos nas emergências entre 2015 e 2016 para cada mês. Você pode ver que junho teve o maior aumento no volume de pacientes em relação ao ano anterior.
Distribuições
Uma distribuição mostra todos os valores de dados possíveis e a frequência (contagem) da ocorrência. Em outras palavras, uma distribuição descreve quantas vezes cada valor de dados ocorre em um conjunto de dados.
Histogramas
Você já usou um aplicativo de mapas no telefone para pesquisar os horários de pico do seu restaurante favorito? Talvez tenha reparado no gráfico que mostra as horas de maior movimento. Esse gráfico é um histograma. O pico indica a hora de maior atividade.
Um histograma é semelhante a um gráfico de barras, mas agrupa valores quantitativos em intervalos de tamanho igual, ou compartimentos, e conta quantos valores estão em cada compartimento para exibir o histograma. Com programas como o Tableau, o programa determina automaticamente o tamanho do compartimento e apresenta a frequência (ou contagem) dos valores em cada compartimento.
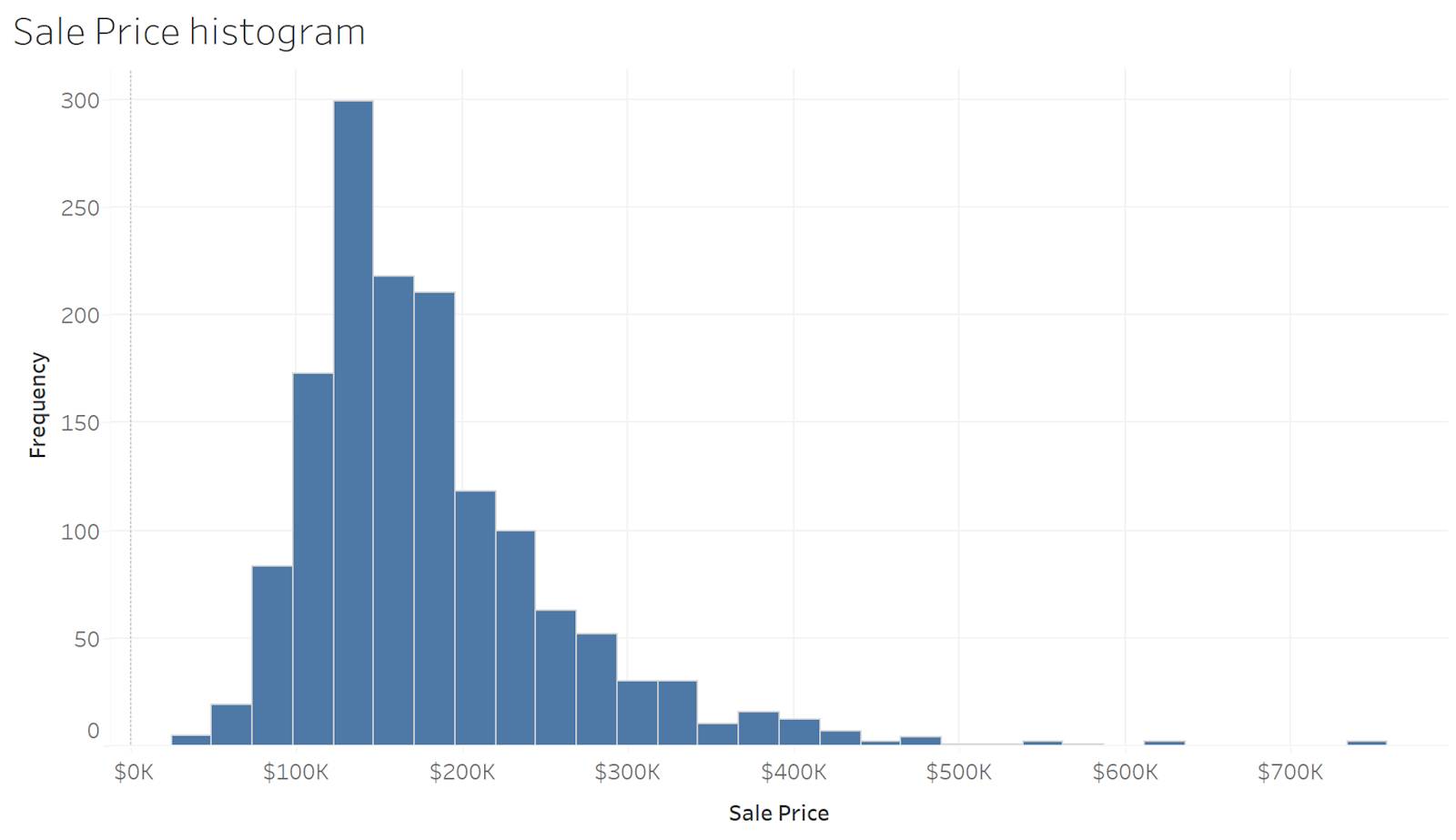
No exemplo a seguir, o histograma apresenta uma visão detalhada dos valores de preço de venda de imóveis para todo o conjunto de dados. É possível ver que a maioria dos imóveis está sendo vendida entre US$ 100 mil e US$ 200 mil. O histograma também mostra que há alguns imóveis com preços mais altos em comparação com a maioria dos imóveis.
Algumas vezes, as distribuições podem ser apresentadas como porcentagens em vez de contagens ou frequências.
Polígonos de frequência
Os polígonos de frequência são semelhantes aos histogramas, mas usam linhas para unir as contagens de frequência. O exemplo a seguir mostra os mesmos dados do histograma acima. Porém, as contagens em cada compartimento estão unidas por uma linha. A linha oferece ao visualizador um aspecto mais limpo e simples.
Use polígonos de frequência em vez de histogramas quando quiser mostrar mais que uma distribuição no mesmo gráfico.
Diagramas de dispersão
Os diagramas de dispersão mostram um ponto para cada valor de dados em uma linha e ocupam muito menos espaço do que histogramas ou polígonos de frequência. Os diagramas de dispersão podem ser uma forma eficiente de mostrar o intervalo de uma distribuição e se existe algum agrupamento de valores. Se vários valores forem iguais ou muito próximos uns dos outros, eles serão representados sobrepostos, dificultando a distinção dos valores que ocorrem frequentemente nos dados.
No exemplo a seguir, que usa os mesmos dados que o histograma, é possível ver que, embora o diagrama de dispersão permita ver facilmente imóveis com preços mais elevados, é difícil ver os preços de venda mais frequentes. Portanto, é melhor usar diagramas de dispersão quando os conjuntos de dados são menores.
Ao tornar transparentes os pontos de um diagrama de dispersão, você pode permitir que vários pontos sejam exibidos em um tom mais escuro, permitindo que o visualizador distinga entre valores únicos e vários valores semelhantes.
Diagramas de caixa
Os diagramas de caixa apresentam as distribuições de uma forma mais compacta do que um histograma. E, ao comparar várias distribuições, os diagramas de caixa oferecem uma forma eficiente de comparar distribuições entre categorias. A caixa de um diagrama de caixa mostra os 50% do meio dos dados, ou o percentil de 25-75, e inclui uma linha que mostra o valor mediano, ou percentil 50.
Mas e os dados que estão fora disso? É aí que as retas entram. Plotadas fora da caixa, as retas são linhas verticais que terminam em um curso horizontal. Elas fornecem informações sobre os valores que não estão dentro dos 50% do meio dos dados (a caixa) e estabelecem um limite para distinguir os valores discrepantes. As discrepâncias podem ser entendidas como observações atípicas e pouco frequentes, ou como valores que têm um desvio extremo do centro de uma distribuição.
Nos diagramas de caixa, há várias formas de calcular o limite onde os potenciais valores discrepantes devem estar. Em alguns programas, valores discrepantes extremos podem ser assinalados com um símbolo diferente se esses valores estiverem mais afastados do que o limite típico.
O exemplo a seguir compara as distribuições de preços de venda de imóveis para diferentes tipos de construção. Você pode ver que os imóveis para uma única família têm um intervalo de valores muito maior do que qualquer outro tipo de construção, incluindo muitos imóveis com preços mais altos que parecem ser valores discrepantes.
Esse exemplo de diagrama de caixa também inclui diagramas de dispersão vertical para mostrar cada valor individual. Agora é possível ver todos os pontos de dados e detalhes sobre a distribuição no mesmo elemento visual. Embora possa ser necessário algum tempo para aprender a interpretar os diagramas de caixa, eles podem transmitir muitas informações sobre uma distribuição sem ocupar muito espaço.
Consulte o módulo Distribuições de dados no Trailhead para saber mais sobre distribuições.
Correlações
As comparações correlativas exploram as relações entre variáveis quantitativas. Elas respondem a perguntas como: “Uma variável aumenta ou diminui com outra variável?”
Em estatística, o termo correlação pode ter significados específicos. Por exemplo, ao falar sobre coeficientes de correlação, isso se refere a um tipo específico de relação entre variáveis quantitativas, geralmente linear. No módulo Correlação e regressão, você aprende a realizar análises de correlação e regressão.
Gráficos de dispersão
Os gráficos de dispersão são usados para mostrar o relacionamento entre duas variáveis quantitativas com uma variável apresentada no eixo x e a outra no eixo y. Os gráficos de dispersão podem mostrar se existe um relacionamento entre as variáveis. Por exemplo, se uma variável “vai na mesma direção” que a outra e que tipo de relacionamento está presente, como um padrão linear ou diferente.
A visualização de gráficos de dispersão também pode ajudar a identificar valores discrepantes. O exemplo a seguir mostra o relacionamento entre o preço de venda de um imóvel e a metragem quadrada da área habitável. Cada ponto no gráfico de dispersão representa um único imóvel colocado no gráfico usando o preço de venda do imóvel no eixo y e a metragem quadrada no eixo x.
Embora um gráfico de dispersão possa mostrar um relacionamento entre duas variáveis, não prova que uma variável esteja afetando a outra. Talvez você já tenha ouvido o ditado: “A correlação não prova a causalidade”. Pode haver muitas razões para o relacionamento entre as variáveis.
Linhas de tendência
As linhas de tendência em gráficos de dispersão ajudam a ver o padrão geral do relacionamento e resumem a forma geral dos dados. No nosso exemplo de preço de venda de imóveis e metragem quadrada, uma linha de tendência linear ajuda a ver o padrão geral do relacionamento.
Nem todos os relacionamentos são lineares. Quando a forma do relacionamento é curva, linhas de tendência como exponencial ou logarítmica podem ser usadas para substituir a linear.
Consulte o módulo Correlação e regressão no Trailhead para saber mais sobre correlação e criação de uma linha de regressão linear.
Gráficos de dispersão de bolhas dimensionadas e Table Lens
Os gráficos de dispersão anteriores mostraram o relacionamento entre duas variáveis quantitativas com uma variável apresentada no eixo x e a outra no eixo y. Mas o que fazer quando você quiser comparar mais do que duas variáveis quantitativas? Há outro atributo, o tamanho, que pode ser usado para adicionar uma terceira variável a um gráfico de dispersão.
No exemplo a seguir, o PIB per capita e a cobertura da vacinação são apresentados nos eixos x e y, respetivamente, com o tamanho de cada bolha representando a dimensão da população.
Você viu anteriormente nesse módulo como os visualizadores não percebem as diferenças quantitativas de tamanho com tanta precisão quanto outros atributos, como o comprimento. Ao adicionar uma terceira variável quantitativa a um gráfico de dispersão, não há muitas outras opções, portanto, o uso de bolhas dimensionadas em gráficos de dispersão é um método aceitável. Ao usar bolhas dimensionadas, esteja atento à perda de precisão de visualização com a terceira variável.
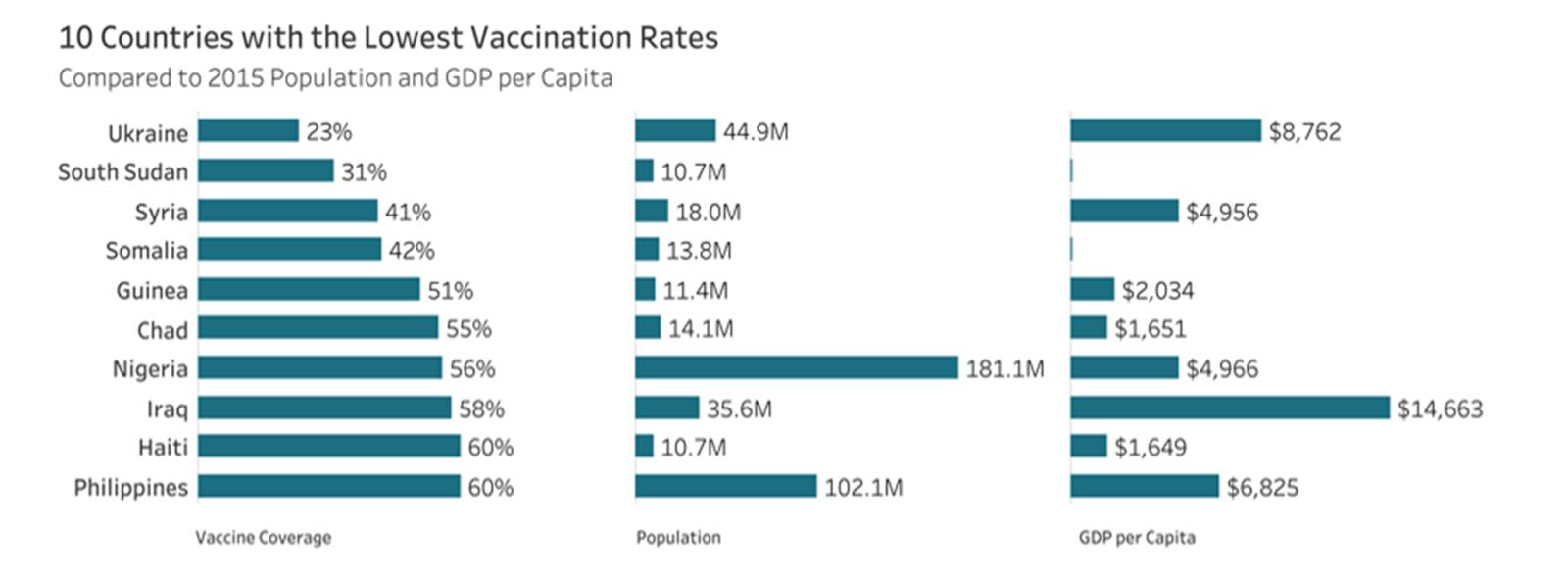
Em situações em que não existem muitos pontos de dados ou em que você só pretende comparar o conjunto de valores superior ou inferior de uma das variáveis, os gráficos de barras podem ser úteis sob a forma de uma Table Lens. A Table Lens permite que três ou mais variáveis quantitativas sejam comparadas com uma variável qualitativa (categórica) comum.
O exemplo mostra as mesmas variáveis que o gráfico de dispersão de bolhas dimensionadas mostrado acima, exceto que mostra apenas os 10 países com a cobertura de vacinação mais baixa. A Table Lens também permite a comparação entre várias métricas ou dentro de uma métrica individual.
Recursos
- Site do Financial Times: Gráficos que funcionam: Guia de vocabulário visual do Financial Times
- Trailhead: Distribuições de dados
- Trailhead: Correlação e regressão
- Livro: Introdução à estatística. Online Statistics Education: An Interactive Multimedia Course of Study, 2020 (Formação em Estatística online: um curso multimídia interativo, 2020), de David M. Lane.
- Publicação do blog Sellers Dorsey: A Histogram and Frequency Polygon Walk Into a Bar (Um histograma e um polígono de frequências na barra)