편차, 분포, 상관 비교 수행

학습 목표

이 유닛을 완료하면 다음을 수행할 수 있습니다.

• 편차, 분포 및 상관 비교를 알아봅니다.
  
• 차트로 비교를 수행하는 모범 사례를 이해합니다.
  

편차

편차 비교는 값이 기준값(때로는 평균 또는 임곗값)과 다른 정도에 초점을 맞춥니다.

양방향 막대 차트

이 예에서는 막대의 길이로 중심 값인 0으로부터의 거리를 표시하여 손익 금액을 보여줍니다. 이를 통해 수익성이 낮은 항목과 지역을 빠르게 확인할 수 있습니다.

선 차트

이전에 선 차트가 시간에 따른 값의 변화를 표시하는 탁월한 방법이라는 것을 배웠습니다. 마찬가지로 선 차트는 시간 경과에 따른 편차를 표시하려는 경우에도 유용합니다. 다음 예에서는 2015년과 2016년 월별 응급실 환자 수의 전년 대비 변화율을 보여 줍니다. 6월에 환자 수가 전년 대비 가장 많이 증가한 것을 볼 수 있습니다.

분포

분포는 가능한 모든 데이터 값과 발생 빈도(카운트)를 보여줍니다. 다시 말해, 분포는 데이터 집합에서 각 데이터 값이 몇 번 발생하는지를 나타냅니다.

히스토그램

휴대폰에서 매핑 앱을 사용하여 자주 가는 식당이 언제 가장 바쁜지 알아본 적이 있나요? 붐비는 시간을 보여주는 그래프를 본 적이 있을 것입니다. 이 그래프를 히스토그램이라고 합니다. 그래프의 최고점이 가장 바쁜 시간을 나타냅니다.

히스토그램은 막대 차트와 비슷하지만 수량 값을 동일한 크기의 범위, 즉 빈(bin)으로 그룹화하고 각 빈에 있는 값의 개수를 계산하여 히스토그램으로 표시합니다. Tableau와 같은 프로그램을 사용하는 경우 자동으로 빈 크기가 파악되며 각 빈에 있는 값의 빈도(또는 개수)가 제공됩니다.

다음 예에서 히스토그램은 전체 데이터 집합의 주택 판매 가격 값에 대해 자세한 보기를 제공합니다. 대부분의 주택이 $100,000에서 $200,000 사이의 값에 판매되고 있음을 알 수 있습니다. 또한 히스토그램을 보면 대부분의 주택에 비해 가격이 더 높은 주택이 몇 개 있다는 것도 파악할 수 있습니다.

분포는 때때로 개수나 빈도 대신 백분율로 표시될 수 있습니다.

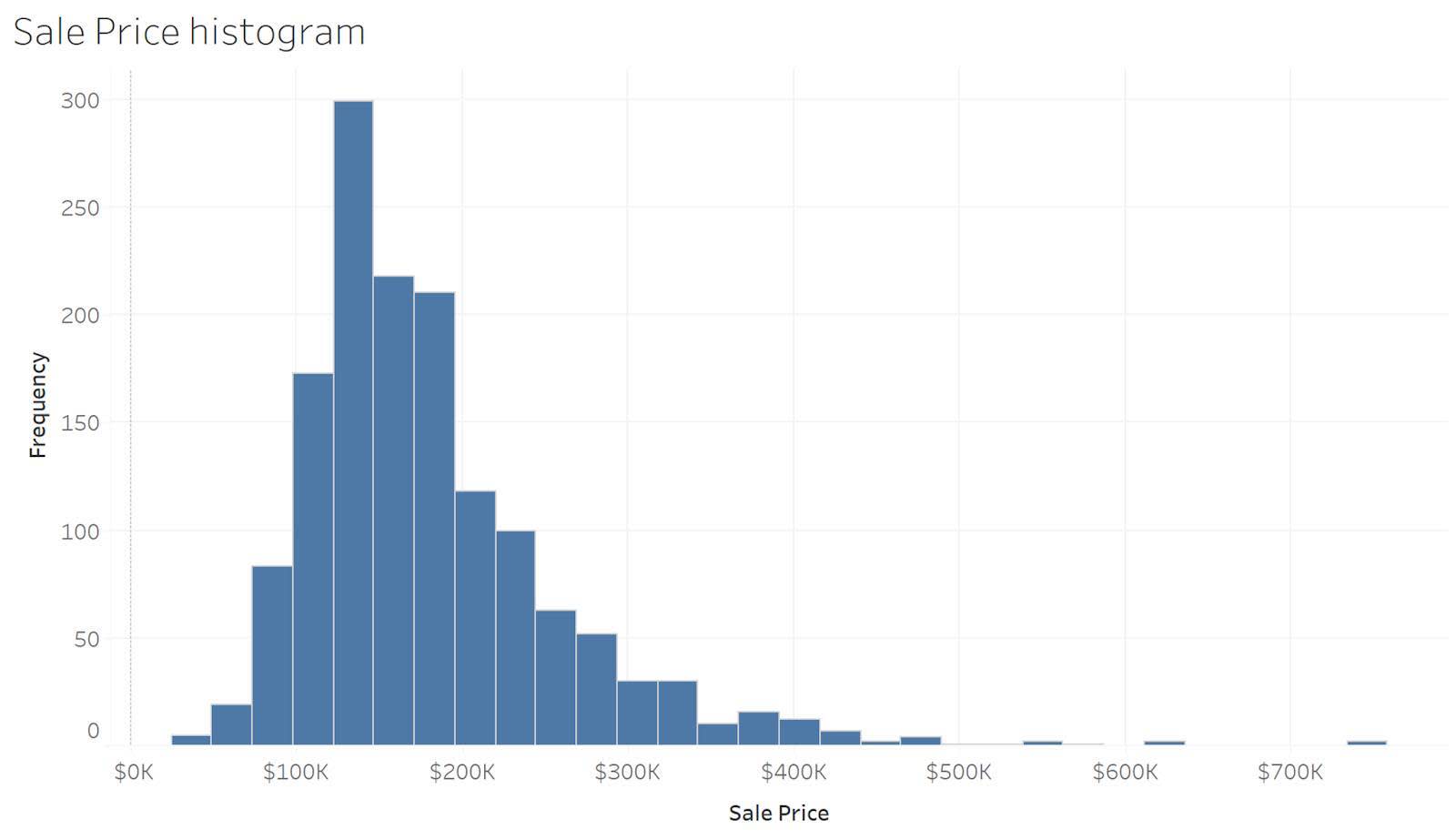
빈도 다각형

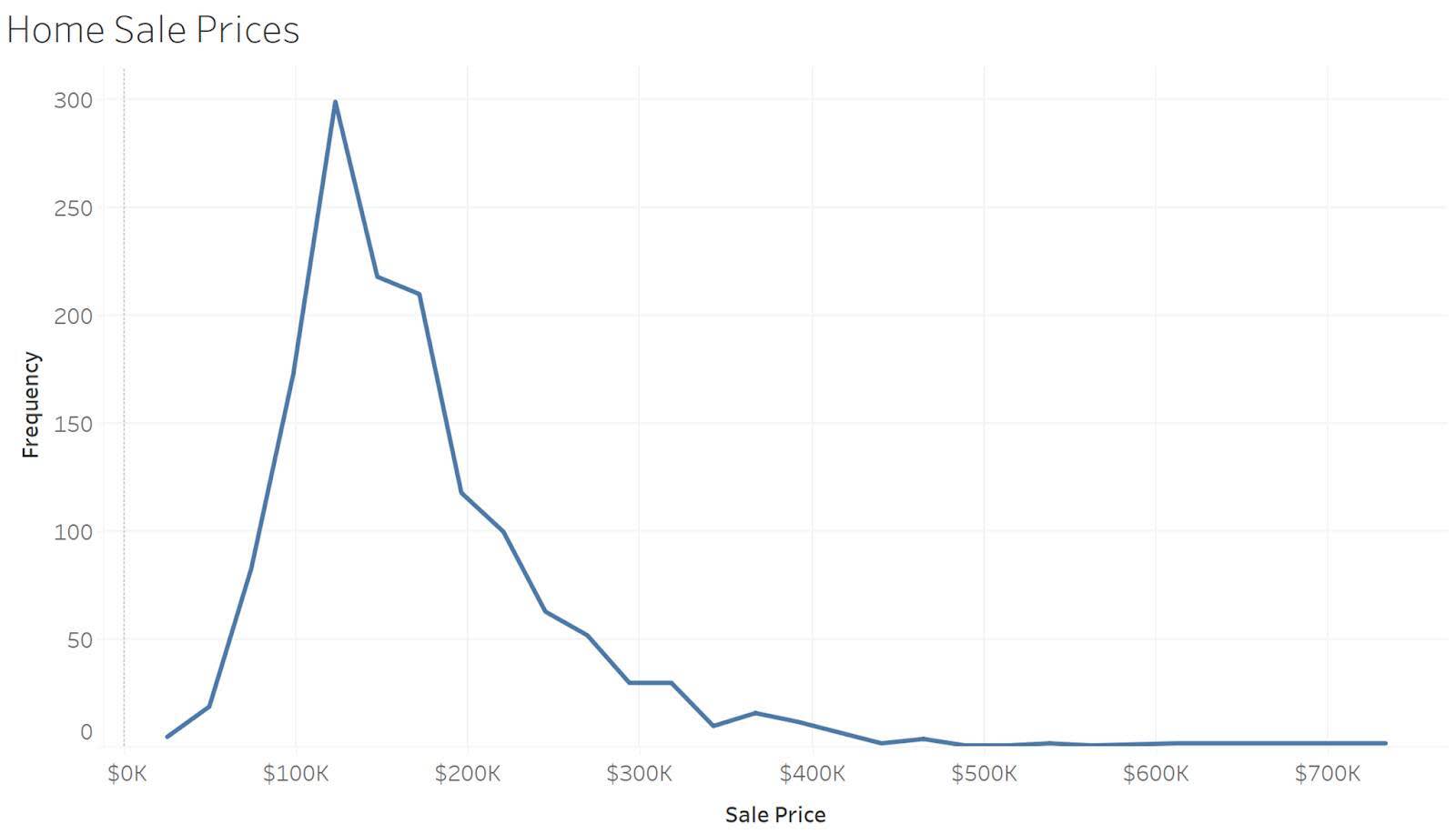
빈도 다각형은 히스토그램과 유사하지만, 선을 사용하여 빈도 수를 연결한다는 점에서 차이가 있습니다. 다음 예는 위의 히스토그램과 동일한 데이터를 보여주지만, 각 빈의 개수가 선으로 연결되어 있다는 점이 다릅니다. 선은 보기에 더 깔끔하고 단순한 편입니다.

동일한 그래프에 두 개 이상의 분포를 표시하려면 히스토그램 대신 빈도 다각형을 사용하세요.

스트립 플롯

스트립 플롯은 각 데이터 값에 대한 점을 한 줄로 표시하며 히스토그램이나 빈도 다각형보다 훨씬 적은 공간을 차지합니다. 스트립 플롯을 사용하면 효율적인 방식으로 분포의 범위와 값의 클러스터링 여부를 표시할 수 있습니다. 다만 여러 값이 동일하거나 서로 매우 가까운 경우 서로 겹쳐서 그려지기 때문에 데이터에서 자주 발생하는 값을 구분하기는 어렵습니다.

히스토그램과 동일한 데이터를 사용하는 다음 예에서 스트립 플롯을 사용하면, 단일 고가 주택은 쉽게 볼 수 있지만 가장 빈도가 높은 판매 가격을 보기는 어렵다는 것을 알 수 있습니다. 따라서 데이터 집합이 작은 경우에 스트립 플롯을 사용하는 것이 가장 좋습니다.

스트립 플롯의 점을 투명하게 만들면 여러 점을 더 어둡게 표시할 수 있으며 단일 값과 여러 유사한 값을 구분할 수 있습니다.

상자 플롯

상자 플롯은 히스토그램보다 더 간결한 형태로 분포를 표시합니다. 또한 여러 분포를 비교할 때 카테고리 간의 분포를 효율적으로 비교할 수 있는 방법을 제공합니다. 상자 플롯의 상자는 데이터의 중간 50%, 즉 25~75번째 백분위수를 표시하며 중앙값, 즉 50번째 백분위수를 나타내는 선을 포함합니다.

하지만 그 바깥에 있는 데이터는 어떨까요? 여기에서 수염이 들어오고, 상자 외부에 플로팅되며 수염은 수평 스트로크로 끝나는 수직선입니다. 이는 데이터의 중간 50%(상자)에 속하지 않는 값에 대한 인사이트를 제공하고 이상값을 구분할 수 있는 경계를 제공합니다. 이상점은 비정형 및 드문 관찰, 또는 분포의 중심으로부터 극단적인 편차를 갖는 값으로 이해될 수 있습니다.

상자 플롯에서는 여러 방법으로 잠재적 이상값이 있을 수 있는 경계를 계산할 수 있습니다. 일부 프로그램에서는 극단적인 이상값이 일반적인 경계에서 멀리 떨어져 있는 경우 다른 기호로 해당 값을 표시할 수 있습니다.

다음 예는 다양한 건물 유형에 대한 주택 판매 가격의 분포를 비교한 것입니다. 이상값으로 보이는 여러 고가 주택을 포함하여 다른 건물 유형보다 단독 주택이 훨씬 더 넓은 범위의 값을 보이는 것을 알 수 있습니다.

이 상자 플롯 예시에는 각 개별 값을 표시하는 수직 스트립 플롯도 포함되어 있습니다. 따라서 모든 데이터 포인트와 분포에 대한 세부 정보를 동일한 시각적 보기에서 확인할 수 있습니다. 상자 플롯을 읽는 방법을 익히기까지는 약간의 시간이 필요할 수 있지만, 상자 플롯은 많은 공간을 사용하지 않고도 분포에 대한 많은 정보를 전달하는 좋은 방법입니다.

분포에 대해 자세히 알아보려면 Trailhead의 데이터 분포 모듈을 확인하세요.

상관관계

상관 비교는 정량적 변수 간의 관계를 분석합니다. 이를 사용하면 ‘한 변수가 다른 변수에 따라 증가하거나 감소하는가?’와 같은 질문에 대한 답을 찾을 수 있습니다.

통계에서 상관관계라는 용어는 특정한 의미를 가질 수 있습니다. 예를 들어, 상관 계수에 대해 이야기할 때 이는 일반적으로 선형인 정량적 변수 간의 특정 관계 유형을 의미합니다. 상관관계와 회귀 모듈에서는 상관관계 및 회귀 분석을 수행하는 방법을 배웁니다.

산점도

산점도는 두 정량 변수 간의 관계를 표시하는 데 사용되며, 한 변수는 X축에, 다른 변수는 Y축에 표시됩니다. 산점도는 변수 간에 관계가 있는지 여부를 보여줄 수 있습니다. 예를 들어, 한 변수가 다른 변수와 '같은 방향'으로 이동하는지, 선형 또는 다른 패턴과 같은 관계 유형이 존재하는지 등을 확인할 수 있습니다.

산점도를 보면 이상값을 파악하는 데에도 도움이 될 수 있습니다. 다음 예는 주택 판매 가격과 거주 면적 간의 관계를 보여줍니다. 산점도의 각 점은 주택 판매 가격을 Y축으로, 주거 면적을 X축으로 사용하여 그래프에 배치된 단일 주택을 나타냅니다.

산점도는 두 변수 간의 관계를 보여줄 수는 있지만, 한 변수가 다른 변수에 영향을 미친다는 것을 증명하지는 못합니다. “상관관계가 인과 관계를 증명하지 못한다"는 말을 들어보셨을 것입니다. 변수 간의 관계에는 여러 가지 이유가 있을 수 있습니다.

추세선

산점도의 추세선은 관계의 전반적인 패턴을 확인하고 데이터의 전체적인 모양을 요약하는 데 도움이 됩니다. 주택 판매 가격과 면적의 예에서 선형 추세선을 사용하면 관계의 전반적인 패턴을 볼 수 있습니다.

모든 관계가 선형인 것은 아닙니다. 특정 관계가 곡선으로 표시되는 경우, 선형 대신 지수나 로그와 같은 추세선을 사용할 수 있습니다.

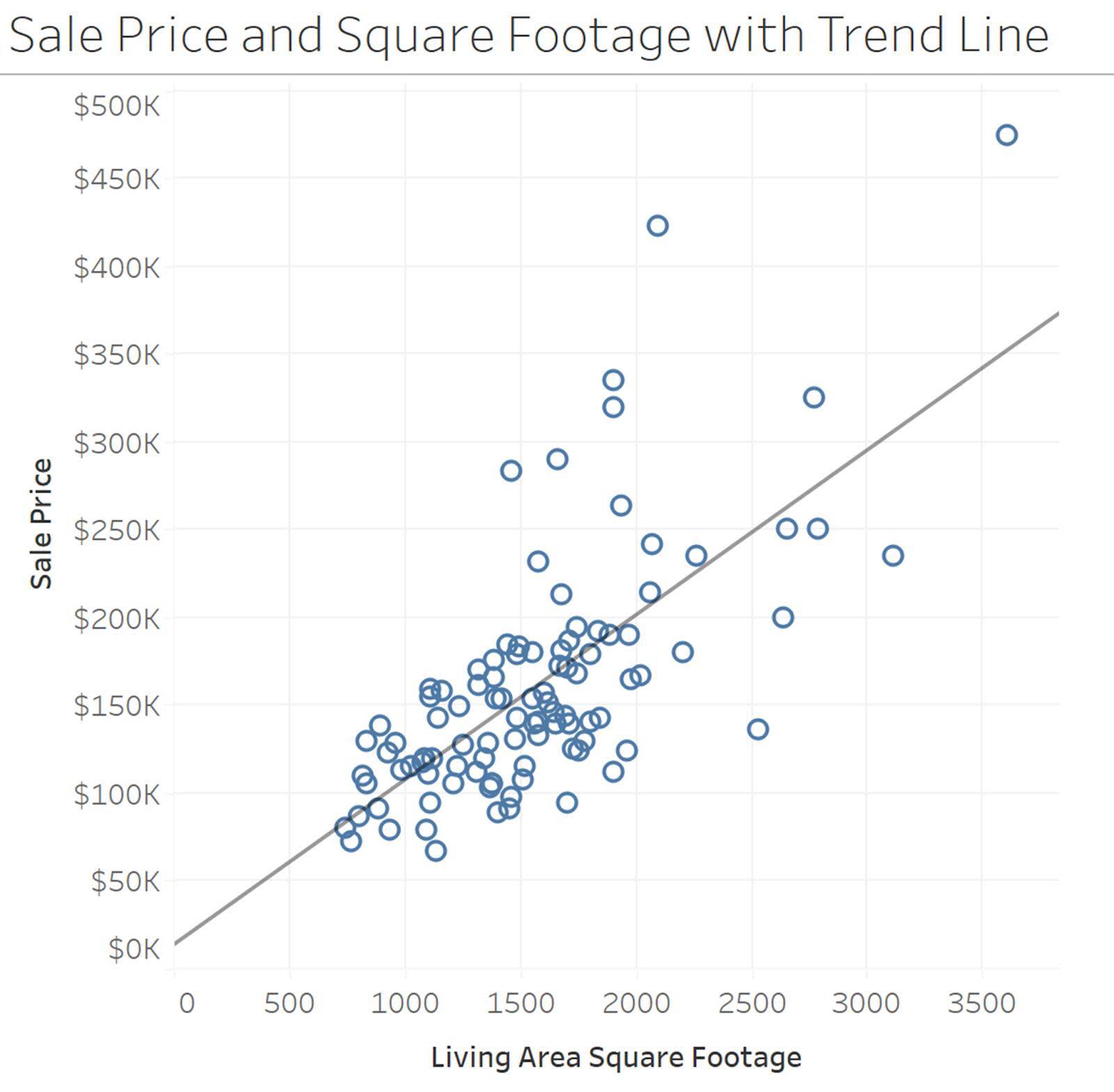
상관관계 및 선형 회귀선을 만드는 방법을 자세히 알아보려면 Trailhead의 상관관계와 회귀 모듈을 참고하세요.

다양한 크기의 거품 산점도 및 테이블 렌즈

이전 산점도에서는 두 개의 정량적 변수 사이의 관계를 보여주며 하나는 X축에, 다른 변수는 Y축에 표시했습니다. 하지만 두 개 이상의 정량적 변수를 비교할 때는 어떻게 해야 할까요? 다른 특성인 크기를 사용하여 산점도에 세 번째 변수를 추가할 수 있습니다.

다음 예에서는 1인당 GDP와 백신 접종률을 각각 X축과 Y축에 표시하며, 각 거품의 크기는 인구 규모를 나타냅니다.

이 모듈의 앞부분에서는 차트를 보는 사람들이 길이와 같은 기타 특성만큼 정량적 크기의 차이를 정확하게 인식하기 어렵다는 내용을 배웠습니다. 산점도에 세 번째 정량적 변수를 추가할 경우 다른 옵션이 많지 않으므로 산점도에 다양한 크기의 거품을 사용할 수 있습니다. 다양한 크기의 거품을 사용할 때는 세 번째 변수로 인해 보기의 정확도가 떨어질 수 있다는 점에 유의하세요.

데이터 포인트가 많지 않거나 변수 값의 상위 또는 하위 집합만 비교하려는 경우에는 테이블 렌즈 형식의 막대형 차트가 유용할 수 있습니다. 테이블 렌즈를 사용하면 공통의 정성적(범주형) 변수에 대해 세 개 이상의 정량적 변수를 비교할 수 있습니다.

이 예는 위에 표시된 다양한 크기의 거품 산점도와 동일한 변수를 보여주지만 백신 접종률이 가장 낮은 10개 국가만 표시합니다. 또한 테이블 렌즈를 사용하면 여러 지표 또는 개별 지표 내에서도 비교가 가능합니다.

리소스

• Financial Times 웹 사이트: Charts that work: FT visual vocabulary guide(유용한 차트: FT 시각 자료 용어 가이드)
• Trailhead: 데이터 분포
• Trailhead: 상관관계와 회귀
• 책: Introduction to Statistics. Online Statistics Education: An Interactive Multimedia Course of Study(통계 입문. 온라인 통계 교육: 대화형 멀티미디어 연구 과정), 2020, David M. Lane.
• Sellers Dorsey 블로그 포스트: A Histogram and Frequency Polygon Walk Into a Bar(막대형 차트에 히스토그램 및 빈도 다각형 추가하기)