집계 살펴보기
학습 목표
이 유닛을 완료하면 다음을 수행할 수 있습니다.
- 집계를 정의할 수 있습니다.
- 다양한 집계 유형을 적용할 수 있습니다.
집계란 무엇입니까?
집계는 정량적 데이터의 컬렉션을 의미하며 데이터의 주요 추세를 나타낼 수 있습니다. 예를 들어 특정 캠핑장에 대한 모든 웹 검색을 합산하거나 한 도시의 모든 임금 근로자의 평균 소득을 계산하는 것과 같습니다.
많은 분석 도구에서 정량적 변수는 기본적으로 집계되지만, 데이터 원본의 모든 행에 있는 모든 값에 대한 데이터 포인트를 표시하려면 분배(범주별 분류)하면 됩니다.
다음은 몇 가지 일반적인 집계입니다.
집계 |
설명 |
예: 3, 3, 6 |
|---|---|---|
합계 |
값의 산술 합계 |
3 + 3 + 6 = 12 합계 = 12 |
평균 |
값의 산술 평균(즉, 합계를 값의 개수로 나눈 값) |
3 + 3 + 6 = 12 12/3 = 4 평균 = 4 |
중앙값 |
최소값에서 최대값(또는 최대값에서 최소값)으로 정렬된 값 목록의 중간값 |
3, 3, 6 중앙값 = 3 |
최소값 |
가장 작은 값 |
3, 3, 6 최소값 = 3 |
최대값 |
가장 큰 값 |
3, 3, 6
최대값 = 6 |
개수 |
값의 수(데이터 테이블의 행 또는 레코드 수) |
세 개의 값이 있습니다.
개수 = 3 |
|
고유값 개수 (또는 유일한 값 개수) |
고유값의 수로, 각 유일한 값이 한 번만 계산됨(데이터 테이블의 경우 레코드의 고유한 행 개수를 말함) |
유일한 값(3과 6)이 두 개 있습니다.
고유값 개수(또는 유일한 값 개수) = 2 |
집계의 예
집계의 몇 가지 예와 이러한 집계가 데이터 분석에 미치는 영향을 살펴보겠습니다. 온라인 어휘 테스트와 관련된 설문 조사 데이터를 사용하겠습니다. 각 참가자는 온라인 어휘 퀴즈를 풀고 자신에 대한 인구 통계학적 질문에 답했습니다.
집계된 정량적 변수를 사용하여 시각화 보기
다음 시각화에서 Age(연령) 정량적 변수를 살펴보세요. Sum(합계)의 집계는 총 420,085년에 대한 Age(연령) 변수의 모든 값을 합산합니다.

위 차트에서는 하나의 막대를 사용하여 데이터 세트의 모든 데이터(12,168행)를 하나의 숫자로 요약합니다.
이 Sum of Age(연령 합계)는 최종 학력별로 분류될 수 있으며, 그 결과 막대로 각 학력 수준의 총 연령을 보여주게 됩니다. (이러한 각 값을 합산하면 막대 한 개의 합계와 같습니다. 116,602 + 160,542 + 120,351 + 22,092 + 498 = 420,085.)

유의 사항: 116,602년이라는 연령은 유의미하지 않으므로 이 경우 Sum(합계)은 집계로 적절하지 않습니다. 이 예의 age(연령)와 같은 일부 변수의 경우 Sum(합계) 집계를 사용하면 데이터를 유용하거나 적절하게 표현할 수 없습니다. (sum(합계)이 집계로 적절한 경우도 있습니다.) 시각화를 생성하거나 볼 때 분석 및 차트에 사용되는 집계에 유의하는 것이 중요합니다.
기본 데이터 보기
합산되는 값을 더 잘 이해하기 위해 원시 데이터를 살펴보겠습니다. 행 수준 데이터를 검토해 보면 각 참가자와 해당 교육 수준 및 연령에 대한 행을 확인할 수 있습니다.
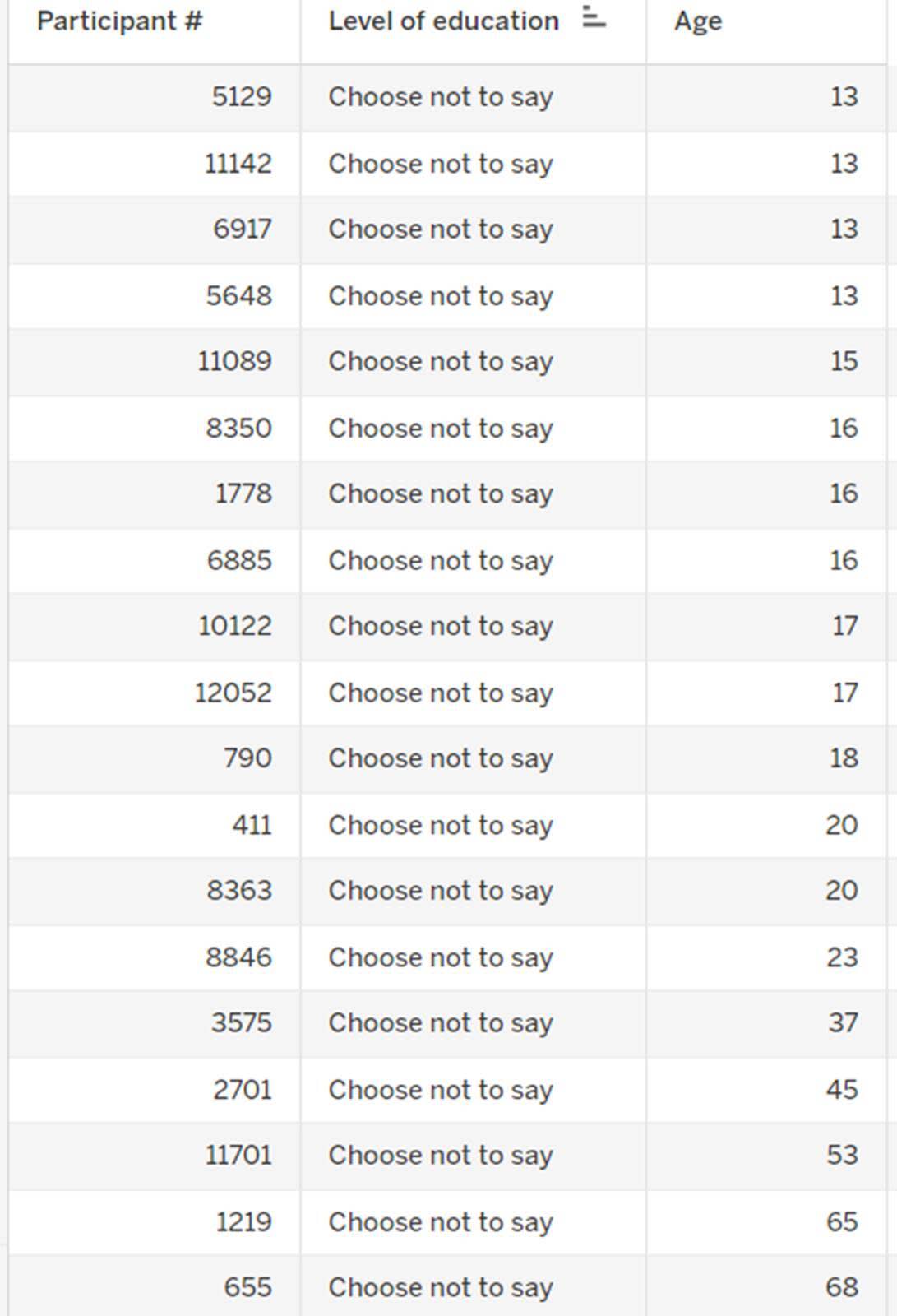
Choose not to say(응답을 원하지 않음)에 해당하는 학력 수준을 살펴보면 연령 합계는 498입니다.
13 + 13 + 13 + 13 + 15 + 16 + 16 + 16 + 17 + 17 + 18 + 20 + 20 + 23 + 37 + 45 + 53 + 65 + 68 = 498년
평균 집계의 영향 보기
이전과 동일한 바 차트를 살펴보되, 이번에는 집계를 평균으로 변경해 보겠습니다. 이제 모든 연령을 합산하여 해당 값을 표시하지 않습니다. 대신 막대의 높이가 산술 평균을 가리키게 됩니다. 각 학력 수준의 경우 모든 연령을 합산하여 값의 개수로 나눕니다.

Choose not to say(응답을 원하지 않음)에 해당하는 학력 수준(하늘색으로 표시됨)의 평균은 26.21세입니다.
13 + 13 + 13 + 13 + 15 + 16 + 16 + 16 + 17 + 17 + 18 + 20 + 20 + 23 + 37 + 45 + 53 + 65 + 68 = 498
498 ÷ 19 = 26.21
이제 숫자가 한 사람의 현실적인 연령으로 나타납니다(약 20~43세). 그리고 평균적으로 젊은 응답자들은 학력 수준이 낮습니다.
중앙값 집계의 영향 보기
Age(연령)가 데이터 세트에서 중앙값(또는 중간값)으로 집계되는 경우를 살펴보겠습니다. 평균은 극값의 영향을 받아 늘어나거나 편향될 수 있습니다. 예를 들어 103세인 한 사람이 퀴즈를 푼 경우 이 응답자의 연령으로 인해 해당 교육 범주에 속하는 참가자의 연령이 전반적으로 높아질 수 있습니다. 극값으로 인한 편향 문제를 방지하기 위해 MEDIAN(중앙값) 집계는 모든 값의 순위를 순서대로(최대값에서 최소값 또는 최소값에서 최대값으로) 지정하고 중간값을 반환합니다.

Choose Not to Say(응답을 원하지 않음)에 해당하는 학력 수준(하늘색으로 표시됨)의 중앙값 연령은 17세입니다.
13 , 13 , 13 , 13 , 15 , 16 , 16 , 16 , 17 , 17 , 18 , 20 , 20 , 23 , 37 , 45 , 53 , 65 , 68
이 차트에서는 중앙값 연령이 조금 더 낮은 것을 확인할 수 있습니다. 퀴즈 참여에 연령 제한은 없으나 참가자가 최소 13세 이상이어야 하기 때문에 더 낮은 중앙값이 예상될 수 있습니다. 즉, 평균을 낮출 수 있는 젊은 연령의 극값은 존재하지 않습니다. 그리고 전반적인 추세는 여전히 학력 수준이 높을수록 참가자의 연령이 높은 것으로 나타납니다.
최소값 및 최대값 집계의 영향 보기
최소값 집계는 선택한 데이터에서 가장 작은 값을 반환하고, 최대값 집계는 가장 큰 값을 반환합니다.

Choose Not to Say(응답을 원하지 않음)에 해당하는 학력 수준(하늘색으로 표시됨)의 최소값 연령은 13세입니다.
13 , 13 , 13 , 13 , 15 , 16 , 16 , 16 , 17, 17 , 18 , 20 , 20 , 23 , 37 , 45 , 53 , 65 , 68
Choose Not to Say(응답을 원하지 않음)에 해당하는 학력 수준(하늘색으로 표시됨)의 최대값 연령은 68세입니다.
13 , 13 , 13 , 13 , 15 , 16 , 16 , 16 , 17, 17 , 18 , 20 , 20 , 23 , 37 , 45 , 53 , 65 , 68
개수 집계의 영향 보기
이제 Age(연령)가 개수로 집계되면 어떤 결과가 발생하는지 살펴보겠습니다. 개수는 선택한 범주에 대한 데이터의 값 개수를 반환합니다. 즉, 이제 연령이 아닌 참가자 수를 살펴보게 됩니다.
Choose Not to Say(응답을 원하지 않음)에 해당하는 학력 수준을 살펴보면 개수는 19이며, 고유값 개수는 12입니다. 참가자 4명이 13세, 2명이 16세, 2명이 20세였기 때문에 고유값 개수는 12입니다. 고유값 개수 집계는 유일한 값만 계산하기 때문에 12, 13, 20은 한 번만 계산됩니다.
|
개수는 19입니다 13 13 13 13 15 16 16 16 17 17 18 20 20 23 37 45 53 65 68 |
반면에 고유값 개수는 12입니다 13 15 16 17 18 20 23 37 45 53 65 68 |
|---|
개수로 미루어 보아 학력 수준을 밝히지 않은 참가자는 거의 없음을 알 수 있습니다.
분배의 예
처음 살펴본 차트에서는 데이터를 완전히 집계하여 전체 Sum(합계)이라는 하나의 값만 볼 수 있었습니다. 그런 다음 전체 데이터 세트를 Level of Education(학력 수준)별로 분배하여 각 학력 수준에 해당하는 연령 합계를 분류했습니다. 이제 데이터 세트에 있는 전 연령의 합계(또는 평균 또는 최소값)는 살펴보지 않습니다. 그 대신 각 막대는 각 학력 수준의 범주로 집계됩니다. 데이터는 계속 집계되지만 그 수준이 더 상세합니다.
|
|
|---|
이제 원본 데이터를 다시 살펴보겠습니다.
각 행은 참가자를 나타냅니다. 집계된 값 대신 각 참가자의 연령을 확인하려면 데이터를 완전히 분배하거나 데이터 세트의 각 포인트를 플롯으로 그리면 됩니다.
데이터 분배의 영향 보기

이 차트는 지터를 사용하여 데이터 포인트 또는 표식을 분산합니다. 지터란 데이터 밀도를 나타낼 수 있도록 간격이 없는 축(이 경우 x축)을 따라 표식을 무작위로 배치하는 것을 말합니다. 지터가 없는 경우 표식은 학력 수준별로 하나의 수직선에 모두 쌓이게 됩니다. 지터 플롯에서 표식의 수평 위치는 무작위이며 특별한 의미를 전달하지는 않습니다.
이 시각화에서는 연령이 낮을수록 참가자가 많고, 연령이 높아질수록 참가자가 적음을 확인할 수 있습니다. 또한 Less than high school(고등학교 미만) 범주에는 나이가 많은 참가자가 일부 있기도 하지만, 대다수는 20세 미만의 꽤 젊은 참가자임을 알 수 있습니다. High school(고등학교) 범주에는 20대 초반의 연령이 가장 많은데, 현재 이들이 대학생임을 추정해 볼 수 있습니다. 석사 학위를 가진 20세 미만의 참가자도 거의 없습니다. 연령과 학력 수준에 대해 우리가 알고 있는 정보를 고려해 보면 분배된 데이터는 현실적인 기대치와 밀접하게 일치합니다.
연습하기
과제: 다음 표에는 주간 신문 독자 수에 대한 데이터가 세 개의 행으로 주어져 있습니다.
이름 |
주간 신문 읽기 |
|---|---|
브루클린 |
2 |
모건 |
3 |
바이다 |
7 |
Newspapers read per week(주간 신문 읽기) 변수(2, 3, 7)의 값은 합계, 평균, 중앙값, 최소값, 최대값, 개수로 어떻게 집계되나요? 잠시 생각해 본 후 아래 주어진 대화형 플래시 카드를 사용하여 답을 확인하세요.
각 카드의 집계 유형을 읽고 해당 집계 값에 대해 생각해 본 후 카드를 클릭하여 정답을 표시하세요. 오른쪽 화살표를 클릭하면 다음 카드로 이동하고, 왼쪽 화살표를 클릭하면 이전 카드로 돌아갑니다.
집계가 데이터에 미치는 영향과 데이터 분배 효과에 대해 알아보았습니다. 다음 유닛에서는 세분화에 대해 알아보고 해당 개념에 대해 숙지할 수 있습니다.
리소스


