確率を推定する
学習の目的
この単元を完了すると、次のことができるようになります。
- 連続分布について説明する。
- 正規分布の特徴について説明する。
はじめに
「データの分布」モジュールでは、ヒストグラムを使うことで連続値の分布をグラフ化できることを説明しました。 ここでは、連続分布の概念について見ていきましょう。
この単元では、計算に使用される式の詳細には触れませんが、こういった概念について一般的な知識を得ておくと、データを考察、理解、伝えていくうえで役に立つでしょう。
密度曲線
「データの分布」モジュールでは、連続変数の有限な標本 (サンプル) の分布をヒストグラムで表す方法について説明しました。 ヒストグラムのそれぞれの棒の高さは、そのビン内の値の頻度に比例します。つまり、棒が高いほど、標本 (サンプル) のデータポイントがそのビン内に出現する頻度が高いことを意味します。
たとえば、上記のヒストグラムは、40 人の身長 (インチ) の分布を示しています。明らかに、これは有限のデータポイントの標本 (サンプル) です。ですが、身長という連続変数が取り得る値をすべて考慮すると、ばらつきが大きくなる可能性があることがわかります。また、可能性のあるすべての身長値のビンを持つヒストグラムを作成している時間も十分にはありません。これは、どんな連続変数にも言えることです。
ヒストグラムを使用して連続変数の取り得る値をすべて表現する代わりに、連続分布を使用できます。連続分布は密度曲線とも呼ばれ、滑らかな曲線のように見えます。密度曲線が表すのは、特定の標本 (サンプル) に含まれる値だけではありません。取り得るすべての値と、その出現確率、つまり値がどのくらい発生するかも表しています。
ヒストグラムでは、棒の高さから、そのビン内で発生するデータポイントの数、つまり、そのビン内のデータポイントの頻度がわかります。ただし、連続分布の場合は、確率曲線の高さから同様の解釈をすることはできません。
身長に関するあらゆる値が含まれたデータを想像してみてください。そのなかで、身長が 61 インチちょうどの人がいる確率を尋ねても、あまり意味がありません。なぜなら無限の値がある中で、61 インチちょうどの値について尋ねることは、61.002 インチや 60.9997 インチちょうどの人がいる確率について尋ねることと同じぐらい恣意的であるからです。
そこで、代わりに区間内の確率を見ることにします。この確立は、その区間内の曲線の下の部分の面積に相当します。
そうすると曲線の下の面積の合計は 1、つまり 100% となります。これは、取り得るすべての値が曲線のどこかしらに収まる確率が 100% だからです
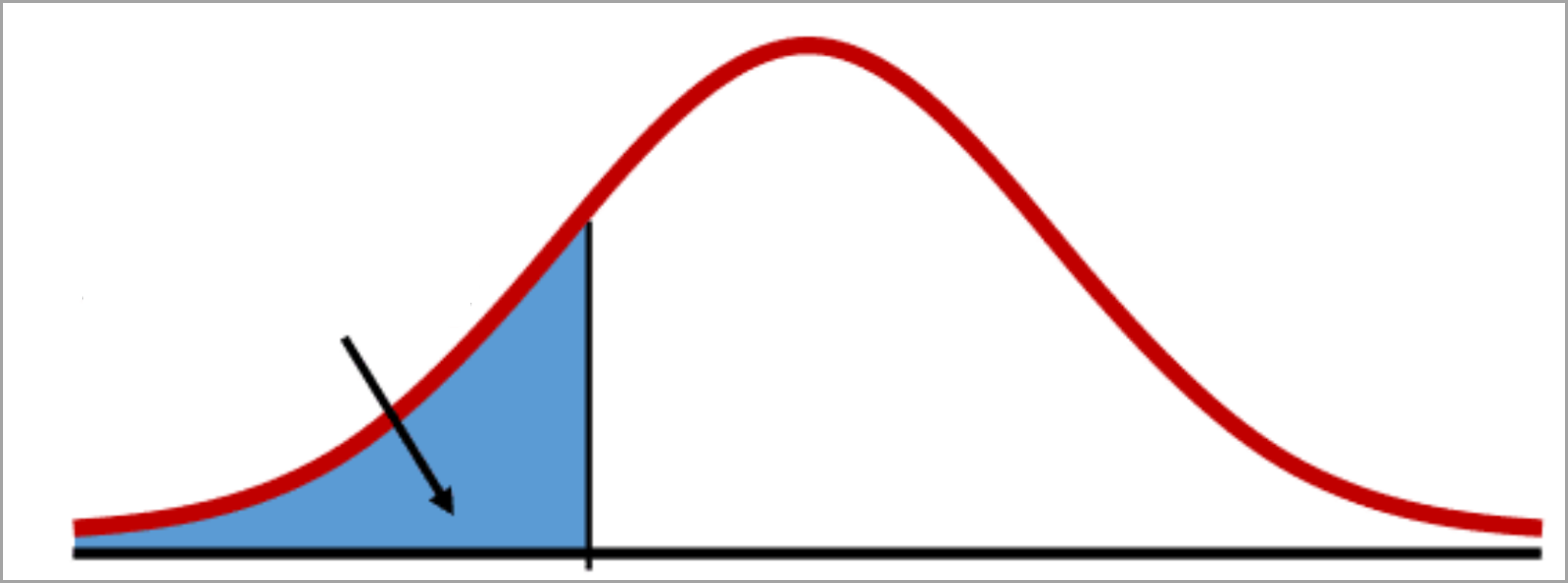
ここで、密度曲線について考える上で留意すべきいくつかの概念をまとめました。
- 曲線の下の合計面積は 100% または 1 である。
- このような曲線は可能性のあるすべてのデータポイントを一度に表現する連続分布である。
- Y 軸は確率密度を表し、X 軸上の対応するポイントの近くで値が得られる可能性を示している。
正規分布
次は、特殊な密度曲線である、正規分布または正規曲線に着目してみましょう。これは、左右対称の「釣鐘」の形をしています。
ヒストグラムでグラフ化された、連続変数の分布について説明した際、対称分布についても詳しく学びました。左右対称に分布したヒストグラムを半分に折り曲げると、2 つの面が完全に一致します。対称分布では、平均値と中央値が等しくなります。
対称分布と同様に、正規分布でも形は左右対称で、平均値と中央値も一致します。
正規分布の主な特徴は以下のとおりです。
- 平均値を中心として左右対称である。
- 平均値と中央値が等しい。
- 正規曲線の下の面積は 1.0 (100%) に等しい。
- 中心部分は密度が高く、裾部分は密度が低い。
- 平均と標準偏差という 2 つのパラメーターで定義される。
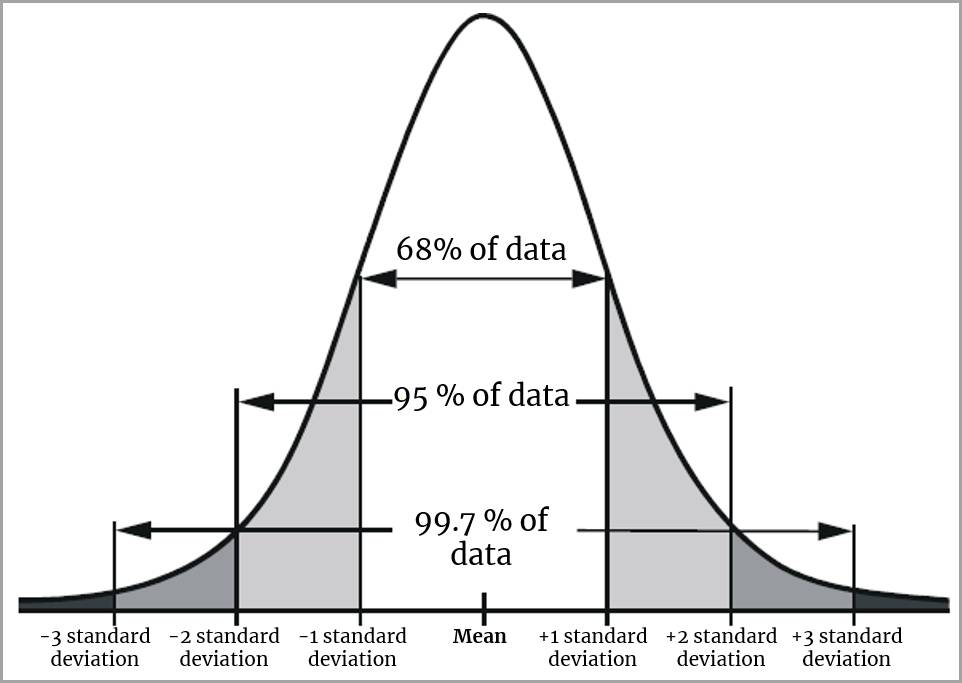
上の曲線で示されている正規分布を見てください。正規分布では、68% のデータが平均から +1/-1 標準偏差以内に収まり、95% のデータが平均から -2/+2 標準偏差以内に収まります。曲線の両側にある短い「裾」は、平均から -2/+2 標準偏差以内に収まらない値がごくわずか (5%) であることを示しています。
標準偏差が小さい正規分布は、標準偏差が大きい正規分布よりも、曲線の幅が狭く背が高くなります。
この図では、どちらの正規分布も平均値は 50 です。背の高い方の曲線の標準偏差は 5、背の低い方の曲線の標準偏差は 10 です。
正規分布の有用性
情報デザイナーである Alberto Cairo 教授は、その著書『The Truthful Art (真実を語るアート)』で、「自然界のいかなる現象も完全な正規分布に従うことはないが、多くの現象はそれに近似しているため、正規分布は統計学において主要なツールの 1 つとなっている。たとえ研究している現象が完全ではないにせよ、正規分布であることがわかっている場合は、どのようなケースやスコアの確率も十分な精度で推定することができる」と説明しています。つまり、正規曲線の特性を利用して、あるケースやスコアの確率をかなりの精度で合理的に推定することができるということです。
母集団全体を測定できることはまれであるため、多くの場合、母集団の推定は標本 (サンプル) から導き出されます。標本 (サンプル) が母集団を代表している場合、正規曲線は有用な推定ツールです。
信頼区間
正規曲線を使ってサンプルデータの確率を推定する場合は、信頼区間を使って誤差の許容範囲を算出することができます。
信頼区間は推論の一例です。推論とは、データの標本 (サンプル) に基づいて、母集団に関する結論を導き出すプロセスです。
信頼区間は、指定された割合の母平均を含んでいます。たとえば、信頼区間を 95% にする場合は、データの中の 95% の区間が真の平均を含んでいることを意味します。
95% の信頼区間は、95% のデータが平均から -2/+2 標準偏差以内に収まる正規分布を使って導かれます。
David M. Lane 氏によるオンラインのパブリックドメイン著作物『Introduction to Statistics (統計学入門)』の信頼区間に関する章から引用した例について考えてみましょう。
米国の 10 歳児の平均体重 (ポンド) を知りたいとします。当然、10 歳児全員の体重を測ることはできないので、代わりに標本 (サンプル) として 16 人の子供たちの体重を測り、平均体重が 90 ポンドであることがわかりました。この 90 という標本 (サンプル) 平均は母平均の推定値ですが、標本 (サンプル) 平均が母平均からどのくらい離れているかを明確に知る方法はありません。つまり、米国の 10 歳児の母集団全体の平均体重が 90 ± 5 ポンド以内に収まっていると確信してもよいのでしょうか? この答えを知ることはできないでしょう。
ですが、ある計算 (ここでは説明しません) を使用すれば、95% の信頼区間を算出することができます。この計算で、95% の信頼区間には、72.85 ～ 107.15 ポンドの平均体重が含まれることがわかりました。
つまり、米国の 10 歳児の母集団全体の平均体重が 72.85 ～ 107.15 ポンドに収まると信じるに十分な理由があることになります。なぜなら、標本 (サンプル) を繰り返し取得し、各標本 (サンプル) ごとに 95% の信頼区間を計算すると、取得回数の 95% の確率でその区間に真の平均が含まれることになるからです。
ただし、これは、取得回数の 5% で区間内に真の平均が含まれないことも同時に示しています。
不確実性が見られる実例
この単元で前述した Alberto Cairo 氏は、ハリケーンの進路を表すビジュアライゼーションにおいて、不確実性がどのように表現されているか (また、誤解されているか) の実例を説明したブログ記事を多数執筆しています。Alberto Cairo 氏の専門家向け Web サイトでは、2019 年に発生したカテゴリ 5 のハリケーン「ドリアン」の予測地図の誤解に関するブログ記事や、その他の関連記事にアクセスできます。
ここでは、正規曲線の特殊な形状を含め、連続分布について学習しました。次の単元では、データサンプルを使った仮説検定の概念について詳しく説明します。