偏差、分布、相関の比較を行う

学習の目的

この単元を完了すると、次のことができるようになります。

偏差、分布、相関の比較について説明する。
チャートを使用して比較を行う場合のベストプラクティスを理解する。

偏差

偏差の比較では、ベースライン値 (場合によっては平均値またはしきい値) から値がどれだけ離れているかに着目します。

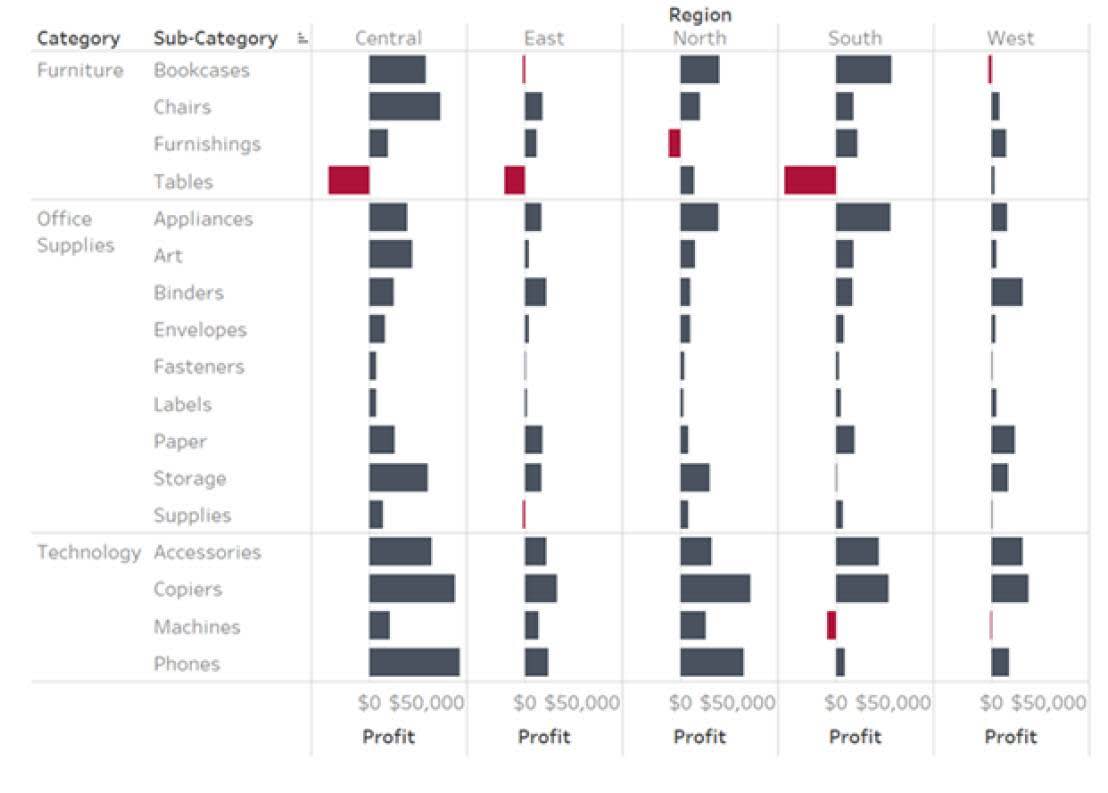
分散型棒グラフ

この例では、バーの長さが中心値である 0 からの距離を示し、利益または損失の金額を表します。このグラフから、利益を上げていない品目や地域がすぐにわかります。

商品カテゴリや地域ごとの利益と損失を示す分散型棒グラフ

折れ線グラフ

先ほど、値の経時的な変化を表す最適な方法の 1 つが折れ線グラフであると説明しました。同様に、経時的な偏差を示す場合も、折れ線グラフが最適なオプションです。次の例は、2023 年の各月を 2022 年と比較した緊急患者数の前年比変化率を示しています。6 月に患者の前年比増加率が最大になっていることがわかります。

2023 年の各月を 2022 年と比較した前年比変化率を示す折れ線グラフ

分布

分布は、すべての可能なデータ値とその出現頻度 (カウント) を表します。つまり、データセット内で各データ値が何回生じたかということです。

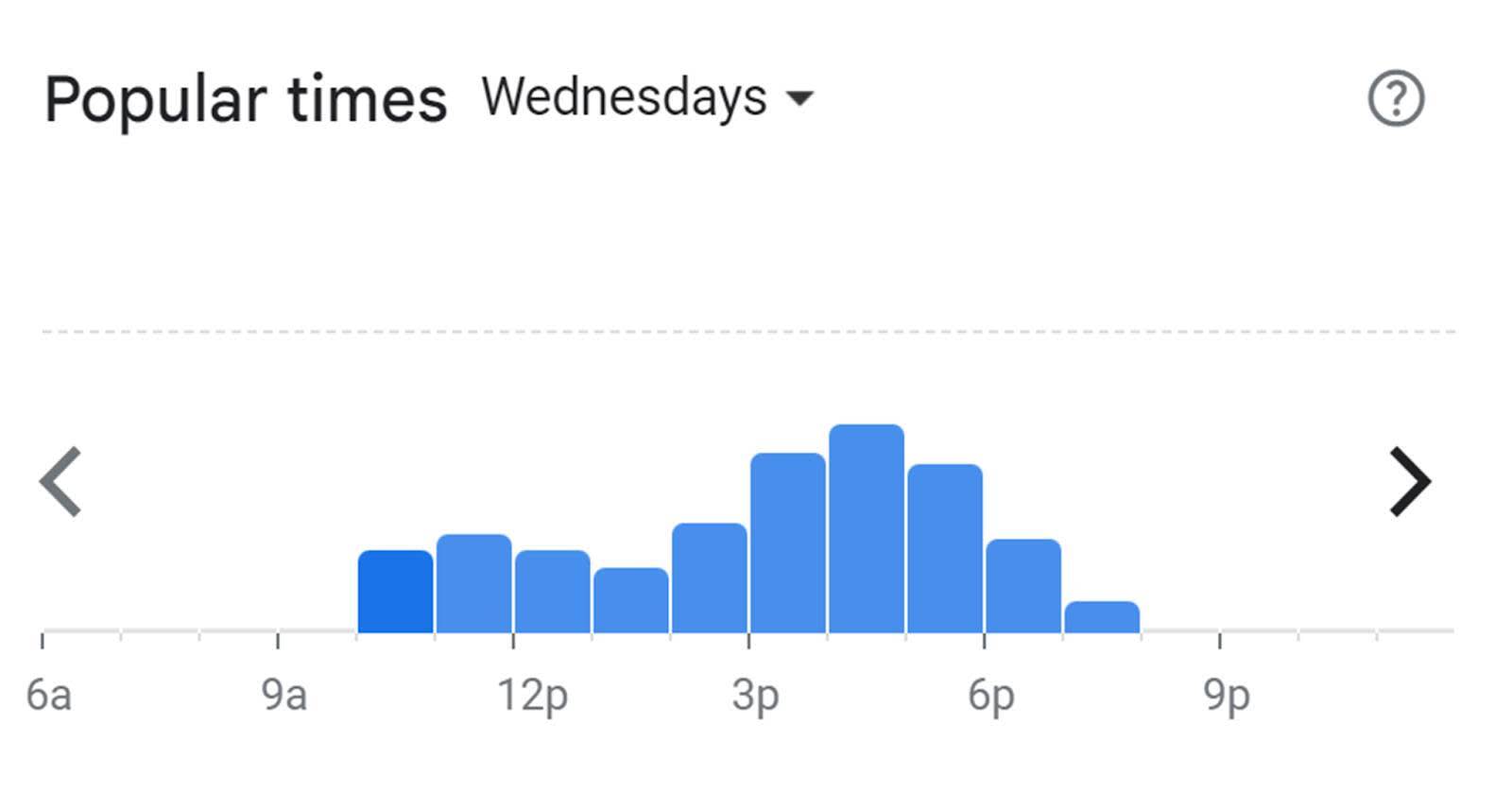
ヒストグラム

スマートフォンのマップアプリケーションを使用して、お気に入りのレストランが混雑している時間帯を調べたことはありませんか? 混雑時がグラフ表示されていることに気を留めたかもしれません。このグラフがヒストグラムで、最大値が最も混雑する時間帯です。

レストランが最も混雑する時間帯を示す Google マップのヒストグラム

棒グラフに似ていますが、この場合は量的な値を等間隔のビンに振り分け、ビンごとに値の数をカウントしてヒストグラムに表します。Tableau などのプログラムを使用すると、ビンのサイズが自動的に決定され、各ビンの値の頻度 (カウント) が示されます。

次の例は、データセット全体の住宅販売価格の値の詳細がヒストグラムに示されています。大半の住宅が 10 万～ 20 万ドルで販売されていることがわかります。このヒストグラムには、大多数の住宅と比較すると高額な住宅が数件あることも示されています。

住宅販売価格のヒストグラム

分布がカウントや頻度ではなく、割合で示されることもあります。

頻度ポリゴン

頻度ポリゴンはヒストグラムに似ていますが、頻度数が線で結ばれる点が異なります。次の例は、上記のヒストグラムと同じデータを示していますが、各ビンのカウントが線で結ばれています。線で示したほうがすっきりし、読み手にとって見やすくなります。

住宅販売価格の分布を示す頻度ポリゴン

同じグラフに複数の分布を示す場合は、ヒストグラムではなく、頻度ポリゴンを使用します。

ストリッププロット

ストリッププロットでは、各データ値を表すドットが一直線上に示されるため、ヒストグラムや頻度ポリゴンよりもはるかに少ないスペースに表示できます。ストリッププロットは、分布の範囲と値のクラスターの有無を示す効率的な手段です。ただし、同じ値、あるいは極めて近似の値が複数ある場合は重ねてプロットされるため、データ内で頻繁に発生する値を区別することが難しくなります。

次の例は、ヒストグラムと同じデータを使用しています。ストリッププロットでは、突出した高額の住宅を簡単に認識できる一方で、発生頻度が高い販売価格がわかりにくくなっています。したがって、データセットが小さい場合にストリッププロットを使用することをお勧めします。

住宅販売価格の分布を示すストリッププロット

ストリッププロットのドットを透明にすると、ドットが重なっている部分は色が濃くなるため、1 つの値と複数の近似した値を区別できるようになります。

箱ヒゲ図

箱ヒゲ図には、ヒストグラムよりもコンパクトな形で分布が示されます。また、複数の分布を比較する場合、箱ヒゲ図はカテゴリ間の分布を効率的に比較する手段になります。箱ヒゲ図では、ボックス内にデータの真ん中の 50%、つまり 25 ～ 75 パーセンタイルが示され、中央値である 50 パーセンタイルに位置する線が表示されます。

この範囲から外れたデータはどうなるのでしょうか? これが「ヒゲ」の部分です。ボックスの外部にプロットされた垂直線がヒゲで、その上端と下端に水平線が示されます。ヒゲは、データの真ん中の 50% (ボックス) に含まれない値のインサイトを示し、外れ値を区別する境界線が引かれます。外れ値は、頻度の低い非典型の観測値、あるいは分布の中心から極端に外れた値と解釈されます。

箱ヒゲ図の場合、潜在的な外れ値を区別する境界の計算方法が数通り存在します。一部のプログラムでは、極端な外れ値が通常の境界から離れている場合に、その値が別の記号で示されることがあります。

次の例では、建物タイプ別の住宅販売価格の分布を比較しています。一戸建て住宅は、他のどの建物タイプよりも値の範囲がはるかに広く、外れ値と思われる多数の高額住宅の範囲も広がっています。

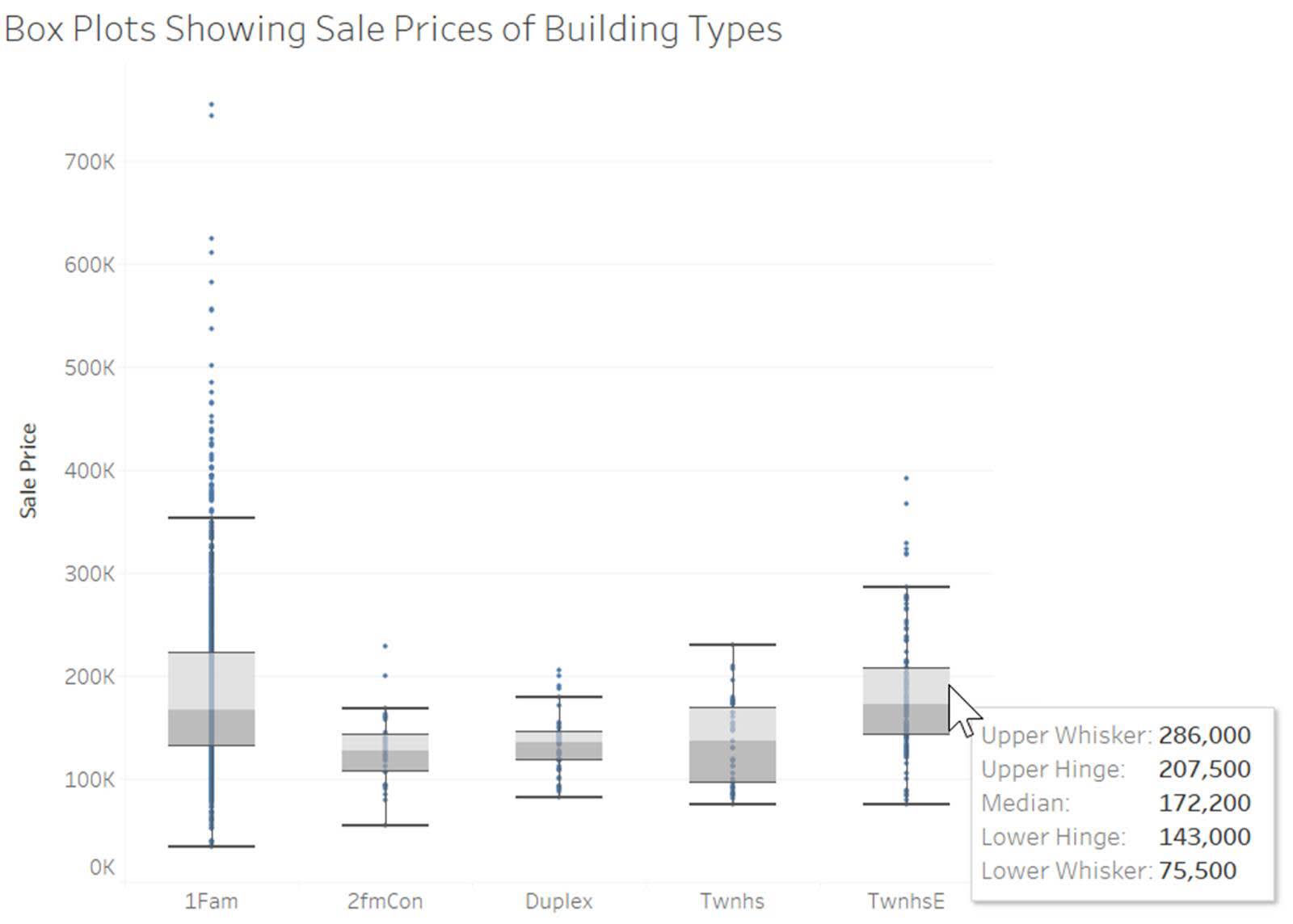
住宅タイプ別の販売価格の分布を比較した箱ヒゲ図

この箱ヒゲ図の例には、個々の値を示す垂直のストリッププロットも示されています。こうすれば、各データポイントと分布の詳細を 1 つのビジュアルで確認できます。箱ヒゲ図の読み取り方を習得するには多少時間がかかるかもしれませんが、箱ヒゲ図は広いスペースを割かなくても、分布に関する多くの情報を伝えることができます。

分布についての詳細は、Trailhead の「データ分布」モジュールを参照してください。

相関

相関の比較では、量的変数間の関係性を検証します。相関は「ある変数の増減に伴って別の変数も増減するか」という質問に答えます。

統計学では、相関という用語に特定の意味を伴う場合があります。たとえば、相関係数について説明する場合は、量的変数間の特定の種類の関係 (通常は線形) を意味します。相関分析と回帰分析の実行方法については、「相関と回帰」モジュールで学習します。

散布図

散布図は 2 つの量的変数の関係を表すために使用され、1 つの変数が x 軸、もう 1 つの変数が y 軸に示されます。散布図では、変数間に関係があるかどうかを示すことができます。たとえば、ある変数が他の変数と「同じ方向」に変化するか、どのような関係 (線形、異なるパターンなど) が存在するかなどがわかります。

散布図を表示すれば、外れ値を見つけることもできます。次の例は、住宅販売価格と居住面積の関係を示しています。散布図の各ポイントは、住宅販売価格を y 軸、面積を x 軸とするグラフに配置された 1 軒の住宅を表します。

住宅販売価格と居住面積の関係を示す散布図

散布図に 2 つの変数の関係が示されることがありますが、一方の変数がもう一方の変数に影響を与えていることを実証するわけではありません。「相関関係は因果関係を実証するものではない」という言葉を聞いたことがあるのではないでしょうか? 変数間の関係はさまざまな理由で生じる可能性があります。

傾向線

散布図の傾向線は、関係の全般的なパターンを見出し、データの全体的な形状を要約する場合に役立ちます。住宅販売価格と面積のこの例では、線形の傾向線から両者の関係の全般的なパターンがわかります。

住宅販売価格と居住面積間の関係を示す散布図と傾向線

すべての関係が線形とは限りません。関係の形状が曲線の場合は、線形の代わりに、指数曲線や対数曲線などの傾向線を使用できます。

相関や、線形回帰線の作成についての詳細は、Trailhead の「相関と回帰」モジュールを参照してください。

サイズの異なるバブルを使用した散布図とテーブルレンズ

上記の散布図では、1 つの変数を x 軸、もう 1 つの変数を y 軸とする 2 つの量的変数の関係を示しました。3 つ以上の量的変数を比較する場合はどうすればよいのでしょうか? もう 1 つの属性であるサイズを使用すれば、散布図に 3 つ目の変数を追加できます。

HealthDataViz の次の例では、一人当たりの GDP とワクチン接種率をそれぞれ x 軸と y 軸に示し、人口数を各バブルのサイズで表しています。

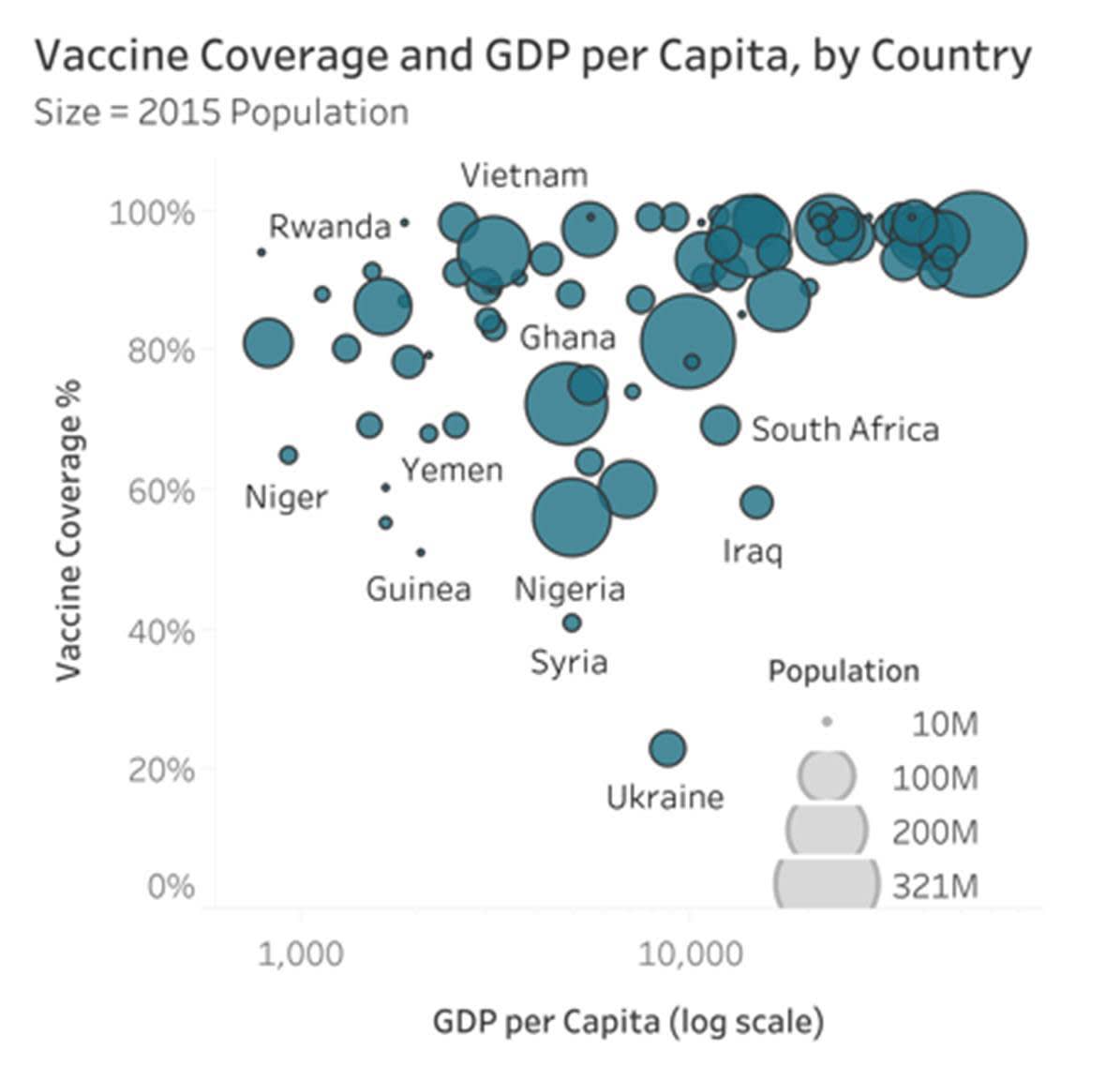
国別のワクチン接種率 (%)、一人当たりの GDP、人口をサイズの異なるバブルで示している散布図

このモジュールの前半で、量的な値をサイズで示した場合、チャートの読み手が長さなど他の属性ほど正確に差異を認識できないことを説明しました。散布図に 3 つ目の量的変数を追加する場合、他にオプションがあまりないため、散布図にサイズの異なるバブルを使用するのが一般に認められている方法です。ただし、3 つ目の変数にサイズの異なるバブルを使用すると、その表示の精度が低下します。

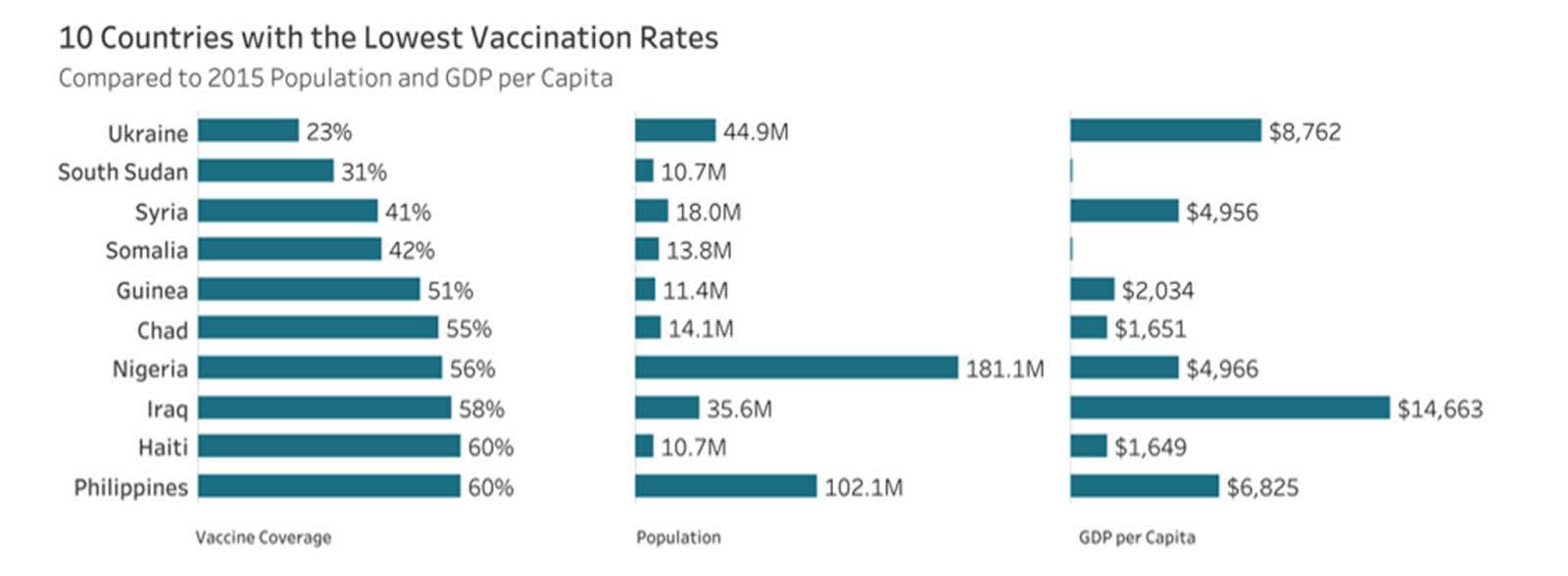
データポイントがさほど多くない場合や、いずれかの変数の上位または下位の値セットのみを比較したい場合は、テーブルレンズに棒グラフを使用するという代替策もあります。テーブルレンズを使用すると、3 つ以上の量的変数を共通の質的 (カテゴリ) 変数で比較できます。

この例では、サイズの異なるバブルを使用した上記の散布図と同じ変数を示していますが、ワクチン接種率の下位 10 か国のみが表示されている点が異なります。テーブルレンズでは、複数のメトリクス間で比較することや、個々のメトリクス内で比較することができます。

国別のワクチン接種率 (%)、一人当たりの GDP、人口を示すテーブルレンズ

予想時間

トピック

ヘルプをお探しですか?

Tableau のリソース