集計

学習の目的 

この単元を完了すると、次のことができるようになります。

• 集計を定義する。
• さまざまな集計種別を適用する。

集計とは?

集計とは、量的データのコレクションを指し、データの大きな傾向を示すことができます。たとえば、特定のキャンプ場に対するすべての Web 検索を合計したり、ある都市における全賃金所得者の収入の平均を出したりすることが可能です。 

多くの分析ツールでは、量的変数はデフォルトで集計されますが、データソースの全行のすべての値についてデータポイントを表示するように集計を解除 (カテゴリ別に分類) することができます。

一般的な集計として、次のようなものがあります。

集計の例

集計の例とデータ分析に与える影響を見てみましょう。オンライン語彙テストに関連する調査データを使用します。各参加者は、オンライン語彙テストを受けた後にデモグラフィックに関する質問に回答しました。 

集計された量的変数を使用したビジュアライゼーションを見る

次のビジュアライゼーションで、量的変数である [Age (年齢)] に注目してください。合計 (Sum) 集計によって [年齢] 変数のすべての値が加算されており、合計が 420,085 歳になっていることがわかります。

上のグラフでは、データセット内のすべてのデータ (12,168 行) が、1 つの数値として 1 つの棒で集計されています。

この Sum of Age (年齢の合計) のビジュアライゼーションは、教育レベルの高さで分類できます。そうすると、各教育レベルの合計年齢を示す棒になります。(各値を加算すると、1 つの棒の合計と同じになります。116,602 + 160,542 + 120,351 + 22,092 + 498 = 420,085)

重要: 116,602 歳という年齢は意味をなさないため、ここでは合計は適切な集計ではありません。この例の年齢のように、変数によっては、合計集計の使用が有用ではない、またはデータ表現として適切ではない場合があります。(別の例では、合計が適切な場合もあります。)ビジュアライゼーションを作成または表示するときに、分析とグラフで使用される集計に注意を払うことが重要です。

参照元データを表示する

どのような値が合計されているのかをより深く理解するために、未加工データを見てみましょう。行レベルのデータを調べると、各参加者の教育レベルと年齢の行があります。 

教育レベルの [Choose not to say (回答拒否)] を見ると、年齢の合計は 498 歳です。

13 + 13 + 13 + 13 + 15 + 16 + 16 + 16 + 17 + 17 + 18 + 20 + 20 + 23 + 37 + 45 + 53 + 65 + 68 = 498 歳

平均集計の影響を見る

先ほどと同じ棒グラフを見てみましょう。ただし、集計を平均 (Average) に変更します。すべての年齢を加算した値を表示する代わりに、棒の高さは平均値を表します。教育レベルごとに、すべての年齢を加算して、値の数で除算されています。

教育レベルの [回答拒否] (水色表示) を見ると、平均は 26.21 歳です。

13 + 13 + 13 + 13 + 15 + 16 + 16 + 16 + 17 + 17 + 18 + 20 + 20 + 23 + 37 + 45 + 53 + 65 + 68 = 498

498 ÷ 19 = 26.21

これで、数値が人にとって現実的な年齢 (20 〜 43 歳) になりました。また、概して、年齢の低い回答者の教育レベルは低くなっています。

中央値集計の影響を見る

[年齢] がデータセットの中央値として集計される場合はどうなるでしょうか? 平均は、極値によって引き伸ばされる、または歪む場合があります。たとえば、103 歳の人が 1 人テストを受けた場合、その教育カテゴリの参加者が全体的に高齢であるように見える可能性があります。極値による歪みの問題を回避するために、中央値 (MEDIAN) 集計では、すべての値が順番 (最大値大から最小値、または最小値から最大値) にランク付けされ、中央値を返します。 

教育レベルの [回答拒否] (水色表示) を見ると、年齢の中央値は 17 歳です。

13、13、13、13、15、16、16、16、17、17、18、20、20、23、37、45、53、65、68 

このグラフから、年齢の中央値は少し低いことがわかります。このテストを受けるのに年齢制限はありませんが、参加条件は 13 歳以上であるため、中央値は低くなることが予想されます。これは、平均を下げる低年齢の極値が存在しないことを意味します。また、依然として全体的な傾向が現れており、参加者の教育レベルが高くなると、年齢も高くなっています。

最小値と最大値の集計の影響を見る

最小値 (Minimum) 集計では選択されたデータの最小値が返され、最大値 (Maximum) 集計では最大値が返されます。 

教育レベルの [回答拒否] (水色表示) を見ると、年齢の最小値は 13 歳です。

13、13、13、13、15、16、16、16、17、17、18、20、20、23、37、45、53、65、68 

教育レベルの [回答拒否] (水色表示) を見ると、年齢の最大値は 68 歳です。

13、13、13、13、15、16、16、16、17、17、18、20、20、23、37、45、53、65、68 

カウント集計の影響を見る

それでは、[年齢] をカウント (Count) として集計するとどうなるかを見てみましょう。カウントでは、選択したカテゴリについてデータの数値の数が返されます。つまり、年齢ではなく、参加者の数に注目します。 

教育レベルの [Choose not to say (回答拒否)] を見ると、カウントは 19、個別カウント (Count Distinct) は 12 です。個別カウントが 12 になるのは、参加者の中に 13 歳が 4 人、16 歳が 2 人、20 歳が 2 人いたためです。個別カウントの集計では一意の値のみがカウントされるため、12、13、20 が 1 回だけカウントされます。

カウントは、教育レベルの回答を拒否した参加者がほとんどいないことを示しています。

集計解除の例

最初に見たグラフはデータを完全に集計したもので、全体の合計という 1 つの数値がありました。その後で、完全なデータセットの集計を解除して教育レベルで分類し、各教育レベルの年齢の合計値の内訳を示しました。データセット内のすべての年齢の合計値 (または平均値や最小値) を見る代わりに、各棒を各教育レベルで集計しました。データは集計されていますが、より詳細になりました。

ここで元のデータについてもう一度考えてみましょう。

各行は参加者を表します。集計値ではなく各参加者の年齢を見たい場合は、データの集計を完全に解除するか、データセットの各ポイントをプロットすることができます。 

データの集計解除の影響を見る

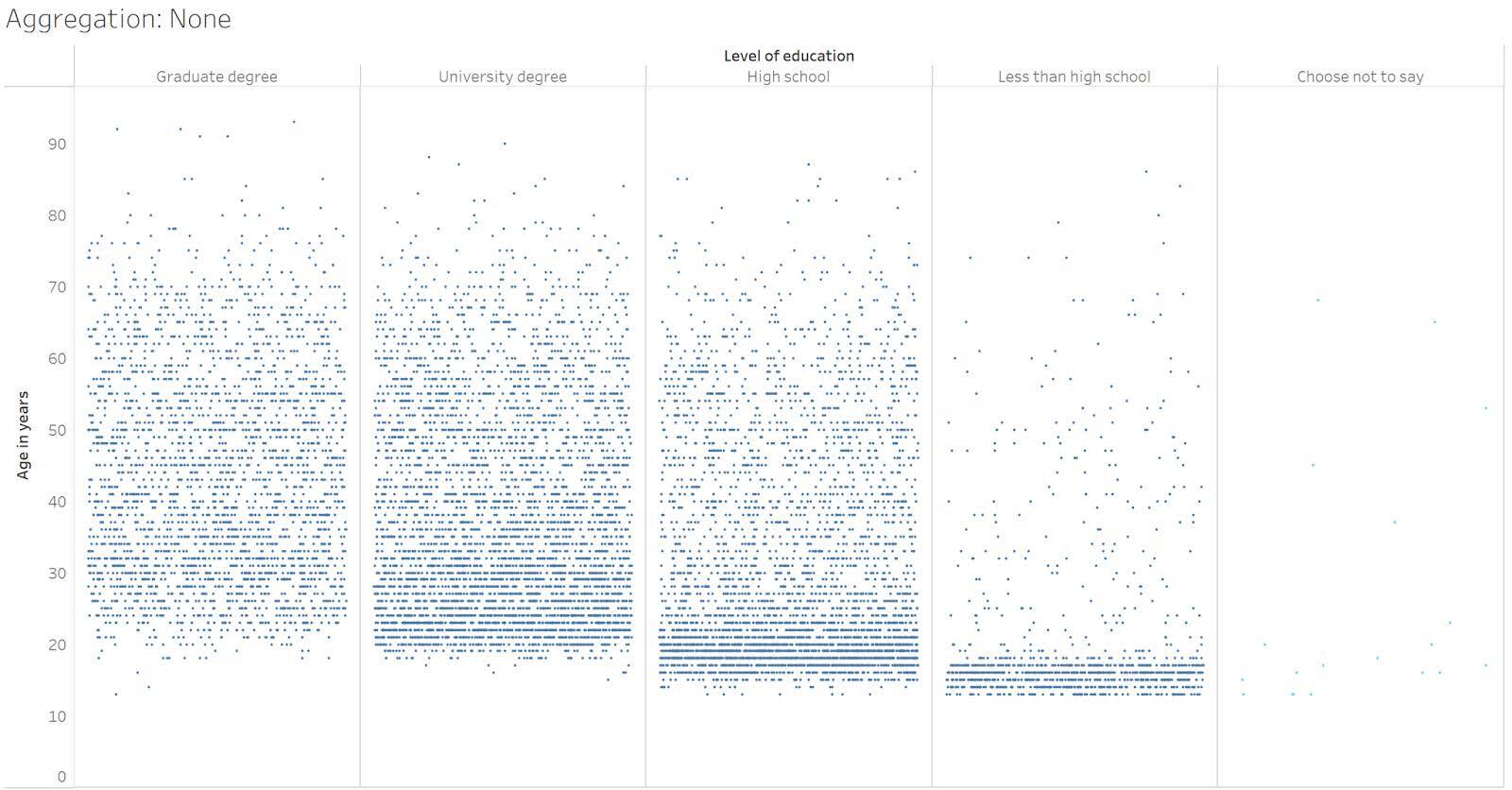
このグラフでは、ジッターを使用してデータポイント (マーク) を分散させています。ジッターとは、データの密度をわかりやすくするために、目盛り間隔のない軸 (ここでは X 軸) に沿ってマークをランダムに配置することを指します。ジッターがなければ、マークはすべて教育レベルごとに 1 つの垂直線上に積み重ねられます。ジッタープロットでは、マークの水平位置はランダムであり、特定の意味はありません。

このビジュアライゼーションでは、参加者の数は年齢の低いほうが多く、年齢が上がるにつれて参加者が少なくなっていることがわかります。また、[Less than high school (中学校以下)] カテゴリには年齢の高い参加者もいますが、大多数は 20 歳未満という若い参加者であることがわかります。[High school (高等学校)] カテゴリは、20 代前半が最も多く、現役大学生であることを示している可能性があります。また、20 歳未満で修士号 (Graduate degree) を持つ参加者はほとんどいません。集計が解除されたデータは、年齢と教育レベルに関する常識に基づいた現実的な期待値とかなりよく一致しています。 

試してみましょう!

課題: 次の表を見てください。1 週間あたりの新聞の読者数に関するデータが 3 行あります。

[1 週間あたりの新聞の読者数] 変数の値 (2、3、7) は、合計値、平均値、中央値、最小値、最大値、カウントとしてどのように集計されますか? 少し考えてから、次の対話型フラッシュカードを使用して答えを確認してください。

各カードの集計種別を読み、その集計がどのような値になるかを考えてください。カードをクリックすると正解が表示されます。右向き矢印をクリックすると次のカードに進み、左向き矢印をクリックすると前のカードに戻ります。 

これで、集計がデータに与える影響とデータの集計を解除した際の結果について学習できました。次の単元では、この概念を踏まえて、粒度について学びます。

リソース 

• Tableau ヘルプ: Tableau でのデータ集計
• Salesforce ヘルプ: 集計関数