Fare confronti basati su deviazione, distribuzione e correlazione

Obiettivi di apprendimento

Al completamento di questa unità, sarai in grado di:

Descrivere i confronti basati sulla deviazione, la distribuzione e la correlazione.
Comprendere le best practice per fare confronti attraverso i grafici.

Deviazione

I confronti basati sulla deviazione si basano sulla misura dello scostamento dei valori rispetto a un valore di riferimento, che può essere un valore medio o un valore soglia.

Grafici a barre divergenti

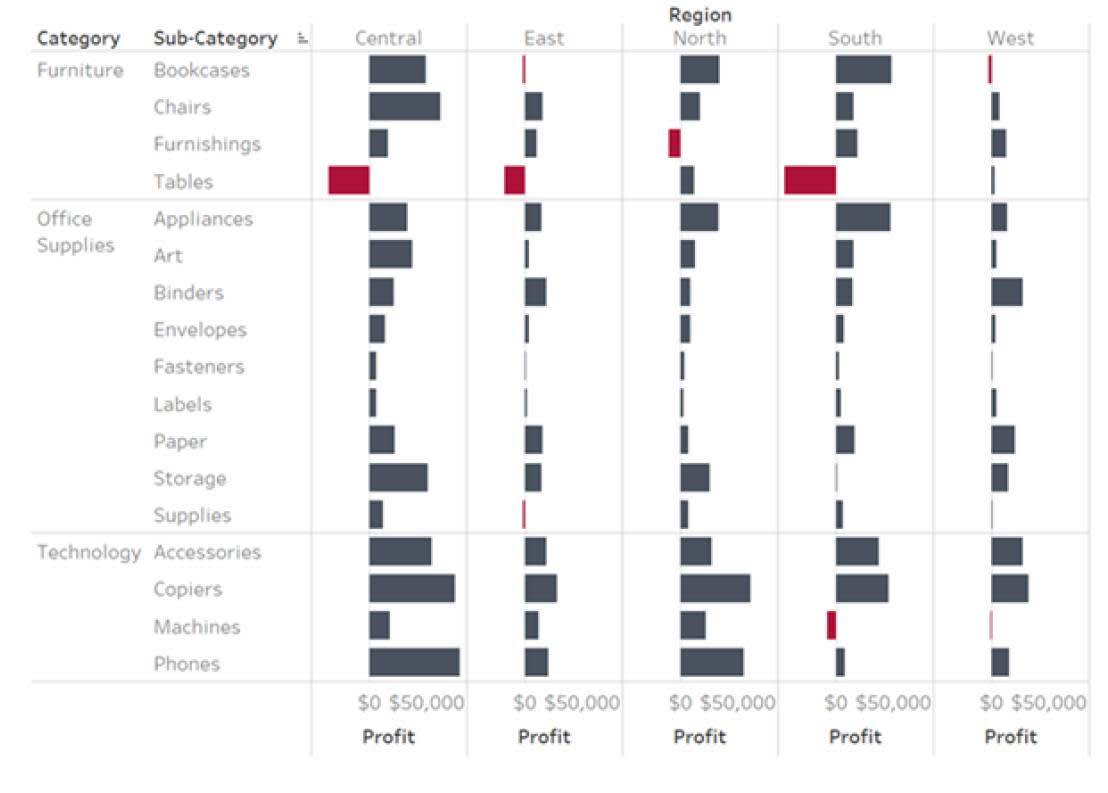
Nell'esempio seguente, la lunghezza delle barre mostra la distanza rispetto a un valore centrale pari a zero per indicare l'ammontare degli utili o delle perdite. Puoi vedere a colpo d'occhio quali elementi e regioni non generano profitti.

Grafico a barre divergenti con utili e perdite per categorie di prodotto e regioni.

Grafici a linee

In precedenza hai appreso che i grafici a linee sono uno dei modi migliori per mostrare variazioni di valori nel tempo. Il grafico a linee è un'ottima opzione anche quando vuoi mostrare una deviazione nel corso del tempo. L'esempio qui di seguito mostra la variazione percentuale nell'arco di un anno del numero di pazienti del Pronto soccorso tra il 2015 e il 2016 per ogni mese. Noterai che il mese di giugno ha registrato la maggiore crescita del numero di pazienti rispetto all'anno precedente.

Grafico a linee che mostra la variazione percentuale nell'arco di un anno tra il 2022 e il 2023 per ogni mese.

Distribuzioni

Una distribuzione mostra tutti i possibili valori dei dati e la frequenza (conteggio) con cui si presentano. In altre parole, una distribuzione descrive quante volte ogni valore è presente in un insieme di dati.

Istogrammi

Ti è mai capitato di usare un'app di mappe sul telefono per scoprire gli orari in cui il tuo ristorante preferito è più affollato? Probabilmente avrai visto il grafico che mostra gli orari di punta. Si tratta di un istogramma. Il picco corrisponde all'orario di punta.

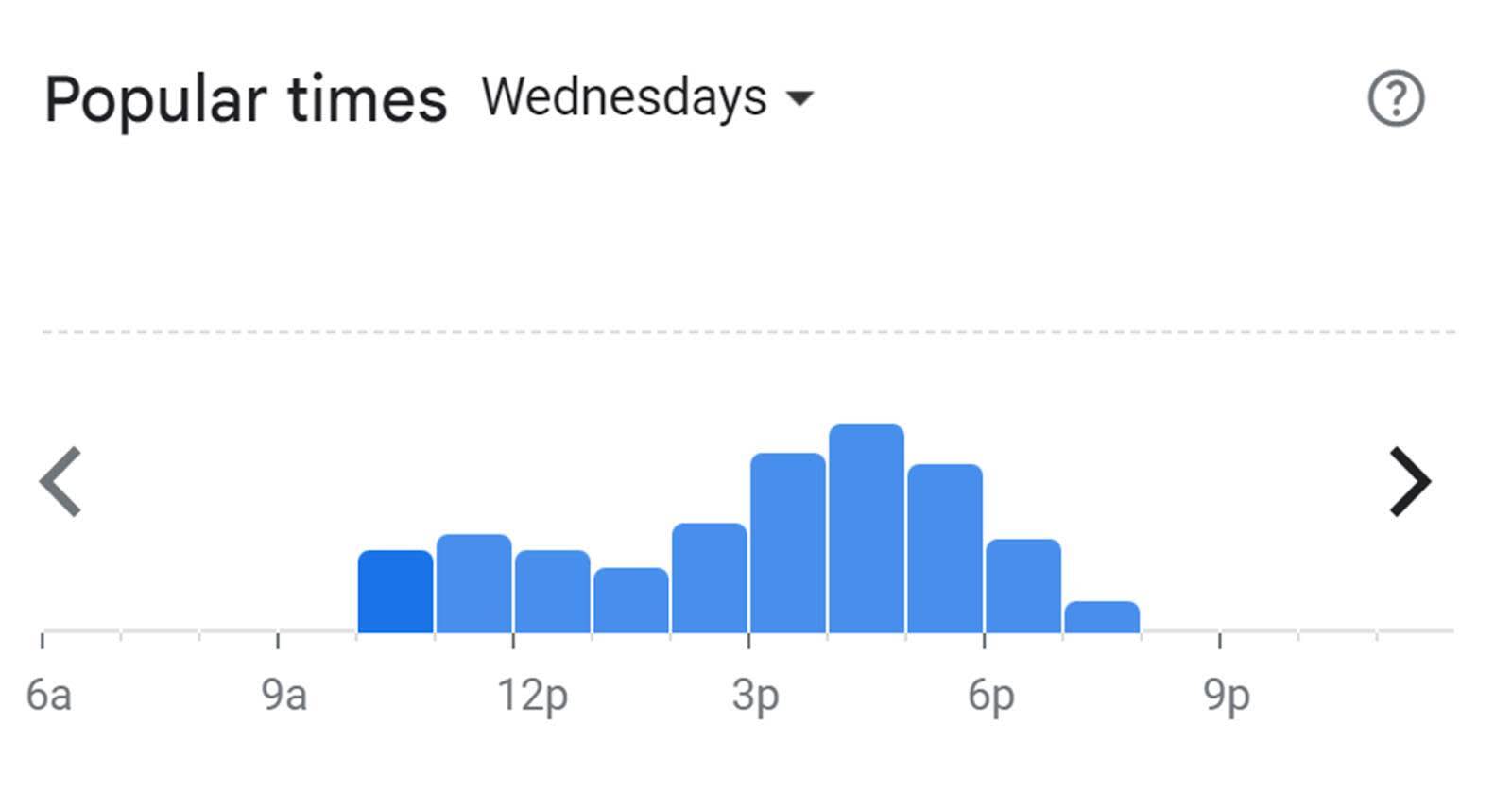
Istogramma di Google Maps che mostra quando un ristorante è più affollato.

Un istogramma è simile a un grafico a barre, ma raggruppa i valori quantitativi in intervalli o contenitori di dimensioni uguali e conta quanti valori sono presenti in ogni contenitore per rappresentarli nella visualizzazione. I programmi come Tableau determinano in automatico la dimensione del contenitore e restituiscono la frequenza (o conteggio) dei valori per ciascun contenitore.

Nell'esempio qui sotto, l'istogramma restituisce una visualizzazione dettagliata dei valori dei prezzi di vendita delle case per l'intero insieme di dati. Nota che il prezzo di vendita della maggior parte delle case si posiziona tra 100.000 e 200.000 dollari. L'istogramma mostra anche che ci sono alcune case che hanno un prezzo superiore rispetto alla maggior parte delle altre.

Istogramma dei prezzi di vendita delle case.

Talvolta le distribuzioni sono presentate come percentuali invece che come conteggi o frequenze.

Poligoni di frequenza

I poligoni di frequenza sono simili agli istogrammi, ad eccezione del fatto che usano le linee per connettere i conteggi relativi alla frequenza. L'esempio seguente illustra gli stessi dati dell'istogramma precedente, ma i conteggi associati a ciascun contenitore sono collegati con una linea e la visione risulta più pulita e semplice.

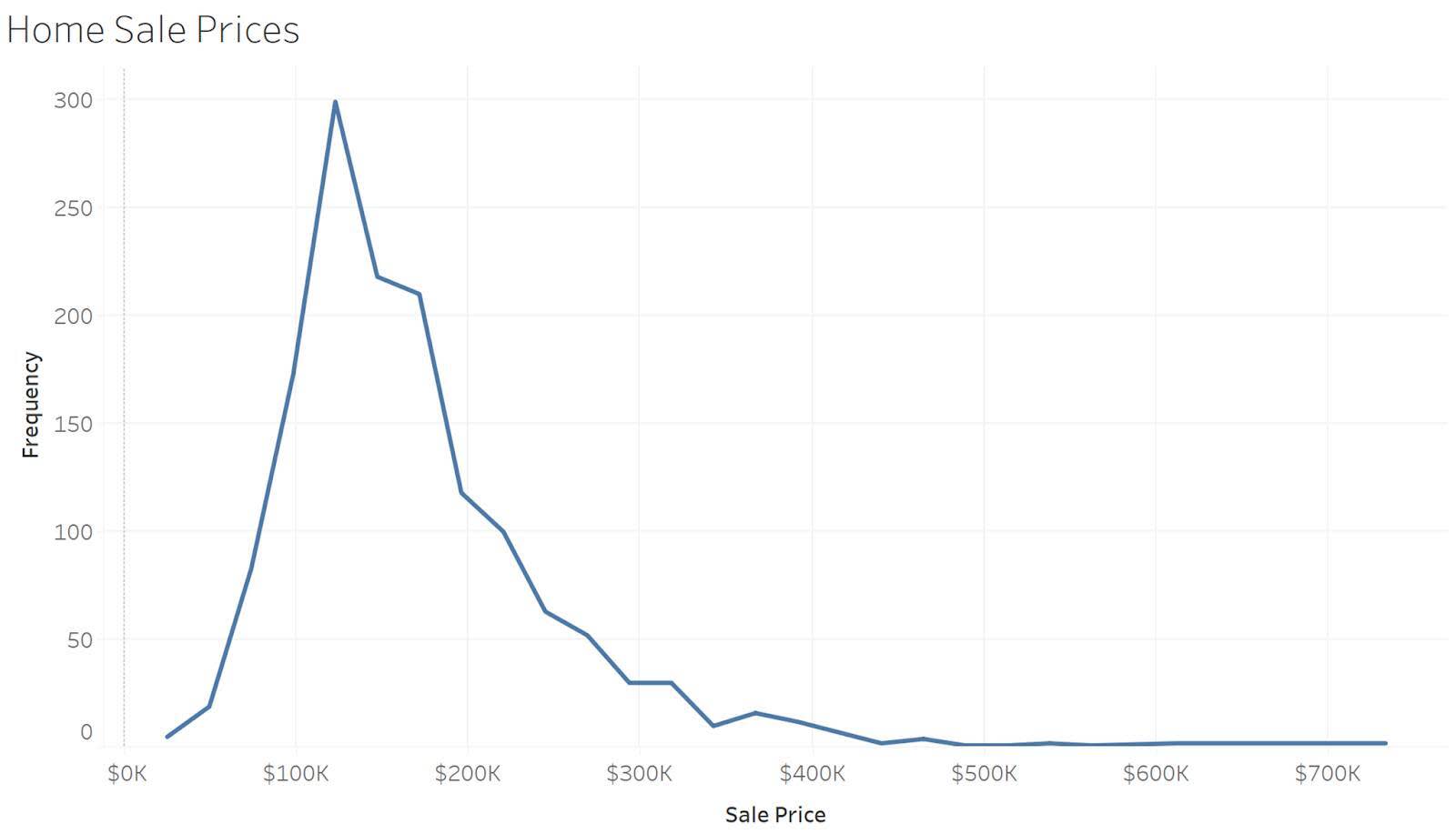
Poligono di frequenza raffigurante la distribuzione dei prezzi di vendita delle case.

Usa i poligoni di frequenza anziché gli istogrammi se vuoi mostrare più di una distribuzione in uno stesso grafico.

Diagramma a punti

I diagrammi a punti, o strip plot, mostrano un punto per ogni valore dei dati su una linea e occupano molto meno spazio rispetto agli istogrammi o ai poligoni di frequenza. I diagrammi a punti possono essere un mezzo efficiente per mostrare l'intervallo di una distribuzione e indicare la presenza di eventuali raggruppamenti di valori in cluster. Se più valori sono uguali o molto vicini tra loro, vengono tracciati l'uno sopra l'altro: questo rende difficile distinguere i valori che ricorrono spesso nei dati.

Nell'esempio seguente, basato sugli stessi dati dell'istogramma, noterai che mentre il diagramma a punti permette di vedere facilmente le rare case con prezzi più elevati, risulta invece difficile visualizzare i prezzi di vendita più frequenti. Pertanto, è consigliabile usare i diagrammi a punti quando si hanno a disposizione insiemi di dati di dimensioni ridotte.

Diagramma a punti che mostra la distribuzione dei prezzi di vendita delle case.

Se si rendono trasparenti i punti di un diagramma a punti, più punti sovrapposti appariranno più scuri e chi guarda il grafico potrà distinguere tra singoli valori e più valori simili.

Diagrammi a scatola

I diagrammi a scatola permettono di mostrare le distribuzioni in una forma più compatta rispetto agli istogrammi. Nel confronto tra più distribuzioni, inoltre, i diagrammi a scatola offrono un modo efficiente per raffrontare le distribuzioni tra categorie. La scatola di un diagramma a scatola rappresenta il 50% dei valori che si situano al centro dell'intervallo di dati, ossia i valori tra il 25° e il 75° percentile, e include una linea che mostra la mediana, o 50° percentile.

E i dati che non rientrano in questi intervalli? È qui che entrano in scena i baffi. Tracciati all'esterno della scatola, i baffi sono linee verticali che finiscono con un tratto orizzontale e forniscono informazioni dettagliate sui valori non compresi nel 50% medio dei dati (la scatola), oltre a indicare un limite per distinguere gli outlier. Gli outlier possono essere intesi come osservazioni atipiche e poco frequenti o come valori che presentano una deviazione estrema dal centro di una distribuzione.

Nei grafici a scatola esistono diversi modi per calcolare il limite in cui dovrebbero trovarsi i potenziali outlier. Probabilmente noterai che alcuni programmi indicano gli outlier estremi con un simbolo diverso se i loro valori sono più lontani dal limite tipico.

Nell'esempio seguente si confrontano le distribuzioni dei prezzi di vendita delle case per i diversi tipi di edifici. Come puoi vedere, le case unifamiliari hanno una gamma di valori molto più ampia rispetto a tutti gli altri tipi di edifici, tra cui diverse case di prezzo più elevato che sembrano essere outlier.

Grafici a scatola che confrontano le distribuzioni del prezzo di vendita di diversi tipi di case.

Questo esempio di grafico a scatola comprende anche diagrammi a punti verticali che mostrano ogni singolo valore. Ora puoi vedere in un'unica immagine tutti i punti dati e i dettagli relativi alla distribuzione. Anche se imparare a leggerli può richiedere del tempo, i grafici a scatola possono offrire molte informazioni su una distribuzione senza occupare troppo spazio.

Per maggiori dettagli sulle distribuzioni, consulta il modulo Distribuzioni di dati su Trailhead.

Correlazioni

I confronti delle correlazioni esplorano le relazioni tra le variabili quantitative. Le domande a cui danno risposta sono, ad esempio: “C'è una variabile che cresce o diminuisce insieme a un'altra variabile?”

In statistica, il termine correlazione può avere significati specifici. Ad esempio, quando si parla di coefficienti di correlazione, si fa riferimento a un tipo ben preciso di relazione tra variabili quantitative, di solito lineare. Nel modulo Correlazione e regressione imparerai a eseguire analisi di correlazione e regressione.

Grafici a dispersione

I grafici a dispersione vengono utilizzati per mostrare la relazione tra due variabili quantitative con una variabile visualizzata sull'asse x e l'altra sull'asse y. I grafici a dispersione possono mostrare se esiste una relazione tra le variabili. Ad esempio, possono mostrare se una variabile “va nella stessa direzione” dell'altra e qual è il tipo di relazione esistente tra le due, ad esempio lineare o che segue un altro schema.

La visualizzazione dei grafici a dispersione può anche aiutarti a individuare gli outlier. L'esempio riportato di seguito mostra la relazione tra il prezzo di vendita delle case e la superficie abitabile. Ogni punto del grafico a dispersione rappresenta una singola casa collocata nel grafico utilizzando il prezzo di vendita della casa sull'asse y e la superficie abitabile sull'asse x.

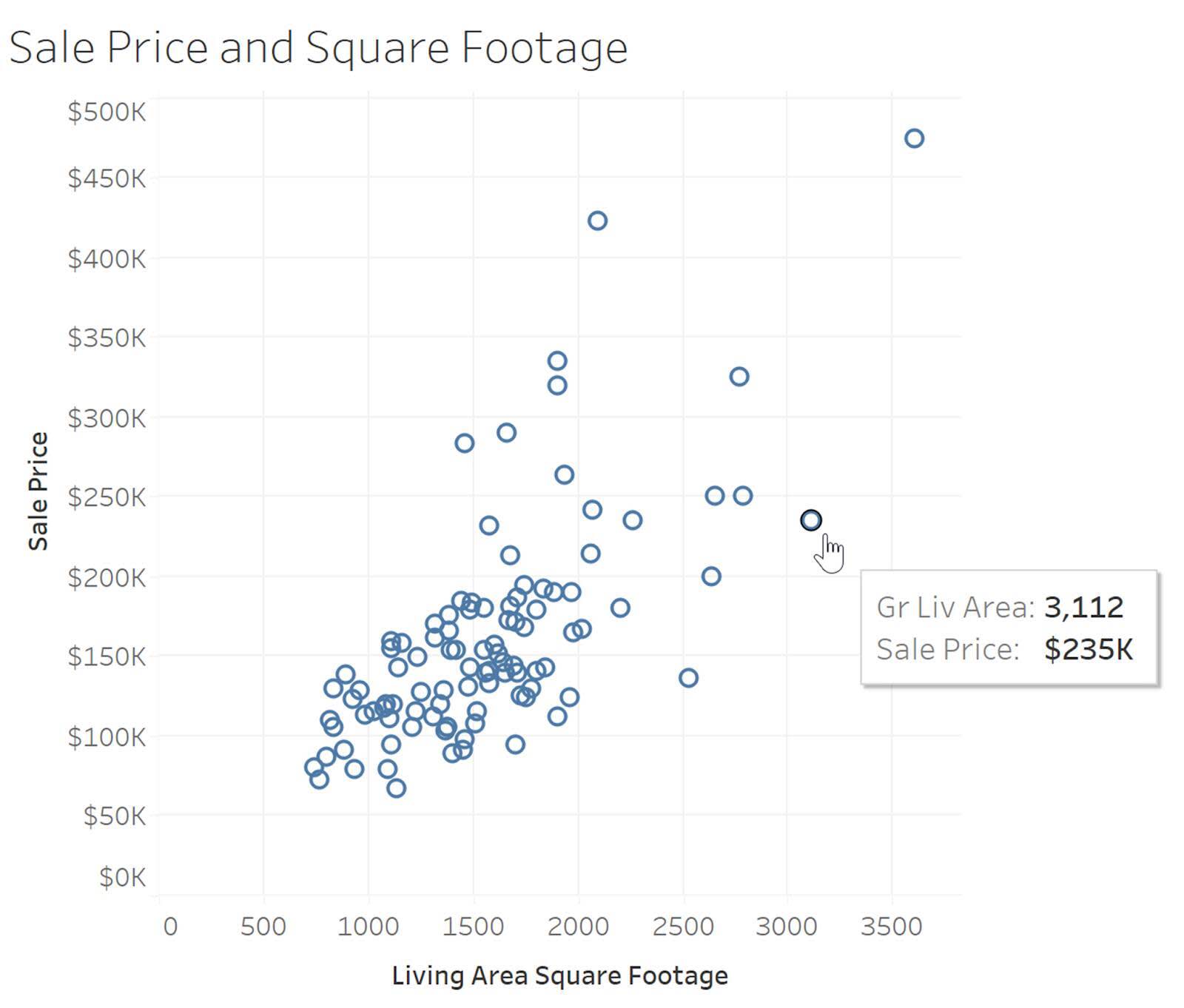
Grafico a dispersione che mostra la relazione tra il prezzo di vendita delle case e la superficie abitabile.

Il grafico a dispersione può mostrare una relazione tra due variabili, ma non dimostra che una variabile influenzi l'altra. Forse conosci il detto “La correlazione non dimostra la causalità”. Le ragioni della relazione tra le variabili possono essere molteplici.

Linee di tendenza

Nei grafici a dispersione, le linee di tendenza ti aiutano a visualizzare lo schema generale della relazione e a riassumere la forma generale dei dati. Nell'esempio del prezzo di vendita delle case e della superficie abitabile, una linea di tendenza lineare permette di visualizzare lo schema generale della relazione.

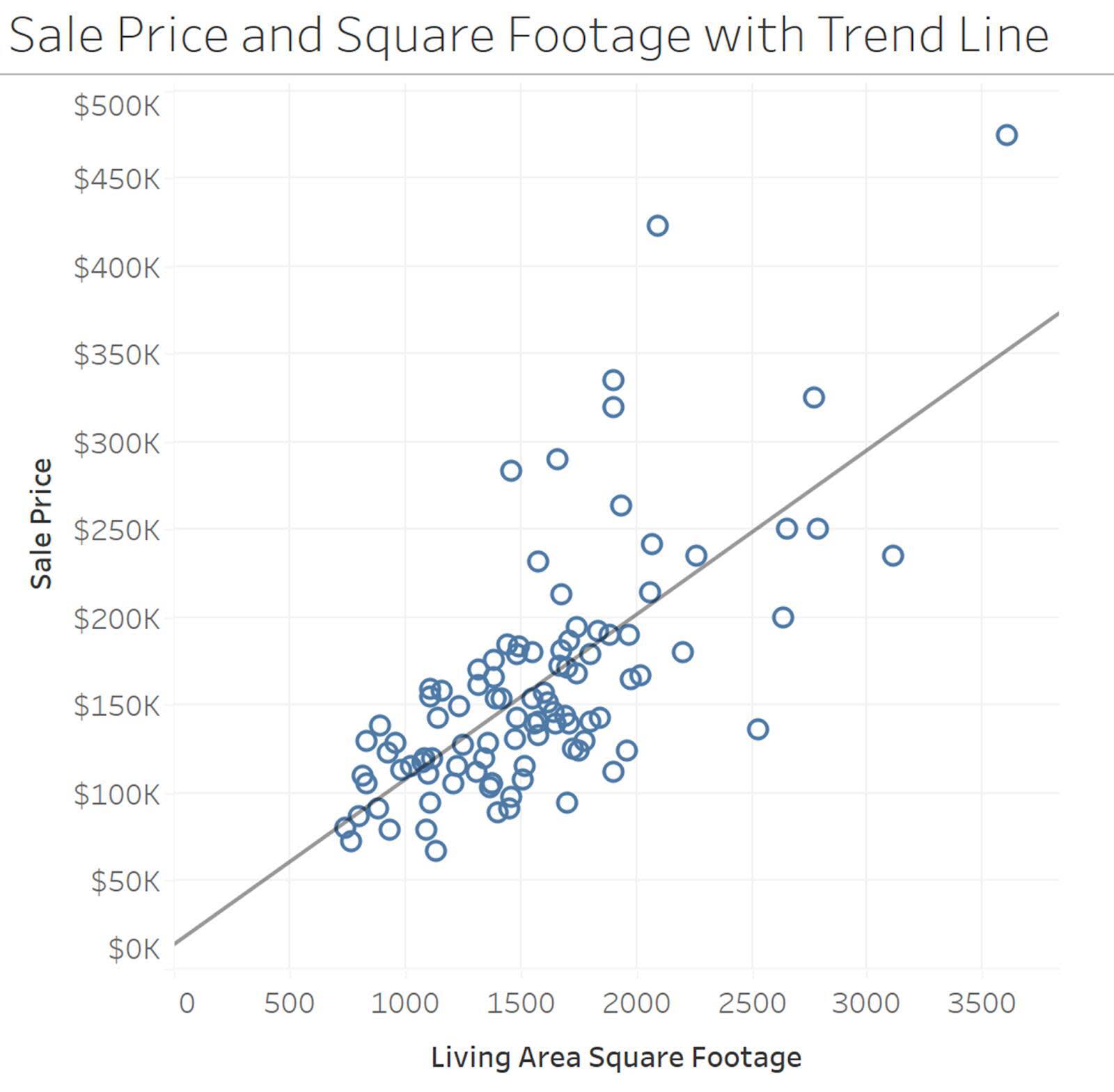
Grafico a dispersione con linea di tendenza che mostra la relazione tra il prezzo di vendita delle case e la superficie abitabile.

Non tutte le relazioni sono lineari. Se la forma della relazione è curva, è possibile utilizzare linee di tendenza esponenziali e logaritmiche anziché lineari.

Consulta il modulo Correlazione e regressione su Trailhead per maggiori dettagli sulla correlazione e sulla creazione di una linea di regressione lineare.

Lente tabella e grafici a dispersione con bolle dimensionate

I grafici a dispersione precedenti mostravano la relazione tra due variabili quantitative visualizzate l'una sull'asse x e l'altra sull'asse y. Ma cosa devi fare se vuoi mettere a confronto più di due variabili quantitative? Per aggiungere una terza variabile a un grafico a dispersione puoi usare un altro attributo: la dimensione.

Nell'esempio successivo, il PIL pro capite e la copertura vaccinale sono mostrati rispettivamente sull'asse x e sull'asse y, mentre la dimensione di ogni bolla rappresenta la dimensione della popolazione.

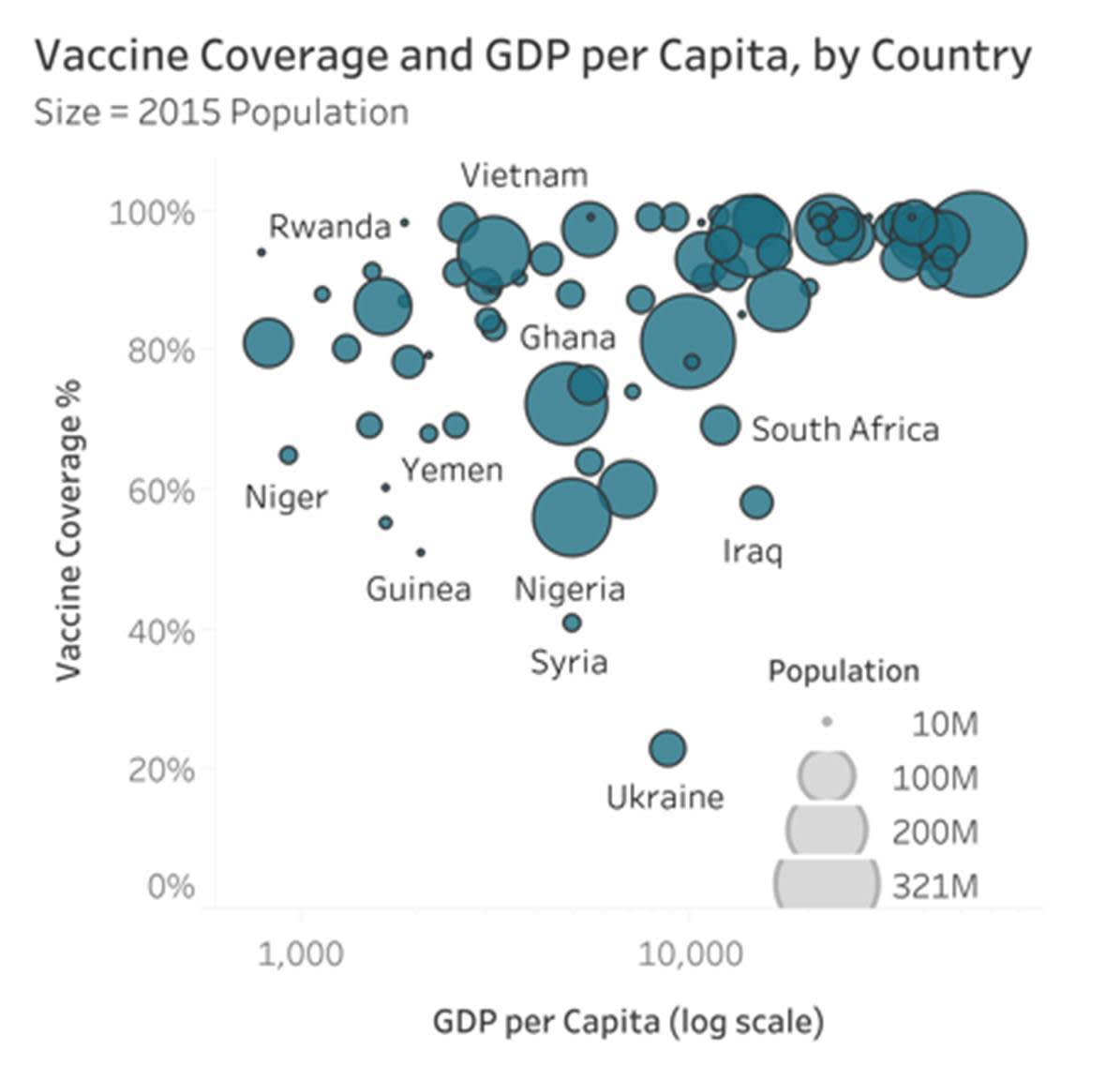
Grafico a dispersione con bolle dimensionate che mostra la copertura vaccinale (%), il PIL pro capite e la popolazione per Paese.

Nel corso di questo modulo hai appreso che i visualizzatori non percepiscono le differenze quantitative delle dimensioni con la stessa precisione di altri attributi, come la lunghezza. Se aggiungi una terza variabile quantitativa a un grafico a dispersione, non hai molte altre opzioni, quindi l'uso di bolle dimensionate nei grafici a dispersione è un metodo accettabile. Quando utilizzi le bolle dimensionate, tieni presente la perdita di precisione della visualizzazione con la terza variabile.

Nelle situazioni in cui non vi sono molti punti dati o vuoi confrontare solo l'insieme di valori più alti o più bassi di una delle variabili, i grafici a barre possono venire in soccorso sotto forma di lente tabella. La lente tabella consente di confrontare tre o più variabili quantitative con una variabile qualitativa (categorica) comune.

L'esempio mostra le stesse variabili del grafico a dispersione con bolle dimensionate mostrato in precedenza, ma presenta solo i dieci Paesi con la copertura vaccinale più bassa. La lente tabella permette anche di effettuare confronti tra più metriche o all'interno di una singola metrica.

Lente tabella che mostra la copertura vaccinale (%), il PIL pro capite e la popolazione per Paese.

Hai bisogno di aiuto?

Scopri di più