Utilisation d’histogrammes pour représenter des distributions de variables continues
Objectifs de formation
Une fois cette unité terminée, vous pourrez :
- Identifier les formes de distribution associées aux variables continues
- Décrire comment utiliser des histogrammes pour représenter la distribution de données
Dans l’unité précédente, vous avez étudié des distributions concernant une variable discrète (la couleur d’un bonbon). Vous avez appris que les variables discrètes comportent des valeurs qui sont indépendantes et distinctes, tandis que les variables continues comportent des valeurs formant un tout ininterrompu. Dans cette unité, vous découvrirez les distributions associées aux variables continues et comment utiliser des histogrammes pour les représenter.
L’exemple suivant est adapté du chapitre sur les distributions de l’ouvrage Online Statistics Education: A Multimedia Course of Study. Chef de projet : David M. Lane, de la Rice University.
Sur une série de 20 tentatives, l’un des auteurs a noté ses temps de réponse dans le cadre du déplacement d’un pointeur au-dessus d’une cible. La variable « Temps de réponse » est continue, et, comme le temps est mesuré en millisecondes, toutes les valeurs sont différentes les unes des autres.
Le graphique présente ces temps de réponse, exprimés en millisecondes.
| Tentative | Temps de réponse, en millisecondes | Tentative | Temps de réponse, en millisecondes |
|---|---|---|---|
|
1. |
568 |
11. |
720 |
|
2. |
577 |
12. |
728 |
|
3. |
581 |
13. |
729 |
|
4. |
640 |
14. |
777 |
|
5. |
641 |
15. |
808 |
|
6. |
645 |
16. |
824 |
|
7. |
657 |
17. |
825 |
|
8. |
673 |
18. |
865 |
|
9. |
696 |
19. |
875 |
|
10. |
703 |
20. |
1007 |
Distributions groupées de fréquence des temps de réponse
Repensez à ce que vous avez appris sur les distributions de fréquence dans l’unité précédente. Si vous présentiez les valeurs de temps de réponse du tableau ci-dessus sous forme de distribution de fréquence, vous auriez 20 valeurs différentes, chacune avec une fréquence de 1. Ce ne serait pas très utile.
Pour résoudre ce problème, vous pouvez créer une distribution groupée de fréquence dans laquelle vous répartissez les temps de réponse en classes (plages de valeurs) d’égale durée, comme dans le tableau.
| Classe (en millisecondes) | Fréquence |
|---|---|
|
500-600 |
3 |
|
600-700 |
6 |
|
700-800 |
5 |
|
800-900 |
5 |
|
900-1000 |
0 |
|
1000-1100 |
1 |
Vous pouvez représenter graphiquement des distributions groupées de fréquence à l’aide d’un histogramme. Les étiquettes sur l’axe des abscisses sont les valeurs intermédiaires des classes qu’elles représentent.
Nous aborderons les histogrammes en détail un peu plus tard. Commençons d’abord par nous intéresser aux différentes formes de distributions et à ce qu’elles peuvent vous apprendre sur les données d’un histogramme.
Formes des distributions
Les distributions se présentent sous différentes formes. Elles peuvent être symétriques, avec les valeurs distribuées autour du centre. Elles peuvent également présenter un biais positif, avec davantage de valeurs se déportant vers la droite, ou un biais négatif, avec davantage de valeurs se déportant vers la gauche.
Imaginez que vous ayez mesuré la taille de personnes de trois groupes différents, et créé un histogramme pour chaque groupe afin de montrer la distribution des tailles des personnes dans chaque groupe.
La taille de classe est de 2,95 pouces, et les tailles sont réparties en classes du type 59-61,95 pouces, 62-64,95 pouces, et ainsi de suite (Tableau Desktop a automatiquement créé la taille de la classe).
Intéressons-nous à la forme de chaque distribution. Dans chacune des distributions présentées ci-dessous, vous remarquerez que les valeurs de la moyenne et de la médiane (la valeur au milieu des points de données) déterminent la forme.
Distributions symétriques
Dans notre exemple, la distribution des tailles pour l’un des groupes est pratiquement symétrique. Si vous repliiez l’histogramme en deux, les deux côtés se chevaucheraient quasiment.
Dans une distribution entièrement symétrique, le milieu des données est représenté à la fois par la moyenne et par la médiane (la valeur au milieu des points de données), car ces valeurs sont égales. Le milieu des données est représenté par les deux valeurs, et la distribution s’étend autant sur la droite que sur la gauche de part et d’autre du centre.
Distributions avec biais positif
Certaines distributions ne sont pas symétriques. Si les données d’une distribution sont davantage distribuées du côté positif que du côté négatif, il s’agit alors d’une distribution avec un biais positif. Une distribution avec biais positif, ou queue droite, présente des données qui sont davantage distribuées sur la droite. La « queue » à droite est donc plus longue. Lorsqu’une distribution est positivement biaisée, la médiane est inférieure à la moyenne.
Imaginons par exemple une ville dont les habitants comptent plusieurs milliardaires. Les revenus très élevés de ces milliardaires auraient pour effet de biaiser le revenu moyen de la ville. Le revenu moyen serait plus élevé que ce qu’il est en réalité. Pour refléter au mieux la situation économique des habitants, il serait mieux adapté de s’appuyer sur le revenu médian.
De même, pour les données sur les tailles, un groupe présente un biais positif en raison de la présence de trois individus mesurant près de 72 pouces (6 pieds) ou plus. Ces tailles élevées font augmenter la moyenne. Ici aussi, il serait plus judicieux de s’intéresser à la médiane pour avoir un aperçu de la taille du groupe.
Distributions avec biais négatif
La distribution avec biais négatif est un autre type de distribution asymétrique. Les données dans une distribution avec biais négatif sont davantage dispersées dans le sens négatif que dans le sens positif. Une distribution avec biais négatif, ou queue gauche, présente des données qui sont davantage distribuées sur la gauche. La « queue » à gauche est donc plus longue. Lorsqu’une distribution est biaisée de manière négative, la médiane est supérieure à la moyenne.
Imaginez par exemple une classe de 20 étudiants. Cette classe compte deux étudiants qui n’ont jamais suivi les cours ni rendu de devoir noté. Ils ont obtenu une note finale de 0,0. Ces deux notes biaiseraient les résultats de la note moyenne obtenue par la classe, ce qui fait que la note moyenne serait inférieure à ce qu’elle est en réalité. Pour refléter au mieux les performances des étudiants de cette classe, il serait plus judicieux de présenter la note médiane obtenue.
De même, pour les données sur les tailles, un groupe présente un biais négatif en raison de la présence d’individus mesurant moins de 60 pouces (5 pieds). Ces tailles plus petites font baisser la moyenne.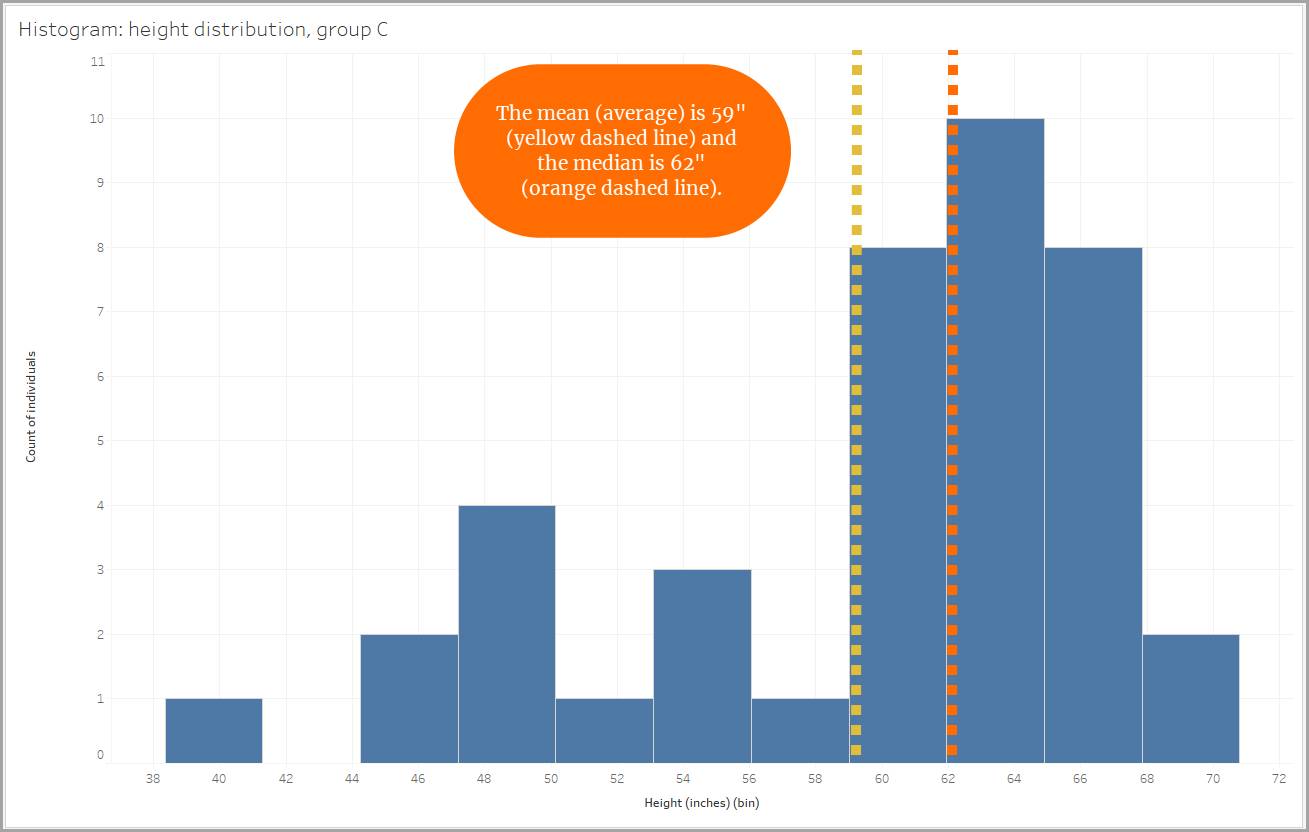
Histogrammes
Tous les graphiques que vous examinez dans cette unité sont des histogrammes. Un histogramme se présente comme un graphique à barres, mais regroupe des valeurs correspondant à une variable continue en plages ou classes de taille égale.
Cet histogramme utilise un ensemble de données contenant des informations au sujet d’athlètes olympiques. L’une des variables contient les âges des athlètes, allant de 18 à 90 ans. Cet histogramme vous permet de voir la répartition des athlètes par tranches d’âge.
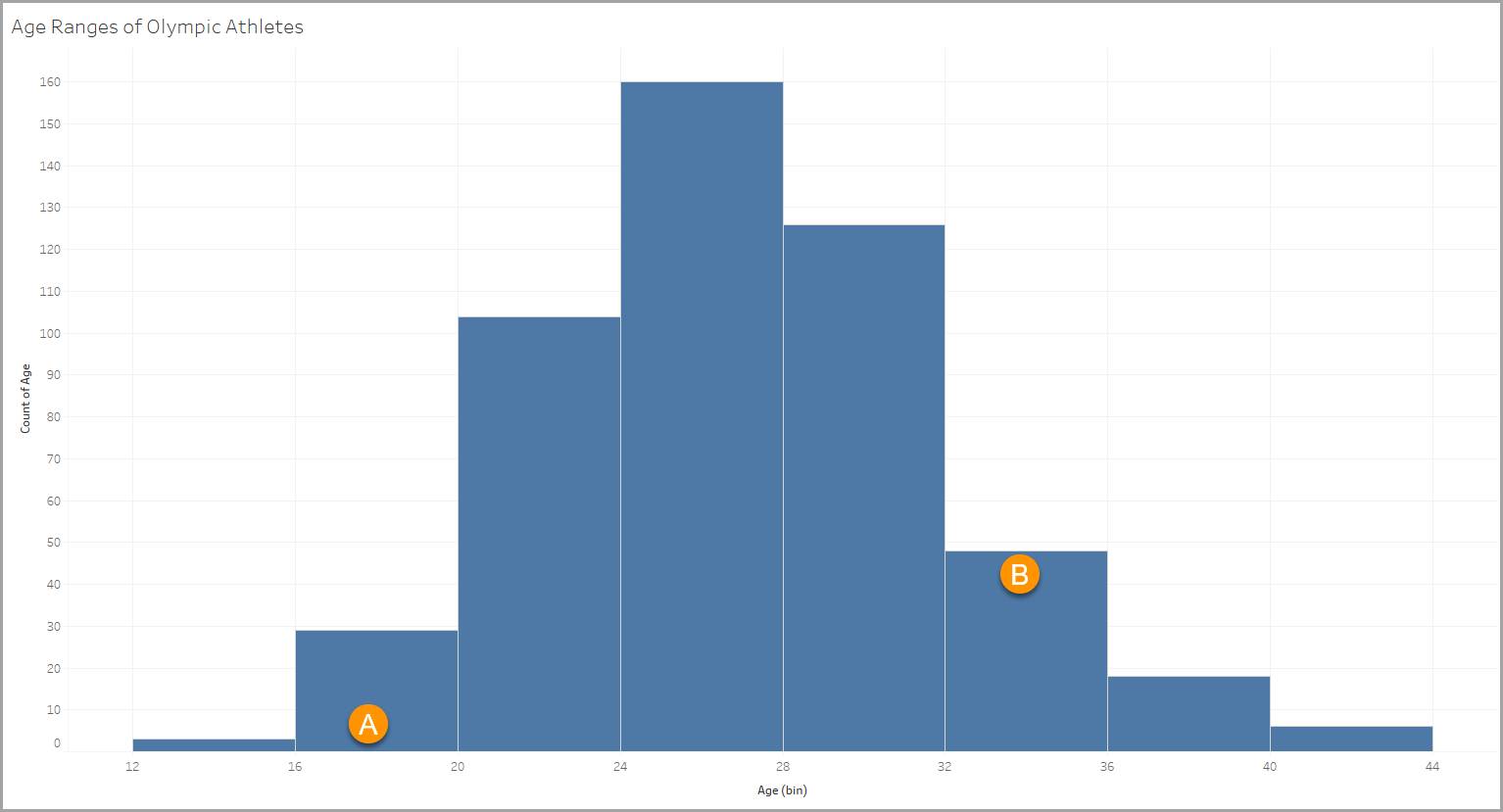
Classes
Chaque classe est définie par une tranche d’âge de quatre années, comme 12-15, 16-19 (A), 20-23, 24-27, etc.
Colonnes
Chaque colonne représente le nombre d’éléments répondant aux critères de la classe (ici, la tranche d’âge). Dans notre exemple, il y a 48 athlètes dans la tranche d’âge 32-35 ans (B).
Vous venez de vous familiariser avec les distributions de variables continues organisées en histogrammes. Dans l’unité suivante, vous découvrirez les distributions de variables continues sous forme de boîtes à moustaches.
