Utilisation de boîtes à moustaches pour représenter des distributions de variables continues
Objectifs de formation
Une fois cette unité terminée, vous pourrez :
- Décrire comment utiliser des boîtes à moustaches pour représenter la distribution des données
- Créer une boîte à moustaches
Vous avez déjà découvert plusieurs manières de représenter les distributions de variables. Cette unité vous présente un autre graphique important, les boîtes à moustaches. Élaborées dans les années 1970 par le mathématicien américain John Tukey, les boîtes à moustaches permettent de présenter des distributions de données et d’exposer des différences en leur sein de manière concise.
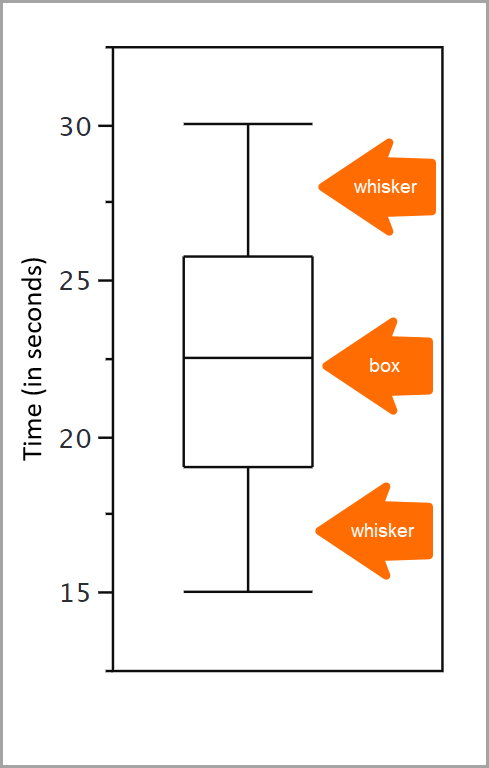
Dans un graphique, une boîte à moustaches représente 50 % des données autour de la médiane. Ces données s’étendent du 25e centile au 75e centile. La médiane est située au 50e centile.
Un centile exprime la manière dont un score se compare à d’autres scores dans un même ensemble de données. Imaginons que vous passiez un test pour mesurer votre degré d’introversion. En lui-même, votre score final est difficile à interpréter. Vous voulez pouvoir le comparer à d’autres scores et connaître le pourcentage de personnes ayant des scores de timidité inférieurs au vôtre. Ce pourcentage est appelé centile. Si 65 % des autres candidats ont été moins timides que vous, votre score correspond au 65e centile.
Pour résumer, la boîte à moustaches d’un graphique affiche les 50 % de données médianes, c’est-à-dire celles allant du 25e centile au 75e centile. Toutefois, qu’en est-il des données qui sont en dehors de ces centiles ? C’est là que les moustaches entrent en jeu : tracées en dehors de la boîte, les moustaches sont des lignes verticales qui se terminent par un trait horizontal. Elles donnent des informations sur les valeurs ne se trouvant pas dans les 50 % médians des données (la boîte), notamment les valeurs aberrantes. Les valeurs aberrantes peuvent être considérées comme étant des observations atypiques et peu fréquentes, ou comme étant des valeurs qui présentent un écart extrême par rapport au centre d’une distribution.
Nous examinerons tous ces concepts plus en détail ultérieurement dans l’unité.
Création d’une boîte à moustaches
L’exemple suivant est adapté du chapitre écrit par David M. Lane sur les boîtes à moustaches dans l’ouvrage appartenant au domaine public intitulé Introduction to Statistics :, A Multimedia Course of Study. Chef de projet : David M. Lane, de la Rice University.
L’auteur a utilisé un test effectué au sein d’une classe de 31 élèves. Chaque élève a reçu une page contenant 30 rectangles colorés, et devait nommer les couleurs le plus rapidement possible.
Les temps que les élèves ont mis, en secondes, pour nommer les couleurs ont été notés dans le tableau suivant.
|
14 |
17 |
18 |
19 |
20 |
21 |
|
15 |
17 |
18 |
19 |
20 |
22 |
|
16 |
17 |
18 |
19 |
20 |
23 |
|
16 |
17 |
18 |
20 |
20 |
24 |
|
17 |
18 |
18 |
20 |
21 |
24 |
| 29 |
Utilisons cet ensemble de données pour créer une boîte à moustaches. Voici une vue d’ensemble des étapes de création à suivre.
- Calculez les centiles.
- Tracez la boîte en fonction des centiles.
- Déterminez la taille d’incrément.
- Ajoutez les moustaches.
- Ajoutez la valeur aberrante.
Calcul des centiles
Rappelez-vous qu’au sein du graphique, les boîtes à moustaches s’étendent du 25e centile au 75e centile des données. Le 50e centile se trouve à l’intérieur de la boîte. La partie inférieure de la boîte (appelée limite du 1er quartile) représente le 25e centile, et la partie supérieure (appelée limite du 3e quartile) représente le 75e centile.
Dans les étapes suivantes, nous allons utiliser une suite de nombres pour voir les centiles.
-
Listez les nombres du plus petit au plus grand.
-
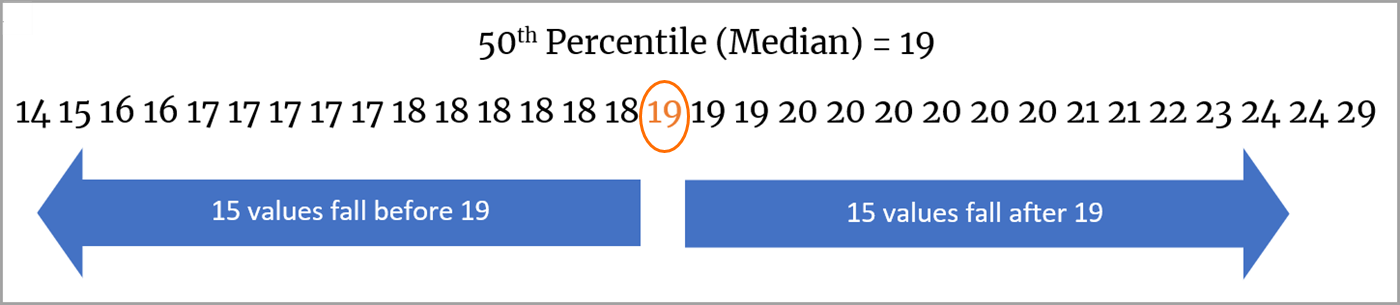
Déterminez la médiane, aussi appelée valeur centrale. La valeur médiane se trouve au milieu de la suite de nombres. Dans le cas de cette suite de 31 nombres, il y a 15 valeurs avant la médiane, et 15 valeurs après celle-ci. Par conséquent, la valeur médiane est 19.
-
Déterminez le 25e centile. La valeur du 25e centile se trouve à mi-chemin entre le début de la suite et la valeur médiane. Dans notre exemple de 31 nombres, il y a 7 valeurs avant le 25e centile et 7 valeurs entre lui et la médiane. Par conséquent, le 25e centile a pour valeur 17.
-
Déterminez le 75e centile. La valeur du 75e centile se trouve à mi-chemin entre la médiane et la fin de la suite de nombres. Dans notre exemple de 31 nombres, il y a 7 valeurs entre la médiane et le 75e centile et 7 valeurs après lui jusqu’à la fin de la suite. Par conséquent, le 75e centile a pour valeur 20.
Traçage de la boîte en fonction des centiles
Traçons la boîte en nous appuyant sur les valeurs que nous avons déterminées.
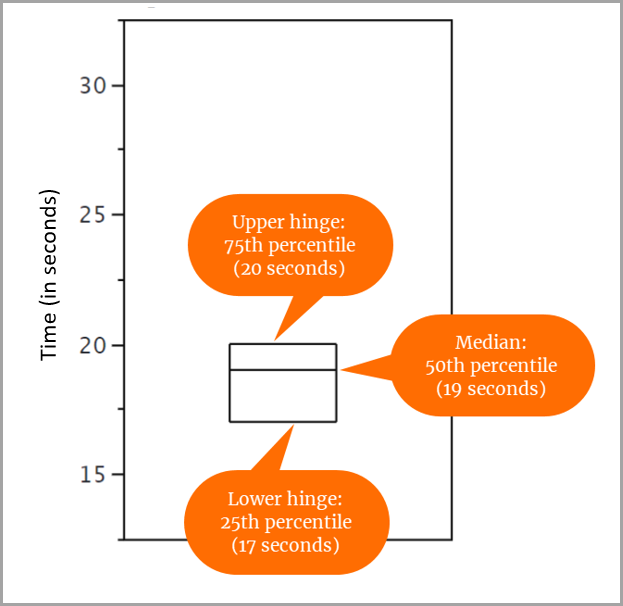
Pour notre ensemble de 31 scores, nous avons déterminé les valeurs suivantes :
- Le 25e centile est 17.
- Le 50e centile (ou médiane) est 19.
- Le 75e centile est 20.
Vous dessinez donc la boîte comme suit.
- Le 25e centile (limite du 1er quartile) est aligné avec la valeur 17 sur l’axe des ordonnées.
- Le 50e centile (médiane) est aligné avec la valeur 19 sur l’axe des ordonnées.
- Le 75e centile (limite du 3e quartile) est aligné avec la valeur 20 sur l’axe des ordonnées.
La boîte représente les 50 % de données qui se trouvent autour de la médiane.
Remarque : les valeurs comprises entre le 25e centile et la médiane sont également appelées 2e quartile, et les valeurs comprises entre le 51e centile (juste après la médiane) et le 75e centile sont appelées 3e quartile. Les valeurs inférieures au 25e centile constituent le 1er quartile, et les valeurs supérieures au 75e centile constituent le 4e quartile. Utilisez des moustaches et d’autres repères pour représenter les valeurs du 1er et du 4e quartile.
Détermination de la taille d’incrément
Vous allez maintenant préparer le tracé des moustaches au-dessus et en dessous de la boîte, pour donner des informations supplémentaires sur la distribution des données. Le placement des moustaches est déterminé par des incréments, où un incrément est égal à 1,5 x EI. L’EI est l’écart interquartile.
Ce terme peut vous sembler complexe, mais en réalité, l’EI désigne simplement la différence entre la valeur du 75e centile et la valeur du 25e centile. Gardez à l’esprit que la boîte est délimitée par les valeurs des 50 % de données autour de la médiane.
Dans notre suite de scores, la valeur du 75e centile est 20 et celle du 25e centile est 17. Ainsi, l’EI est égal à 20 moins 17, soit 3.
Pour déterminer la taille d’incrément, nous multiplions 3 (l’EI) par 1,5, ce qui nous donne 4,5.
Ajout des moustaches
Pour comprendre comment tracer les moustaches, passons d’abord en revue certains termes et la manière dont ils s’appliquent à notre exemple.
Détermination de l’emplacement des moustaches
Vous pouvez tracer des moustaches allant du 25e centile jusqu’à la valeur adjacente inférieure et du 75e centile jusqu’à la valeur adjacente supérieure.
Les moustaches ne vont pas jusqu’aux valeurs aberrantes. Les valeurs aberrantes sont représentées par un petit repère o, et les valeurs éloignées par un astérisque (*).
En ce qui concerne nos données sur les scores, les moustaches s’étendent du 75e centile (20) à la valeur adjacente supérieure (24) et du 25e centile (17) à la valeur adjacente inférieure (14).
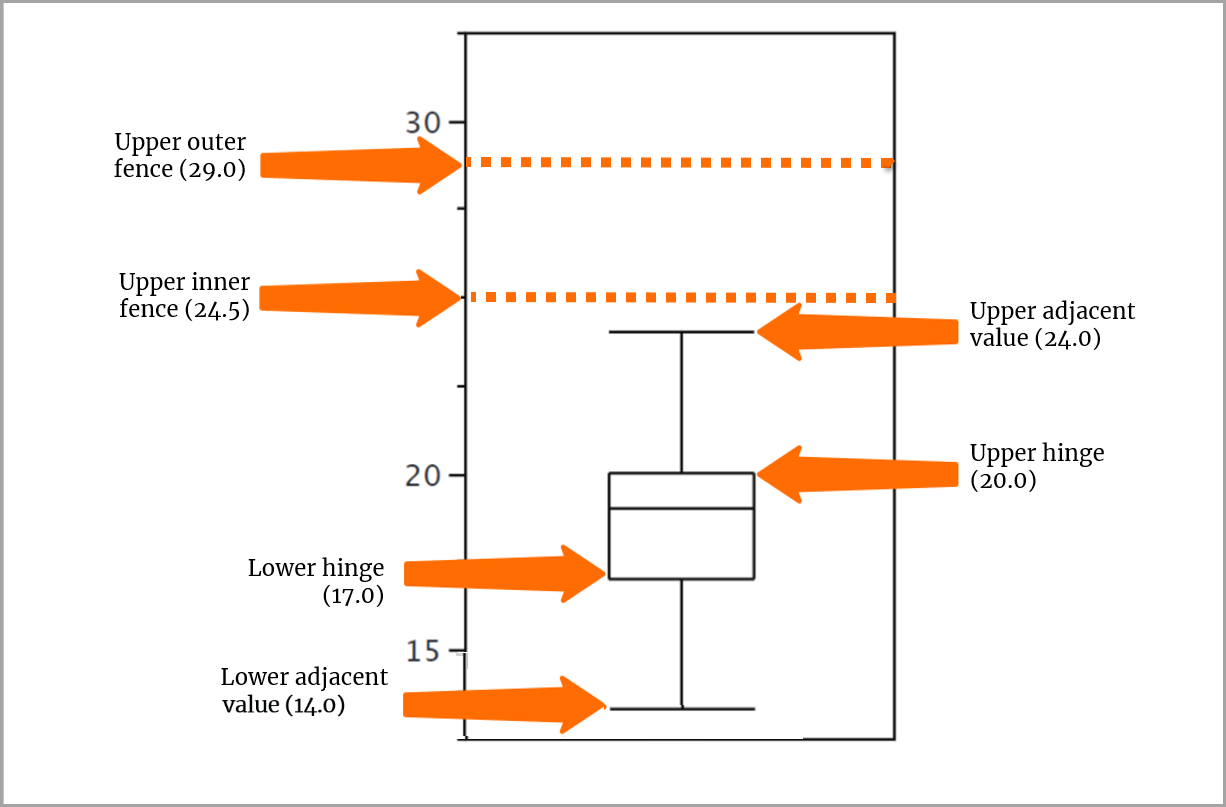
Ajout de la valeur aberrante
Une valeur aberrante est une valeur située au-delà d’une borne intérieure, mais à l’intérieur d’une borne extérieure. Notre ensemble de données en comporte une, 29, qui coïncide avec la valeur de la borne extérieure, mais ne se trouve pas au-delà. Vous utilisez un petit repère o pour représenter cette valeur.
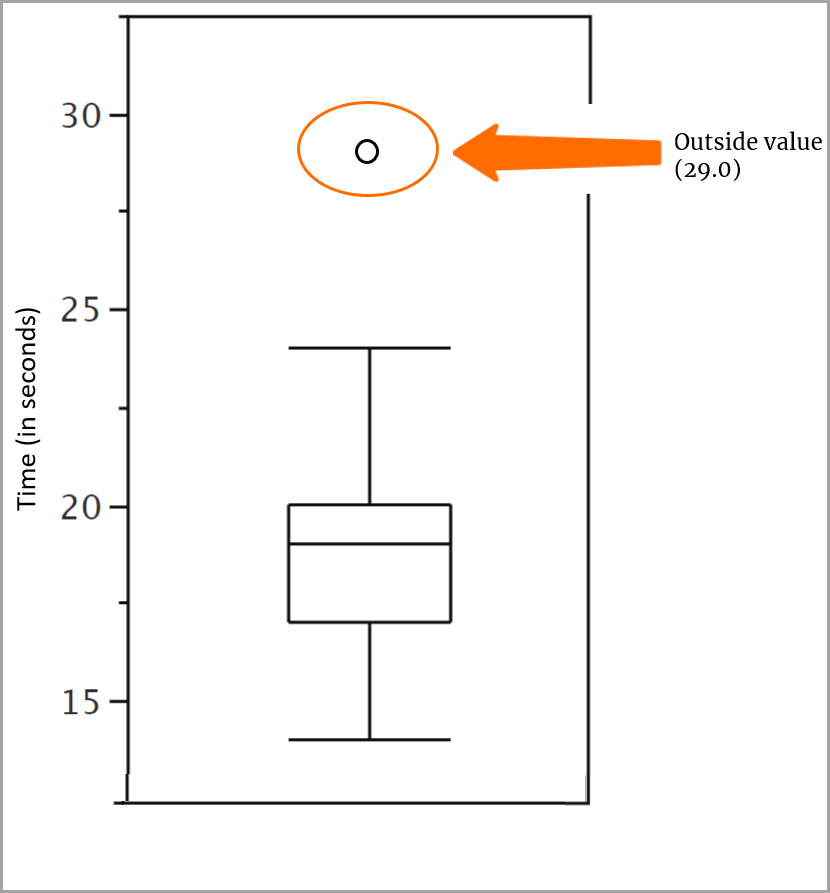
Voilà, votre boîte à moustaches est terminée !
Comparaison entre les boîtes à moustaches et les histogrammes
Vous vous demandez peut-être en quoi les boîtes à moustaches diffèrent des histogrammes pour ce qui est de l’affichage des distributions.
- Les histogrammes utilisent des classes pour représenter la fréquence des valeurs.
- Dans les boîtes à moustaches, l’intérieur de la boîte représente 50 % des données autour de la médiane. Les valeurs aberrantes apparaissent en dehors des moustaches, le cas échéant.
Pour vous donner une idée de ce à quoi cela ressemble, repartons des données montrant les formes des distributions de tailles de personnes. Comparez la façon dont les données apparaissent dans un histogramme et dans une boîte à moustaches.
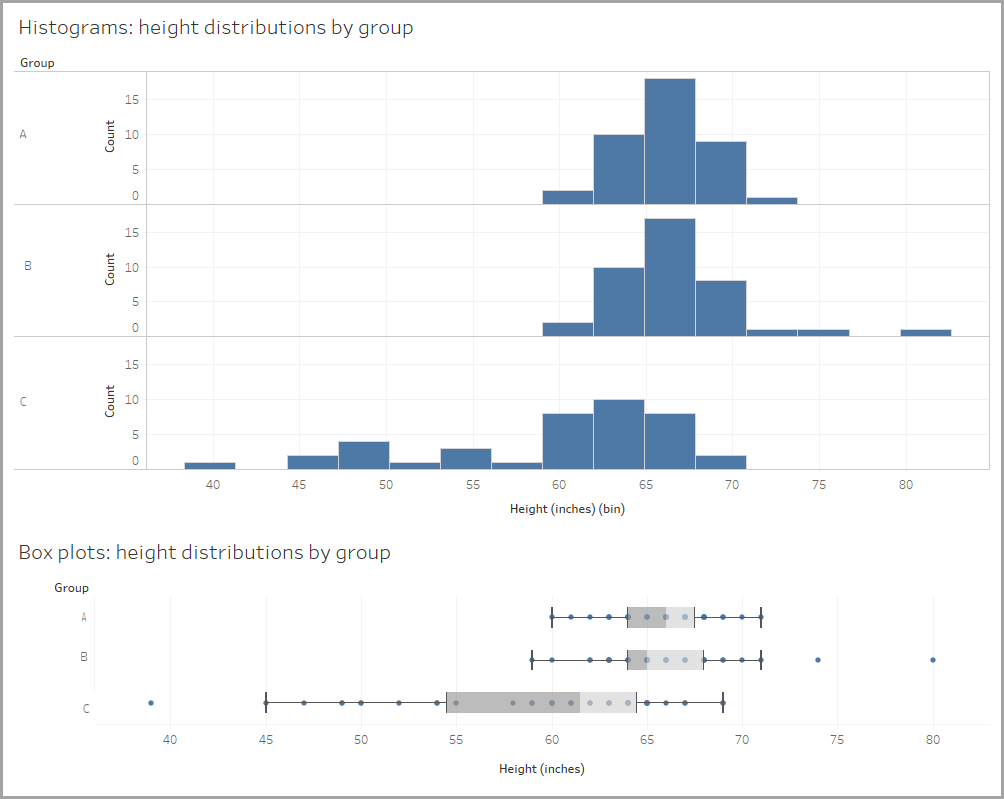
Vous remarquerez qu’une boîte à moustaches prend beaucoup moins de place, ce qui peut permettre de comparer plus facilement les distributions. Il est plus facile de comparer trois distributions côte à côte avec des boîtes à moustaches qu’avec des histogrammes. Voyons quelques autres exemples.
Vous avez découvert dans quelle mesure les distributions peuvent vous aider à explorer des phénomènes, comprendre des situations et communiquer grâce aux données.