Découverte des modes de représentation des distributions de variables discrètes
Objectifs de formation
Une fois cette unité terminée, vous pourrez :
- Définir le concept de distribution de données
- Faire la distinction entre les distributions de fréquence et de proportion pour les variables discrètes
Introduction
Si vous avez terminé le module Des données bien structurées du parcours Développement de vos compétences en data literacy, vous avez appris que les données sont organisées en colonnes (ou champs) et en lignes. Dans des données bien structurées, chaque variable (champ) dispose d’une colonne propre, et chaque observation différente de cette variable (valeur) dispose de sa propre ligne.
Les variables peuvent être discrètes ou continues. Les variables discrètes comportent des valeurs qui sont indépendantes et distinctes, tandis que les variables continues comportent des valeurs formant un tout ininterrompu. Pour en savoir plus sur les variables, consultez le module Types de variables et de champs.
Lorsque vous traitez des données, vous voudrez parfois voir les distributions d’un jeu de données. Une distribution présente toutes les valeurs de données possibles et un nombre représentant leur fréquence d’occurrence. En d’autres termes, une distribution décrit combien de fois chaque valeur de données apparaît. L’organisation d’une distribution varie selon que la variable est discrète ou continue. Intéressons-nous tout d’abord aux variables discrètes.
Distribution de variables discrètes
Lorsque vous observez des distributions de variables discrètes, vous pouvez voir des fréquences (nombre total) ou des proportions (pourcentages). Voici un exemple, adapté de l’ouvrage Online Statistics Education : A Multimedia Course of Study. Chef de projet : David M. Lane, de la Rice University.
Distribution de la fréquence des couleurs de bonbons
Imaginez que vous disposiez d’un sachet de bonbons de six couleurs différentes. Ici, la variable sera la couleur. Comme il s’agit d’une variable qualitative nominale, elle est de nature discrète.
Les variables discrètes peuvent être comptées individuellement. Il vous suffit de vider le sachet et de compter les bonbons. Vous constatez que sur vos 55 bonbons, 17 sont marrons, 18 sont rouges, 7 sont jaunes, 7 sont verts, 2 sont bleus et 4 sont orange.
Ce comptage rapide vous donne la distribution de fréquence des couleurs des bonbons, ou, en d’autres termes, le nombre de bonbons de chaque couleur présents dans le sachet.
Vous pouvez alors créer le tableau de fréquence suivant pour décrire cette distribution.
| Couleur |
Fréquence |
|---|---|
|
Marron |
17 |
|
Rouge |
18 |
|
Jaune |
7 |
|
Vert |
7 |
|
Bleu |
2 |
|
Orange |
4 |
Vous pouvez également utiliser un graphique pour représenter cette distribution de fréquence. Nous avons créé celui-ci à l’aide de Tableau, notre plate-forme d’analyse visuelle.
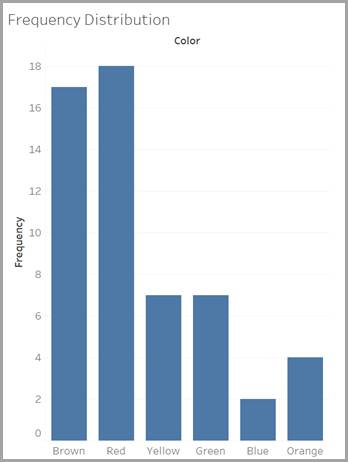
Distribution des proportions des couleurs de bonbons
Notre exemple de distribution de fréquence concernait uniquement votre sachet de bonbons. Toutefois, comment procéder si vous souhaitez connaître la distribution des couleurs dans tous les sachets de ce type de bonbons ?
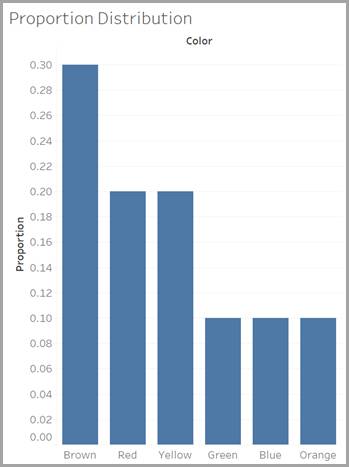
Le producteur fournit quelques informations, mais n’indique pas précisément combien de bonbons de chaque couleur il fabrique. Au lieu de la fréquence (le nombre total de bonbons de chaque couleur produits), la société indique les proportions de chacune des couleurs. Les proportions sont en quelque sorte des pourcentages de chaque couleur produite, exprimés en nombres décimaux. Par exemple, la proportion des bonbons rouges est de 0,20, ce qui signifie que 20 % des bonbons produits sont rouges.
Chaque bonbon étant de l’une des six couleurs, si vous additionnez toutes les proportions, vous obtenez la valeur 1 (ou 100 %).
Le graphique qui présente ces proportions est appelé une distribution des proportions. Le graphique à barres suivant présente la distribution des proportions des couleurs de bonbons, ou, en d’autres termes, le pourcentage que représente chaque couleur dans le total des bonbons produits.
Fiches interactives pour tester vos connaissances
Prêt à tester vos connaissances sur les distributions des fréquences et des proportions ? Examinez ces deux graphiques de distribution concernant une entreprise qui vend trois types de produits : du mobilier, des fournitures de bureau et des outils technologiques. La première fiche indique quel pourcentage du nombre total de commandes représente chacune des trois catégories de produits. La deuxième fiche indique le nombre total de commandes pour chaque catégorie.
Étudiez ces graphiques. Quel est le graphique correspondant à une distribution de fréquence, et quel est celui correspondant à une distribution des proportions ? Cliquez sur la flèche vers la droite pour passer à la fiche suivante et sur la flèche vers la gauche pour revenir à la précédente. Cliquez sur les fiches pour révéler les bonnes réponses.
Vous venez de découvrir deux types de distribution de variables discrètes, l’une correspondant à la fréquence et l’autre aux proportions. Dans l’unité suivante, vous allez apprendre comment représenter la distribution de valeurs continues.
