Réalisation de comparaisons d’écart, de distribution et de corrélation

Objectifs de formation

Une fois cette unité terminée, vous pourrez :

• Décrire les comparaisons d’écart, de distribution et de corrélation
  
• Comprendre les meilleures pratiques pour effectuer des comparaisons à l’aide de graphiques
  

Écart

Les comparaisons d’écart se concentrent sur l’importance de la différence entre les valeurs et une valeur de référence, parfois une moyenne ou un seuil.

Graphiques à barres divergentes

Dans l’exemple, la longueur des barres indique la distance par rapport à une valeur centrale de zéro pour montrer l’ampleur du bénéfice ou de la perte. Ce graphique permet de rapidement repérer les articles et les régions qui ne sont pas rentables.

Graphiques en courbes

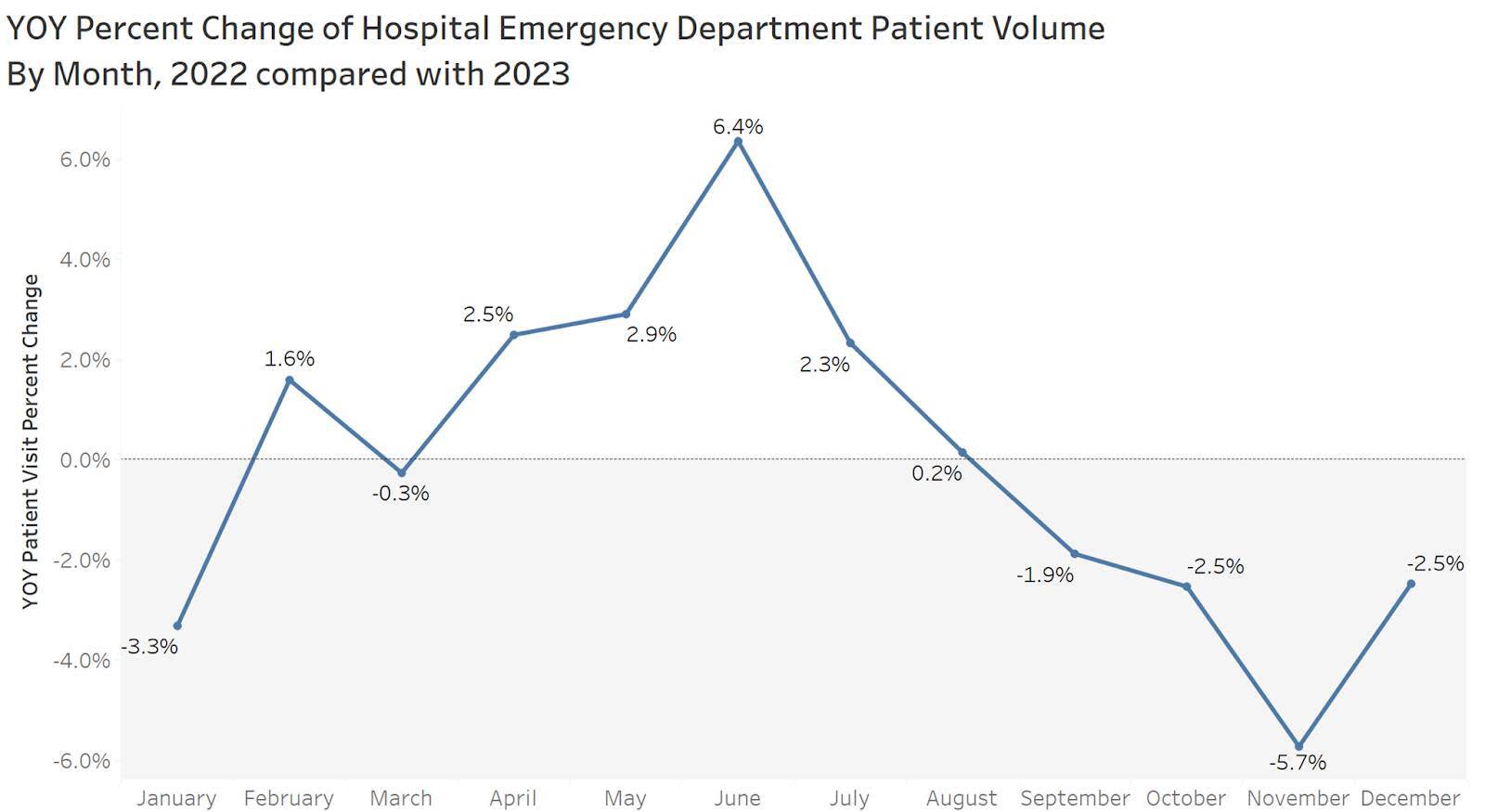
Précédemment, vous avez appris que les graphiques en courbes sont l’un des meilleurs moyens de montrer les changements de valeurs dans le temps. De même, lorsque vous souhaitez montrer l’écart dans le temps, un graphique en courbes est une bonne option. L’exemple suivant présente la variation en pourcentage du volume de patients aux urgences chaque mois d’une année sur l’autre entre 2015 et 2016. Vous pouvez constater que le mois de juin a connu la plus forte augmentation du nombre de patients par rapport à l’année précédente.

Distributions

Une distribution présente toutes les valeurs de données possibles et un nombre représentant leur fréquence d’occurrence. En d’autres termes, une distribution décrit combien de fois chaque valeur apparaît dans un jeu de données.

Histogrammes

Avez-vous déjà utilisé une application de cartographie sur votre téléphone pour connaître les heures d’affluence dans votre restaurant préféré ? Vous avez peut-être remarqué le graphique présentant les périodes d’affluence. Il s’agit d’un histogramme. Le pic indique le moment le plus animé.

Un histogramme est semblable à un graphique à barres, mais il regroupe les valeurs quantitatives en plages de taille égale, ou cellules, et compte le nombre de valeurs dans chaque cellule pour présenter l’histogramme. Lorsque vous utilisez des programmes tels que Tableau, ces derniers déterminent automatiquement la taille des cellules et donnent la fréquence (ou le nombre) de valeurs dans chaque cellule.

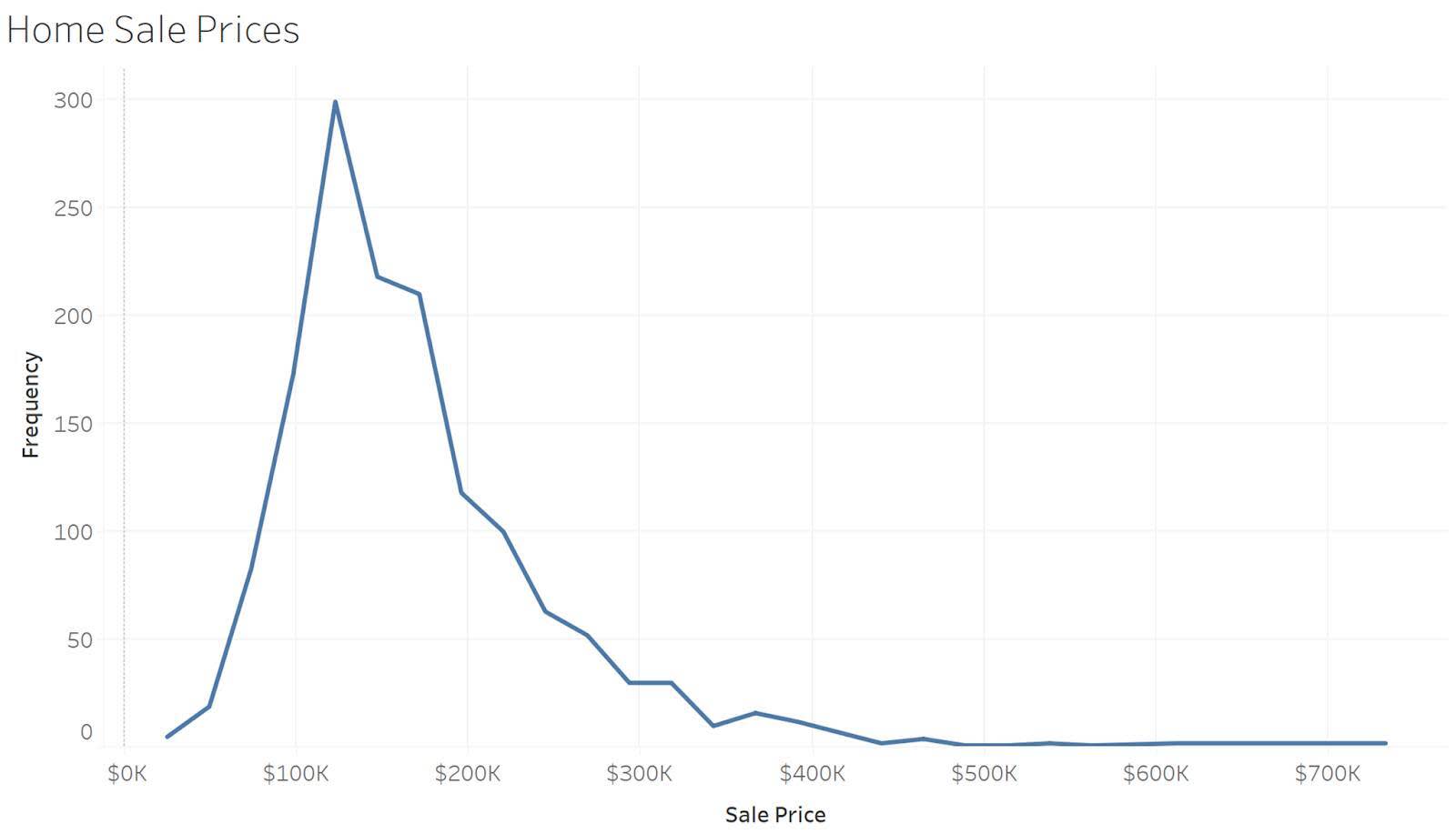
Dans l’exemple suivant, l’histogramme fournit une vue détaillée des prix de vente des logements pour l’ensemble du jeu de données. Vous pouvez constater que la plupart des logements se vendent entre 100 000 et 200 000 dollars. L’histogramme montre également que quelques logements ont un prix plus élevé que la majorité.

Les distributions peuvent parfois être présentées sous forme de pourcentages au lieu de décomptes ou de fréquences.

Polygones de fréquences

Les polygones de fréquences sont semblables aux histogrammes, sauf qu’ils emploient des lignes pour relier les décomptes de fréquence. L’exemple suivant montre les mêmes données que l’histogramme ci-dessus, mais les décomptes de chaque cellule sont reliés par une ligne. La ligne permet de clarifier et de simplifier la lecture.

Choisissez les polygones de fréquences plutôt que les histogrammes lorsque vous souhaitez représenter plus d’une distribution sur le même graphique.

Nuage de points sur un seul axe

Les nuages de points sur un seul axe affichent un point pour chaque donnée sur une ligne et occupent ainsi beaucoup moins d’espace que les histogrammes ou les polygones de fréquences. Les nuages de points sur un seul axe peuvent être un moyen efficace de montrer la plage d’une distribution et un éventuel regroupement de valeurs. Si plusieurs valeurs sont identiques ou très proches les unes des autres, elles sont tracées les unes au-dessus des autres. Il est donc difficile d’y distinguer les valeurs qui reviennent fréquemment dans les données.

Dans l’exemple suivant, qui présente les mêmes données que l’histogramme, vous pouvez voir que si le nuage de points sur un seul axe permet de distinguer facilement les logements individuels à prix élevé, il est difficile d’y voir les prix de vente les plus fréquents. C’est pourquoi les nuages de points sur un seul axe sont adaptés aux jeux de données de taille restreinte.

En rendant les points transparents sur un nuage de points sur un seul axe, il est possible de faire apparaître plusieurs points plus foncés. Ainsi, le lecteur peut faire la distinction entre des valeurs uniques et plusieurs valeurs similaires.

Boîtes à moustaches

Les boîtes à moustaches présentent les distributions sous une forme plus compacte qu’un histogramme. Pour étudier plusieurs distributions, les boîtes à moustaches constituent un moyen efficace de comparer les distributions entre les catégories. Dans les boîtes à moustaches, la boîte représente la moitié centrale des données, ou la plage du 25e au 75e centile, et la ligne représente la valeur médiane, ou le 50e centile.

Toutefois, qu’en est-il des données qui sont en dehors de ces centiles ? C’est là que les moustaches entrent en jeu : tracées en dehors de la boîte, les moustaches sont des lignes verticales qui se terminent par un trait horizontal. Elles donnent des informations sur les valeurs ne se trouvant pas dans les 50 % médians des données (la boîte) et fournissent une limite pour distinguer les valeurs aberrantes. Les valeurs aberrantes peuvent être considérées comme étant des observations atypiques et peu fréquentes, ou comme étant des valeurs qui présentent un écart extrême par rapport au centre d’une distribution.

Avec les boîtes à moustaches, il existe différentes façons de calculer la limite relative aux valeurs aberrantes potentielles. Certains programmes indiquent les valeurs aberrantes extrêmes à l’aide d’un symbole différent si ces valeurs sont plus éloignées que la limite habituelle.

L’exemple suivant compare la distribution des prix de vente des logements selon le type de bâtiment. Vous pouvez constater que les maisons de type pavillon présentent une plage de valeurs beaucoup plus large que les autres types de bâtiments, et cette catégorie comprend de nombreuses maisons plus chères qui semblent être des valeurs aberrantes.

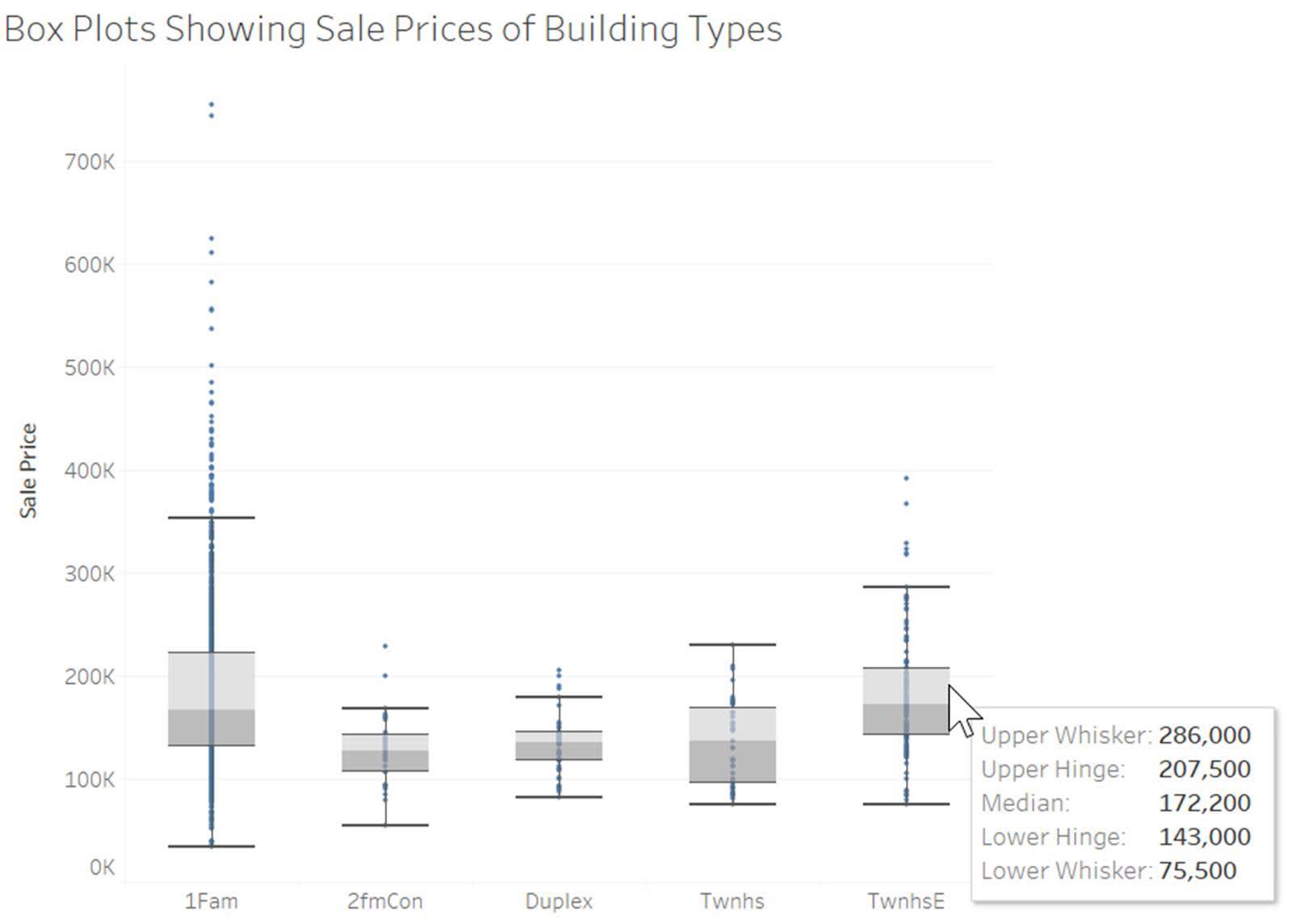
Cet exemple de boîtes à moustaches comprend également des nuages de points sur un axe vertical représentant chaque valeur individuelle. Vous pouvez ainsi visualiser chaque point de données et les détails de la distribution sur la même représentation visuelle. Bien qu’il faille un peu de temps pour apprendre à bien lire les boîtes à moustaches, elles peuvent transmettre beaucoup d’informations sur une distribution sans utiliser beaucoup d’espace.

Consultez le module Distributions des données sur Trailhead pour en savoir plus sur les distributions.

Corrélations

Les comparaisons corrélatives explorent les relations entre variables quantitatives. Elles répondent à des questions telles que : « Une variable donnée augmente-t-elle ou diminue-t-elle en même temps qu’une autre variable ? »

En statistiques, le terme « corrélation » peut avoir des significations spécifiques. Par exemple, lorsque l’on parle de coefficients de corrélation, il s’agit d’un type spécifique de relation entre variables quantitatives, généralement linéaire. Dans le module Corrélation et régression, vous apprenez à effectuer des analyses de corrélation et de régression.

Nuages de points

Les nuages de points permettent de montrer la relation entre deux variables quantitatives, une variable étant représentée sur l’axe x et l’autre sur l’axe y. Les nuages de points peuvent montrer s’il existe une relation entre les variables. Par exemple, une variable « va-t-elle dans la même direction » que l’autre, et la relation est-elle linéaire ou d’un autre type ?

La visualisation des nuages de points peut également vous aider à repérer les valeurs aberrantes. L’exemple suivant illustre la relation entre le prix de vente d’un logement et la surface habitable. Chaque point du nuage de points représente un seul logement dans le graphique en indiquant le prix de vente du logement sur l’axe y et sa superficie sur l’axe x.

Bien qu’un nuage de points puisse montrer une relation entre deux variables, il ne prouve pas qu’une variable affecte l’autre. Vous avez peut-être entendu l’expression « corrélation n’implique pas causalité ». La relation entre les variables peut s’expliquer de nombreuses façons.

Lignes de tendance

Les lignes de tendance dans les nuages de points vous aident à voir le schéma général de la relation et résument la forme générale des données. Dans notre exemple du prix de vente d’un logement et de la superficie, une ligne de tendance linéaire vous aide à identifier le schéma général de la relation.

Les relations ne sont pas toutes linéaires. Lorsque la forme de la relation est courbe, des lignes de tendance exponentielles ou logarithmiques peuvent remplacer le type linéaire.

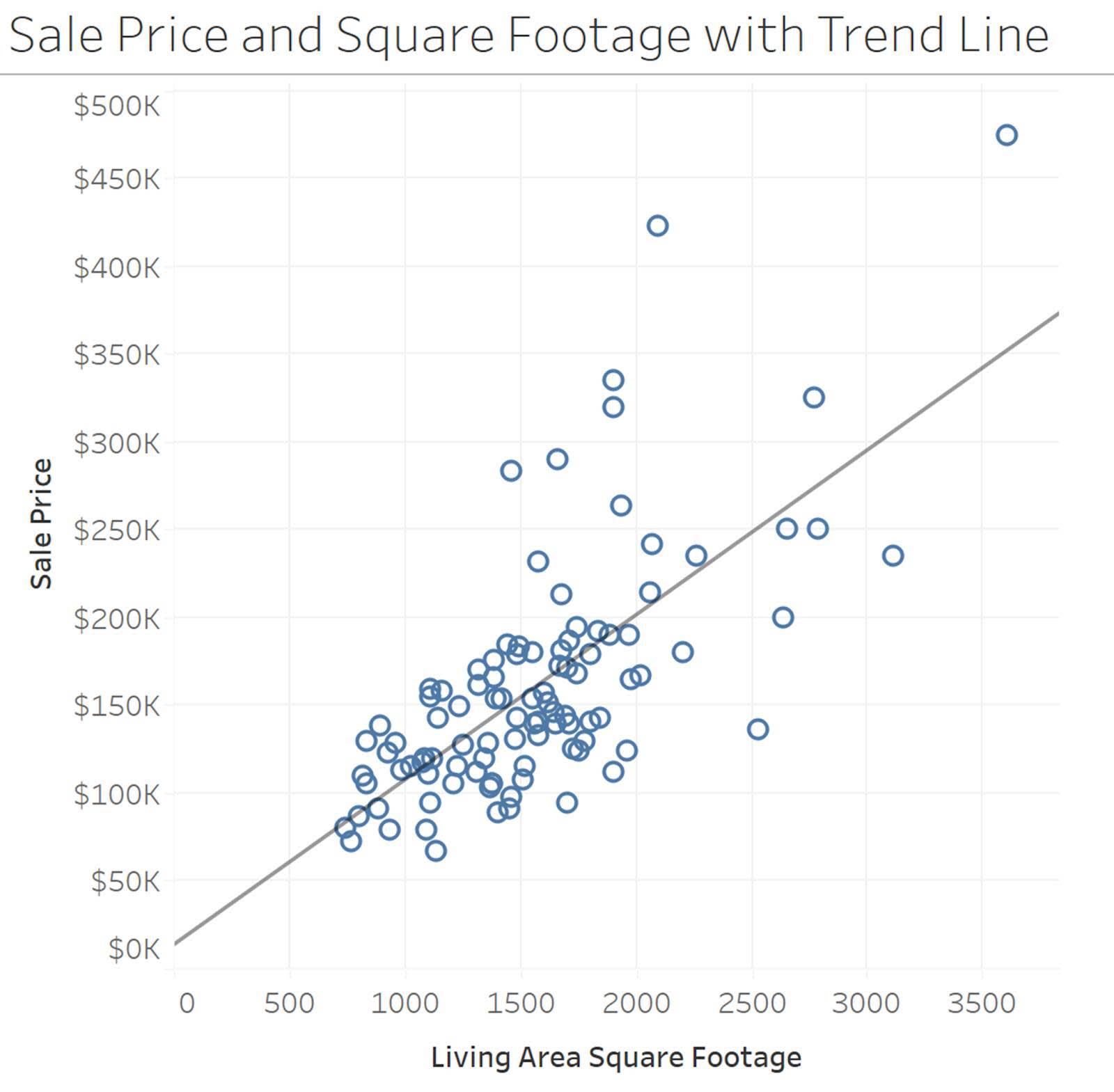
Consultez le module Corrélation et régression sur Trailhead pour en savoir plus sur la corrélation et la création d’une droite de régression linéaire.

Graphiques en bulles et perspectives de tableau

Les nuages de points précédents montraient la relation entre deux variables quantitatives, l’une sur l’axe x et l’autre sur l’axe y. Mais que faire lorsque l’on souhaite comparer plus de deux variables quantitatives ? Vous pouvez utiliser un autre attribut, à savoir l’attribut de taille, pour ajouter une troisième variable à un nuage de points.

Dans l’exemple suivant, le PIB par habitant et la couverture vaccinale sont représentés respectivement sur les axes x et y, la taille de chaque bulle représentant la taille de la population.

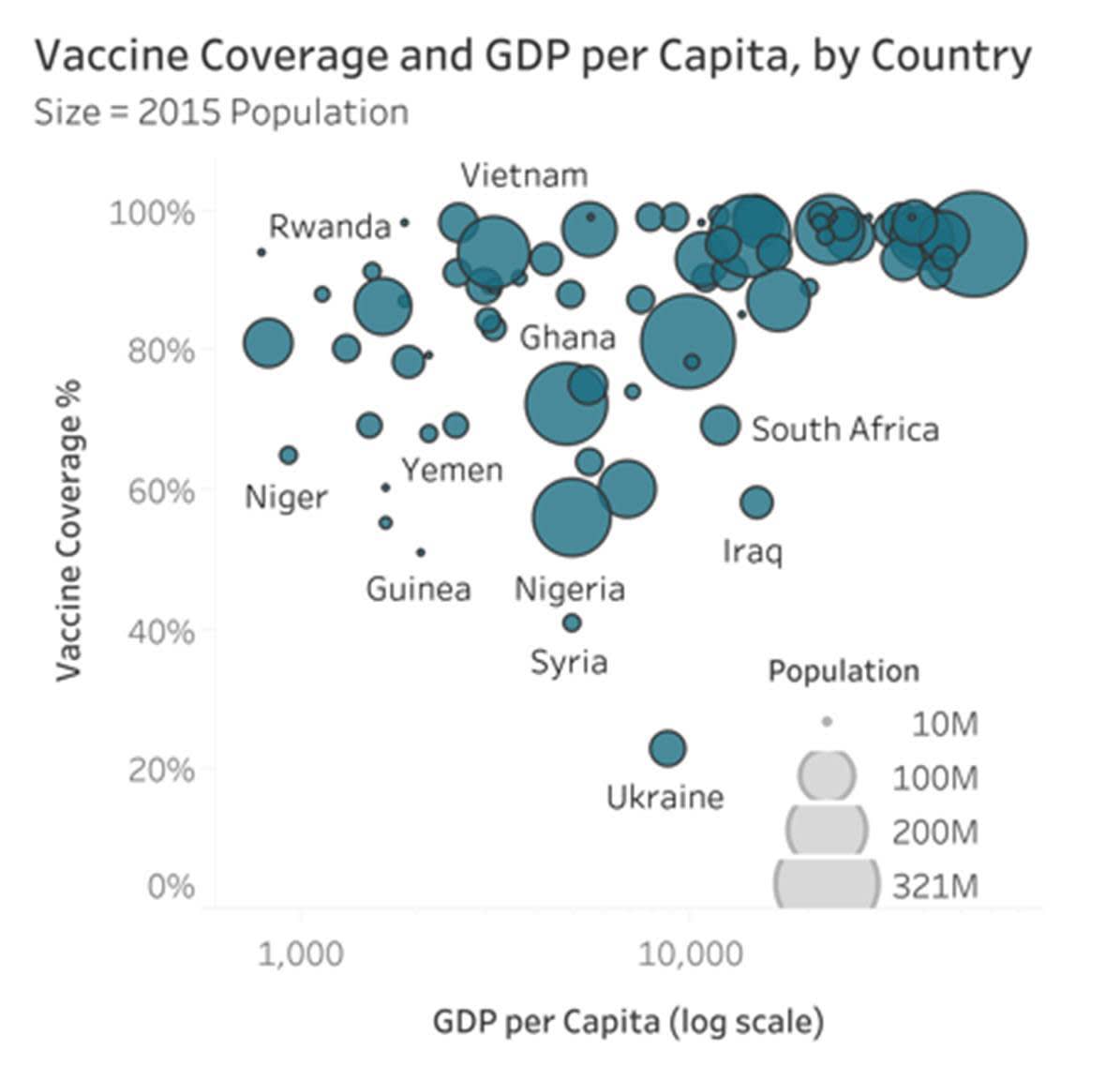
Vous avez appris précédemment dans ce module que les lecteurs ne perçoivent pas les différences de tailles quantitatives aussi précisément que d’autres attributs comme la longueur. Lorsque vous devez ajouter une troisième variable quantitative à un nuage de points, vous n’avez pas beaucoup d’autres options. C’est pourquoi l’utilisation de bulles de tailles différentes dans un nuage de points est une méthode acceptée. Si vous utilisez des bulles de tailles différentes, vous devez être conscient de la perte de précision de visualisation de la troisième variable.

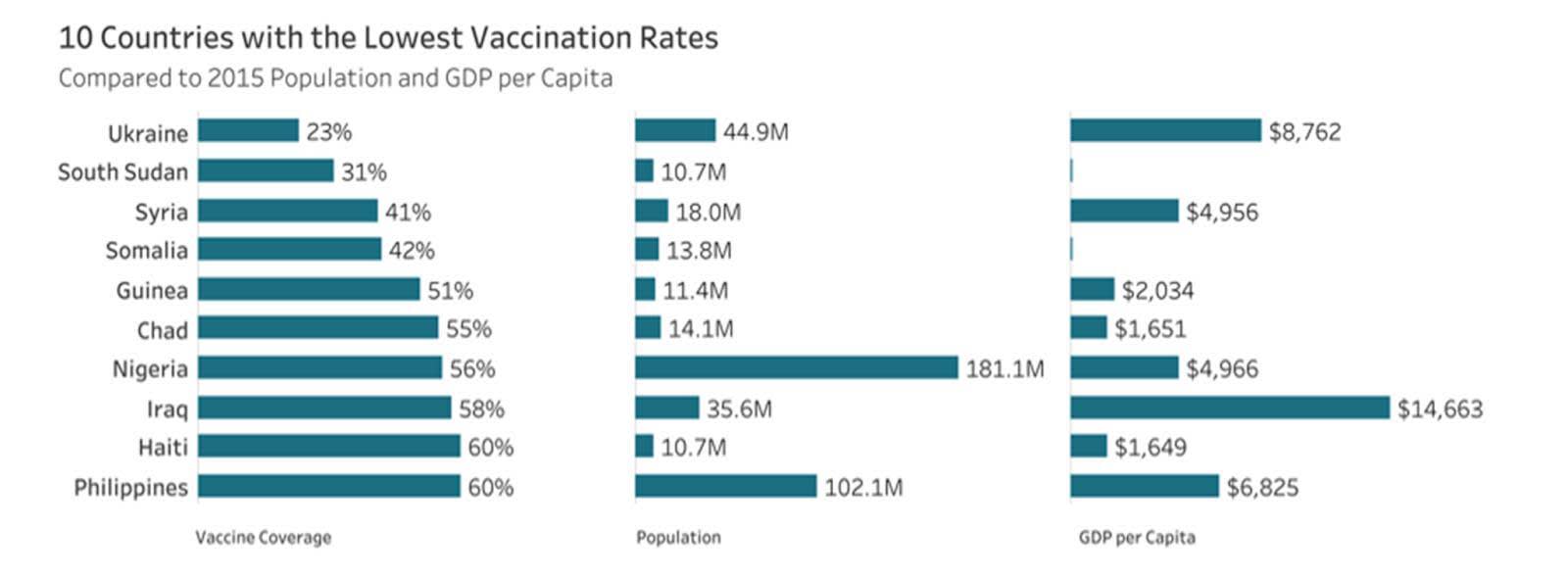
Lorsqu’il n’y a pas beaucoup de points de données ou que vous souhaitez uniquement comparer les valeurs supérieures ou inférieures de l’une des variables, les graphiques à barres peuvent venir à la rescousse sous la forme d’une perspective de tableau. La perspective de tableau permet de comparer au moins trois variables quantitatives à une variable qualitative (catégorielle) commune.

L’exemple montre les mêmes variables que le graphique en bulles illustré ci-dessus, sauf qu’il ne présente que les 10 pays ayant la couverture vaccinale la plus faible. La perspective de tableau vous permet également d’effectuer des comparaisons entre plusieurs métriques ou au sein d’une même métrique.

Ressources

• Site Internet du Financial Times : Charts that work: FT visual vocabulary guide
• Trailhead : Distributions des données
• Trailhead : Corrélation et régression
• Ouvrage : Introduction aux statistiques. Online Statistics Education: un domaine d’études multimédia interactif, 2020, par David M. Lane.
• Publication du blog de Sellers Dorsey : C’est l’histoire d’un histogramme et d’un polygone de fréquences…