Utilizar diagramas de caja y bigotes para mostrar distribuciones de variables continuas
Objetivos de aprendizaje
Después de completar esta unidad, podrá:
- Describir cómo se usan los diagramas de caja y bigotes para representar la distribución de datos.
- Crear un diagrama de caja y bigotes.
Hasta ahora, hemos explorado las diferentes maneras de visualizar las distribuciones de variables. En esta unidad, descubrirá otro gráfico importante, conocido como diagrama de caja y bigotes. Presentados en los años 1970 por el matemático estadounidense John Tukey, los diagramas de caja y bigotes representan un método visualmente conciso para ver y contrastar distribuciones de datos.
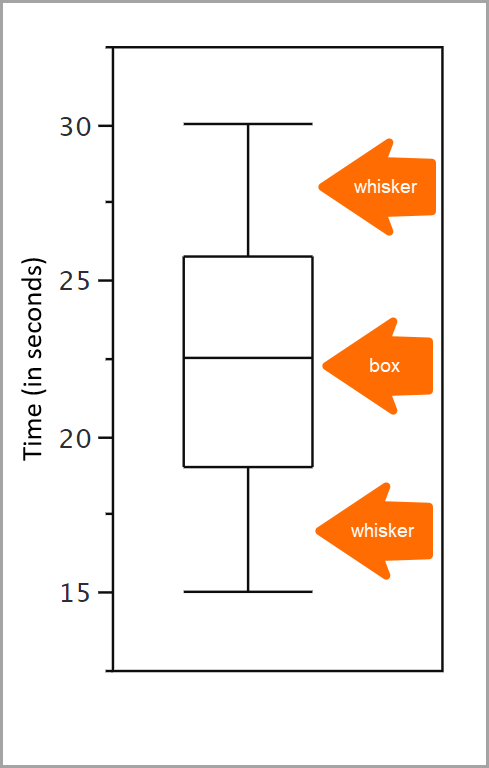
Las cajas en un diagrama de caja y bigotes muestran la mediana con el 50 % de los datos. Estos datos se extienden desde el percentil 25 hasta el percentil 75, con la mediana en el percentil 50.
Un percentil expresa una puntuación en comparación con otras puntuaciones dentro de un mismo conjunto de datos. Por ejemplo, imagine que resuelve una prueba para medir su nivel de timidez. En sí misma, su puntuación de timidez puede ser difícil de interpretar para usted. Quizás quiera comparar su puntuación con la de otros para conocer el porcentaje de personas con puntuaciones de timidez más bajas que la suya. Este porcentaje es un percentil. Si el 65 % de las otras personas que respondieron al cuestionario son menos tímidas que usted, su puntuación es el percentil 65.
Las cajas en un diagrama de caja y bigotes muestran la mediana con el 50 % de los datos, o los percentiles del 25 al 75. Pero, ¿qué ocurre con los datos que se quedan fuera? Aquí es donde entran en juego los bigotes. Los bigotes, que se muestran fuera de la caja, son líneas que terminan en un trazo horizontal. Proporcionan información sobre los valores que no están dentro de esa mediana con el 50 % de los datos (la caja), incluidos los valores atípicos. Los valores atípicos pueden entenderse como observaciones poco frecuentes o como valores que tienen una desviación extrema del centro de una distribución.
Veremos todos estos conceptos con más detalle más adelante en la unidad.
Crear un diagrama de caja y bigotes
El siguiente ejemplo de un diagrama de caja y bigotes fue adaptado del capítulo de David M. Lane sobre el tema, que está disponible en Online Statistics Education: A Multimedia Course of Study. Líder del proyecto: David M. Lane, Rice University.
El autor realizó un experimento en una clase de 31 estudiantes. Cada estudiante recibió una página con 30 rectángulos de colores y su tarea consistía en nombrar los colores lo más rápido posible.
En la siguiente tabla se muestran sus tiempos, en segundos.
|
14 |
17 |
18 |
19 |
20 |
21 |
|
15 |
17 |
18 |
19 |
20 |
22 |
|
16 |
17 |
18 |
19 |
20 |
23 |
|
16 |
17 |
18 |
20 |
20 |
24 |
|
17 |
18 |
18 |
20 |
21 |
24 |
| 29 |
Vamos a utilizar este conjunto de datos para crear un diagrama de caja y bigotes. Esta es una descripción general de los pasos que debe seguir para crear uno.
- Calcular los percentiles.
- Trazar la caja según los percentiles.
- Determinar el tamaño del paso.
- Agregar los bigotes.
- Agregar el valor exterior.
Calcular percentiles
Recuerde que las cajas en los diagramas de caja y bigotes abarcan desde el percentil 25 hasta el percentil 75 de los datos. El percentil 50 se incluye dentro de la caja. La parte inferior de la caja (llamada bisagra inferior) es el percentil 25 y la parte superior de la caja (llamada bisagra superior) es el percentil 75.
En los siguientes pasos, vamos a utilizar una línea numérica para ver los percentiles.
-
Enumere las puntuaciones de menor a mayor.

-
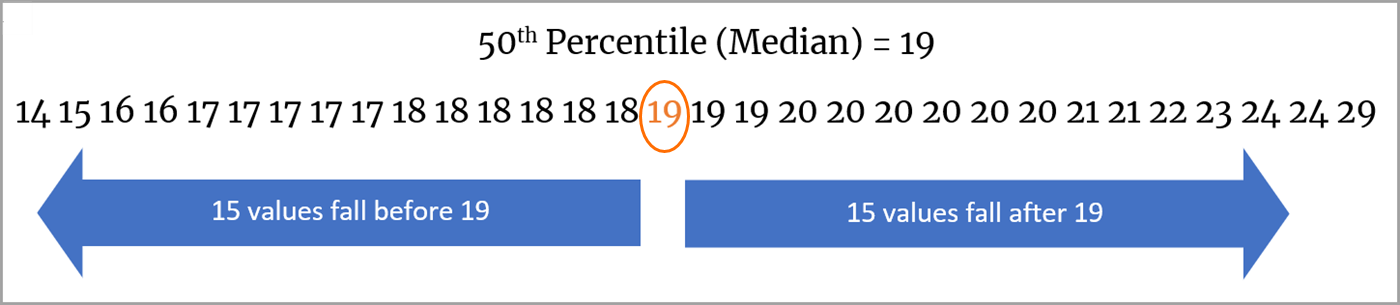
Determine la mediana, o el valor central. El valor de la mediana se ubica en la mitad, entre el inicio y el final de la secuencia de números. En una secuencia de 31 valores, al posicionarnos en el medio, tendremos 15 valores antes de la mediana y 15 valores después de ella. Por lo tanto, el valor de la mediana es 19.
-
Determine el percentil 25. El valor del percentil 25 se ubica en el medio, entre el inicio de la secuencia y el valor de la mediana. En nuestro ejemplo de 31 valores, la ubicación intermedia tiene 7 valores antes y 7 valores entre ella y la mediana. Por lo tanto, el valor del percentil 25 es 17.

-
Determine el percentil 75. El valor del percentil 75 se ubica en el medio, entre la mediana y el final de la secuencia. En nuestra lista de 31 valores, la ubicación intermedia tiene 7 valores entre ella y la mediana, y 7 valores entre ella y el final de la secuencia. Por lo tanto, el valor del percentil 75 es 20.

Trazar la caja según los percentiles
Vamos a reunir estos valores y trazar la caja.
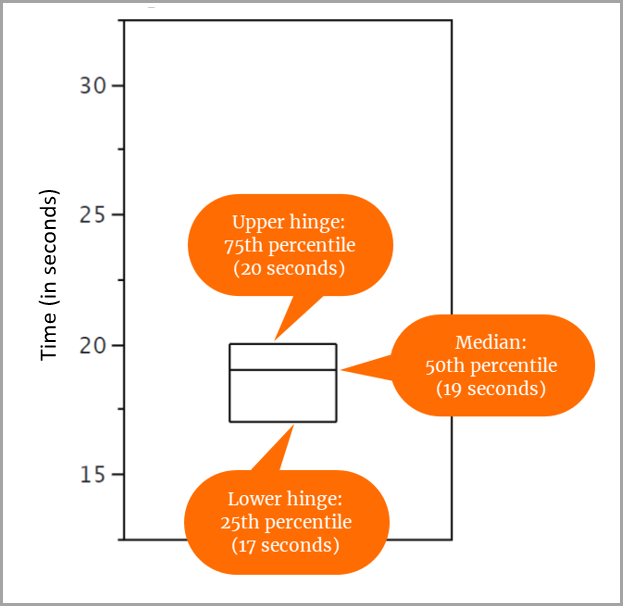
Para nuestro conjunto de 31 puntuaciones, hemos determinado lo siguiente:
- El percentil 25 es 17.
- El percentil 50 ( o mediana) es 19.
- El percentil 75 es 20.
Por lo tanto, la caja se traza de la siguiente manera:
- El percentil 25 (bisagra inferior) está alineado con el valor 17 del eje Y.
- El percentil 50 (mediana) está alineado con el valor 19 del eje Y.
- El percentil 75 (bisagra superior) está alineado con el valor 20 del eje Y.
La mediana con el 50 % de los valores de los datos aparece en la caja.
Determinar el tamaño del paso
Ahora puede prepararse para trazar bigotes arriba y debajo de la caja a fin de proporcionar información adicional sobre la distribución de los datos. La ubicación de los bigotes está determinada por los pasos. Un paso se define como 1,5 x ReC. ReC es el rango entre cuartiles.
Aunque esto pueda parecer complejo, el ReC simplemente hace referencia a la diferencia entre el valor de la bisagra superior (percentil 75) y el valor de la bisagra inferior (percentil 25). Recuerde que la mediana con el 50 % de los valores de los datos aparece en la caja delimitada por esos valores.
En nuestro conjunto de puntuaciones, el valor de la bisagra superior es 20 y el valor de la bisagra inferior es 17. Por lo tanto, el ReC es 20 menos 17, es decir, 3.
A fin de determinar el tamaño del paso, multiplicamos 3 (el ReC) por 1,5 y obtenemos 4,5 como tamaño del paso.
Agregar los bigotes
Para comprender cómo se trazan los bigotes, primero vamos a ver algunos términos y de qué manera se aplican a las puntuaciones en nuestro ejemplo.
¿Dónde se trazan los bigotes?
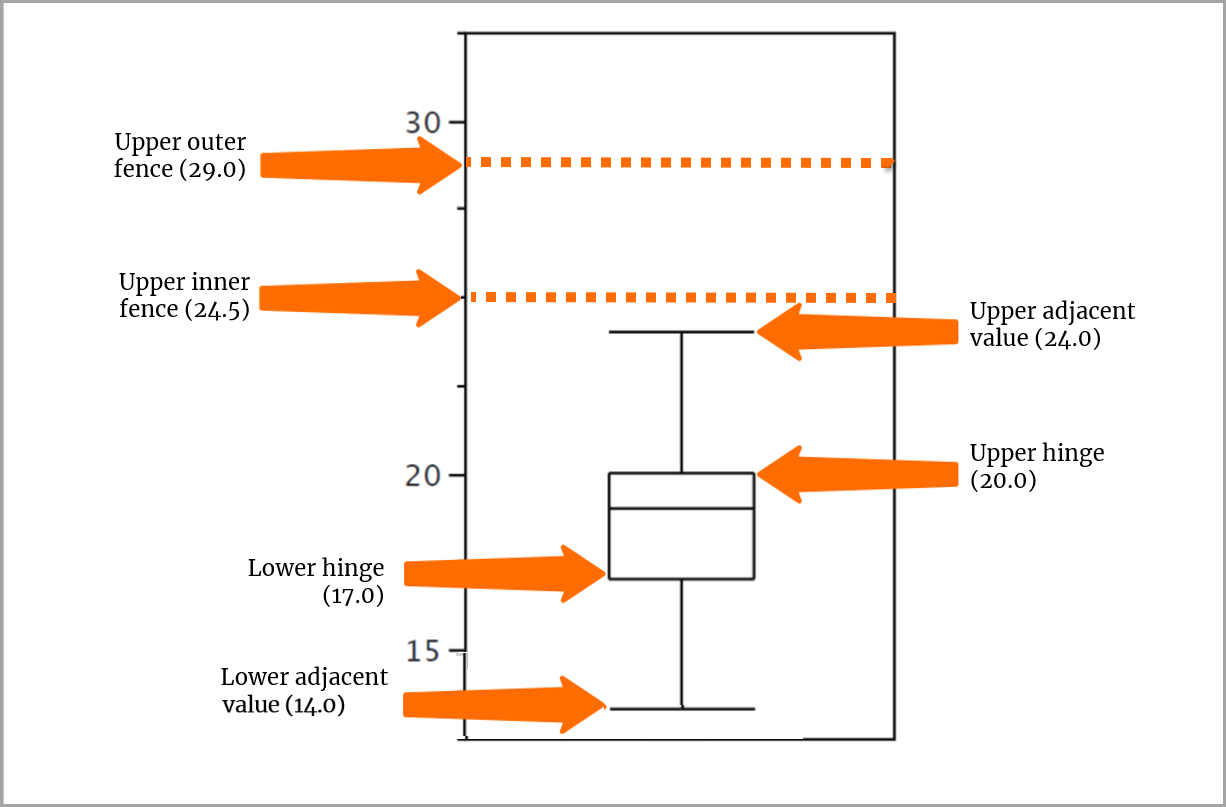
Puede trazar los bigotes desde la bisagra superior hasta el valor adyacente superior y desde la bisagra inferior hasta el valor adyacente inferior.
Los bigotes no llegan por completo a los valores exteriores. En su lugar, se representa un valor exterior con una o pequeña, y un valor lejano con un asterisco (*).
En nuestros datos de puntuación, los bigotes van desde el valor de la bisagra superior (20) hasta el valor adyacente superior (24) y desde el valor de la bisagra inferior (17) hasta el valor adyacente inferior(14).
Agregar el valor exterior
Un valor exterior es un valor que va más allá del límite interior, pero no más allá del exterior. Tenemos uno de estos valores en nuestro conjunto de puntuaciones, 29, que coincide con el valor del límite exterior, pero no va más allá de él. Se utiliza una pequeña o para representar este valor.
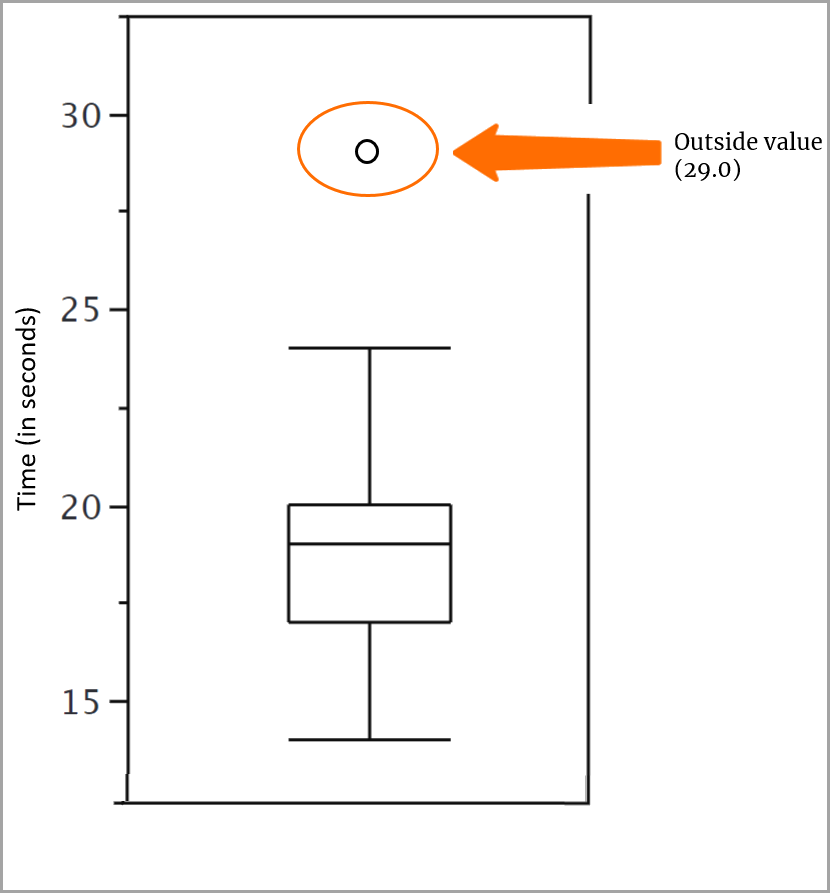
Y con esto, su diagrama de caja y bigotes está completo.
Diagramas de caja y bigotes e histogramas
Es posible que se esté preguntando en qué se diferencian los diagramas de caja y bigotes de los histogramas a la hora de mostrar distribuciones.
- Los histogramas utilizan agrupaciones para trazar la frecuencia de los valores.
- En los diagramas de caja y bigotes, la mediana con el 50 % de los datos aparece en la caja, mientras que los valores atípicos (si los hay) se trazan fuera de los bigotes.
Para hacerse una idea de cómo funciona, volvamos a los datos que muestran las formas de las distribuciones de alturas. Compare cómo se ven los datos en un histograma y en un diagrama de caja y bigotes.
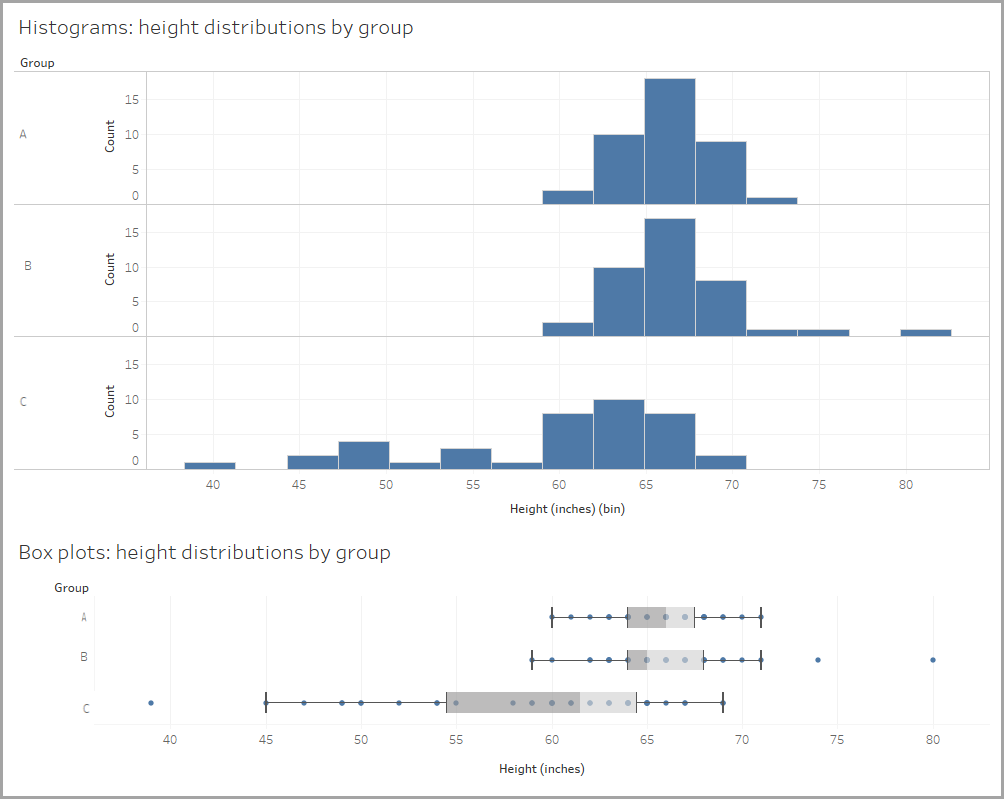
Puede observar que los diagramas de caja y bigotes utilizan mucho menos espacio. Esto puede facilitar la comparación de distribuciones. Tres distribuciones situadas una al lado de la otra son más fáciles de comparar con diagramas de caja y bigotes que con histogramas. Vamos a ver algunos ejemplos más.
Ahora ya sabe cómo las distribuciones pueden ayudarlo a explorar y comprender los datos, y a comunicarse con ellos.
