Estimar la probabilidad
Objetivos de aprendizaje
Después de completar esta unidad, podrá:
- Describir las distribuciones continuas.
- Describir las características de una distribución normal.
Introducción
En el módulo Distribuciones de datos, se explica que puede usar un histograma para representar la distribución de valores continuos. A continuación, exploremos el concepto de distribuciones continuas.
No abordaremos las fórmulas específicas utilizadas para realizar los cálculos mencionados en esta unidad. Sin embargo, conocer los aspectos generales de estos conceptos puede resultarle útil a medida que explora y comprende los datos, y se comunica con ellos.
Curvas de densidad
En el módulo Distribuciones de datos, se explica cómo los histogramas pueden representar las distribuciones de muestras finitas de variables continuas. La altura de cada barra en el histograma es proporcional a la frecuencia de los valores dentro de esa agrupación. En otras palabras, cuanto más alta sea la barra, con más frecuencia los puntos de datos de la muestra estarán dentro de esa agrupación.

Por ejemplo, en el histograma anterior se muestra la distribución de la altura, en pulgadas, para 40 personas. Claramente, se trata de una muestra con un número finito de puntos de datos. Sin embargo, al considerar todos los posibles valores de la variable continua de la altura, es evidente que puede variar mucho. No hay horas suficientes en nuestros ciclos de vida para crear un histograma con agrupaciones para todos los valores de altura posibles. Lo mismo ocurre con cualquier otra variable continua.
En lugar de usar un histograma para representar todos los valores posibles de una variable continua, podemos usar una distribución continua. Una distribución continua tiene el aspecto de una curva suave, también llamada curva de densidad. La curva de densidad representa más que simplemente los valores de una muestra específica. Representa todos los valores posibles, así como sus probabilidades de ocurrencia o la probabilidad de que ocurran los valores.
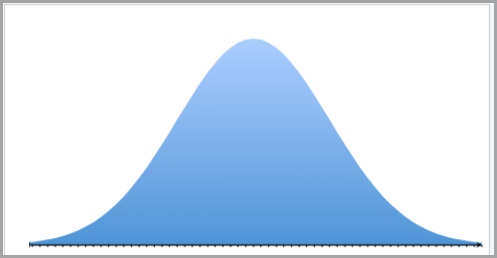
Al mirar los histogramas, usamos la altura de las barras para comprender la cantidad de puntos de datos que existen dentro de esa agrupación, o con qué frecuencia los puntos de datos están dentro de esa agrupación. Sin embargo, cuando observamos distribuciones continuas, no podemos interpretar la altura de una curva de probabilidad de esa manera.
Piense en los datos con todos los valores de altura posibles. No es relevante conocer la probabilidad de que una persona mida exactamente 61 pulgadas. Con un número infinito de valores, hacer una pregunta centrada en 61 pulgadas es tan arbitrario como preguntar sobre la probabilidad de que alguien mida 61,002 pulgadas o 60,9997 pulgadas.
En su lugar, la probabilidad se analiza con un intervalo, que equivale al área bajo la curva dentro de ese intervalo.
El área total bajo la curva es 1 o un 100 %, porque hay un 100 % de probabilidad de que todos los valores posibles estén en algún lugar dentro de la curva.

En resumen, estos son algunos conceptos que debe tener en cuenta sobre las curvas de densidad.
- El área total bajo la curva es un 100 % o 1.
- Son distribuciones continuas que representan todos los puntos de datos posibles a la vez.
- El eje Y representa la densidad de probabilidad, que indica la posibilidad de obtener valores cerca de los puntos correspondientes en el eje x.
Distribución normal
Ahora nos centraremos en una curva de densidad especial, la distribución normal o curva normal. Tiene la forma simétrica de una campana.
Al observar las distribuciones de variables continuas expresadas gráficamente en histogramas, aprendió a identificar una distribución simétrica. Si dobla un histograma distribuido simétricamente por la mitad, ambos lados coincidirían perfectamente. En las distribuciones simétricas, la media y la mediana son iguales.
Al igual que sucede en las distribuciones simétricas, en una distribución normal, la forma es simétrica y la media también es igual a la mediana.
Estas son las principales características de una distribución normal.
- Son simétricas alrededor de la media.
- La media y la mediana son iguales.
- El área bajo la curva normal es igual a 1,0 (o un 100 %).
- Son más densas en el centro y menos densas en los extremos.
- Se definen en función de dos parámetros, la media y la desviación estándar.

Observe la distribución normal que se muestra en la curva de arriba. En una distribución normal, el 68 % de los datos se encuentran entre una desviación estándar de +1 y -1 respecto de la media, y el 95 % de los datos se encuentran dentro de unas desviaciones estándar de -2 y +2 respecto de la media. Los extremos cortos a ambos lados de la curva indican que muy pocos valores (un 5 %) estarán fuera de las desviaciones estándar de -2 y +2 respecto de la media.
Las distribuciones normales con desviaciones estándar más pequeñas tendrán curvas más estrechas y altas que las distribuciones normales con desviaciones estándar más grandes.
En esta imagen, ambas distribuciones normales tienen una media de 50. La curva más grande tiene una desviación estándar de 5 y la curva más pequeña tiene una desviación estándar de 10.

Utilidad de la distribución normal
En su libro El arte veraz (en inglés), el diseñador de información y profesor Alberto Cairo explica que “ningún fenómeno en la naturaleza sigue una distribución normal perfecta, pero muchos se aproximan lo suficiente como para convertirla en una de las principales herramientas de la estadística”. Cairo sigue explicando: “Si sabe que el fenómeno que está estudiando tiene una distribución normal, aunque no sea perfecta, puede estimar la probabilidad de cualquier caso o puntuación con una precisión razonable.” En otras palabras, las propiedades de la curva normal se pueden utilizar para estimar la probabilidad de un caso o una puntuación con una precisión razonable.
En general, las estimaciones de una población derivan de una muestra, porque no siempre podemos medir la población completa. Si la muestra representa a la población, la curva normal es una herramienta de estimación útil.

Intervalos de confianza
Al usar la curva normal para hacer estimaciones de probabilidad en datos de muestra, puede usar intervalos de confianza a fin de incluir un margen de error.
Los intervalos de confianza son un ejemplo de inferencias. La inferencia es un proceso que implica extraer conclusiones sobre una población a partir de una muestra de los datos.

Un intervalo de confianza contiene una media poblacional para una proporción específica del tiempo. Por ejemplo, si desea tener un intervalo de confianza del 95 %, significa que en ese intervalo del 95 % de sus datos se incluirá la media real.
El intervalo de confianza del 95 % se obtiene con la distribución normal, donde el 95 % de los fatos se encuentran entre -2 y +2 de desviación estándar de la media.
Exploremos el siguiente ejemplo adaptado del capítulo de David M. Lane sobre intervalos de confianza, disponible para el público en su trabajo en línea Introducción a la estadística.
Imagine que desea conocer el peso medio (promedio), en libras, de los niños de 10 años en los Estados Unidos. Obviamente, no puede pesar a cada niño de 10 años, así que, pesa a una muestra de 16 niños. Descubre que el peso medio es de 40,8 kg. Esta media de la muestra de 40,8 kg es una estimación puntual de la media de la población. Sin embargo, no brinda una idea clara de cuán cerca o lejos está de la media de la población. En otras palabras, ¿puede afirmar que el peso medio de toda la población estadounidense de niños de 10 años está dentro de los 2,3 kg de 40,8 kg? Simplemente, no tiene cómo saberlo.

Sin embargo, puede usar un cálculo para lograr un intervalo de confianza del 95 %. Nota: El cálculo no se explica aquí. Un intervalo de confianza del 95 % incluiría pesos medios de entre 33 y 48,6 kg.
En otras palabras, sería razonable afirmar que el peso medio de toda la población de niños estadounidenses de 10 años estaría entre 33 y 48,6 kg. Esto se debe a que, después de tomar muestras repetidas con el intervalo de confianza del 95 % calculado para cada muestra, el 95 % de las veces, los intervalos incluyen la media real.
Pero esto también indica que, en el 5 % de los casos, los intervalos no incluyen la media real.
Ejemplos reales de visualización de la incertidumbre
Alberto Cairo, mencionado anteriormente en esta unidad, también escribió una serie de publicaciones de blog donde describe ejemplos reales de cómo se ha representado (y malinterpretado) la incertidumbre en visualizaciones que ilustra las trayectorias de los huracanes. Puede explorar la publicación del blog sobre la mala interpretación de los mapas del pronóstico para la tormenta de categoría 5 en 2019, el huracán Dorian, además de otros temas relacionados, en el sitio web profesional de Alberto Cairo.
Ya conoce las distribuciones continuas, incluida la forma especial de la curva normal. En la próxima unidad, analizaremos el concepto de pruebas de hipótesis con muestras de datos.
Recursos
- Sitio web: Educación sobre estadística en línea de David M. Lane: Curso de estudio multimedia interactivo, 2020.
- Sitio web: Sitio web profesional de Alberto Cairo