Hacer comparaciones correlativas, de desviaciones y distribuciones

Objetivos de aprendizaje

Después de completar esta unidad, podrá:

• Describir las comparaciones correlativas, de desviaciones y de distribuciones.
  
• Comprender las mejores prácticas para hacer comparaciones con gráficos.
  

Desviación

Las comparaciones de desviaciones se centran en lo que los valores se diferencian de un valor inicial, a veces un valor promedio o umbral.

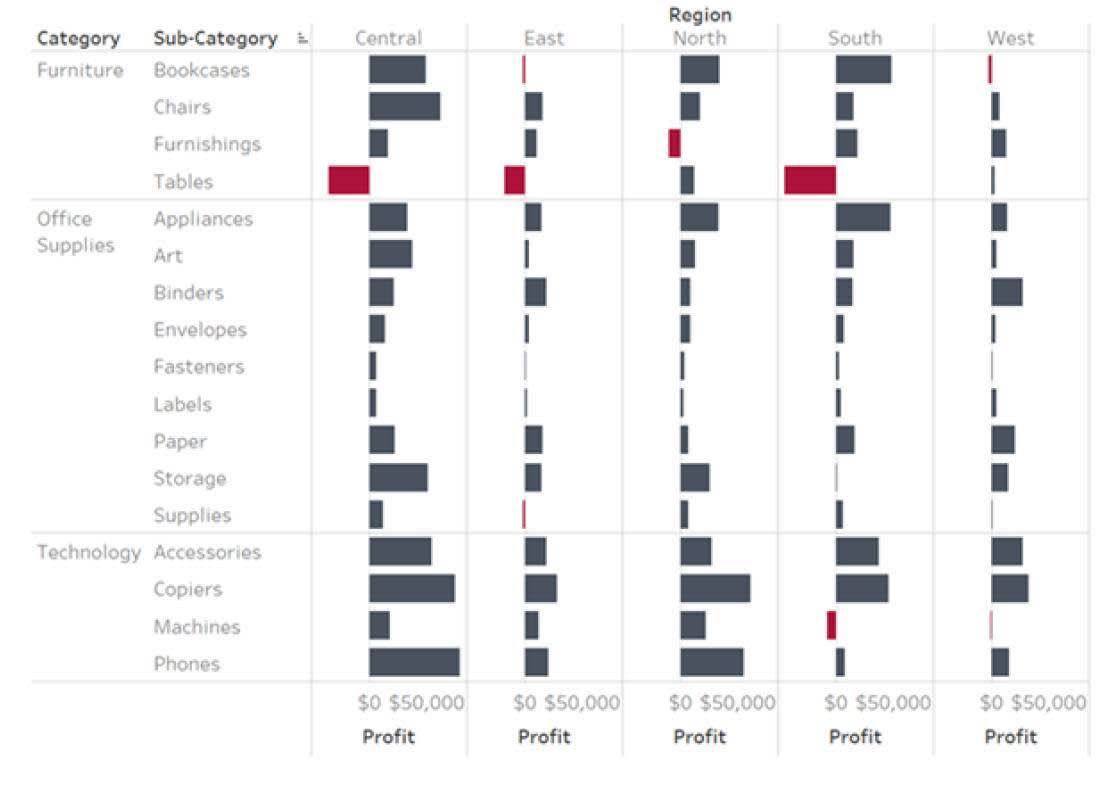
Gráficos de barras divergentes

En el ejemplo, la longitud de las barras muestra la distancia de un valor central de cero para indicar la cantidad de ganancias o pérdidas. Se puede ver rápidamente qué elementos y regiones no son rentables.

Gráficos de líneas

Anteriormente, aprendió que los gráficos de líneas son una de las mejores maneras de mostrar un cambio en los valores a lo largo del tiempo. De la misma manera, cuando quiera mostrar la desviación a lo largo del tiempo, un gráfico de líneas es una buena opción. En el siguiente ejemplo, se muestra el cambio porcentual del volumen interanual de pacientes de la sala de emergencias por cada mes entre 2015 y 2016. Se puede ver que en junio se dio el mayor incremento en volumen de pacientes desde el año anterior.

Distribuciones

Una distribución muestra todos los valores de datos posibles y la frecuencia (conteo) con la que aparecen. En otras palabras, una distribución describe cuántas veces aparece un valor de datos en un conjunto de datos.

Histogramas

¿Usó alguna vez una aplicación de mapas en su teléfono para descubrir las horas pico en su restaurante favorito? Es posible que haya prestado atención al gráfico que muestra las horas pico. Este gráfico es un histograma. El pico muestra la hora de más concurrencia.

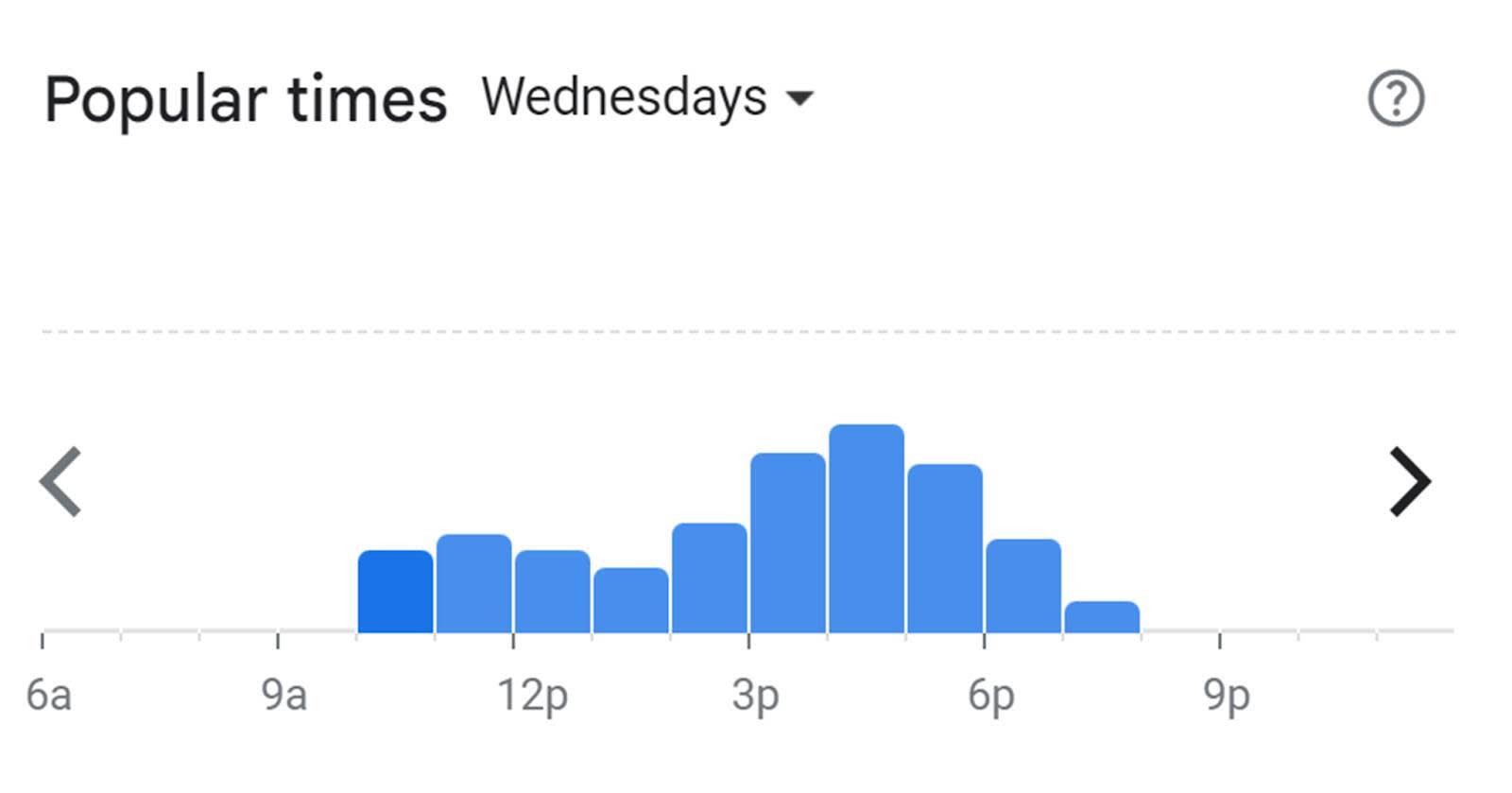
Un histograma es similar a un gráfico de barras, pero agrupa valores cuantitativos en rangos del mismo tamaño, o agrupaciones. Se cuentan cuántos valores hay en cada agrupación para mostrar en el histograma. Cuando se usan programas como Tableau, el programa determina automáticamente el tamaño de la agrupación y proporciona la frecuencia (o conteo) de los valores en cada agrupación.

En el siguiente ejemplo, el histograma ofrece una vista detallada de los valores de precios de ventas de viviendas para todo el conjunto de datos. Se puede ver que la mayoría de las casas se venden a un precio de entre USD 100 000 y USD 200 000. El histograma también muestra que hay algunas viviendas con precios más altos, si se las compara con la mayoría de las viviendas.

A veces, las distribuciones pueden presentarse como porcentajes en lugar de recuentos o frecuencias.

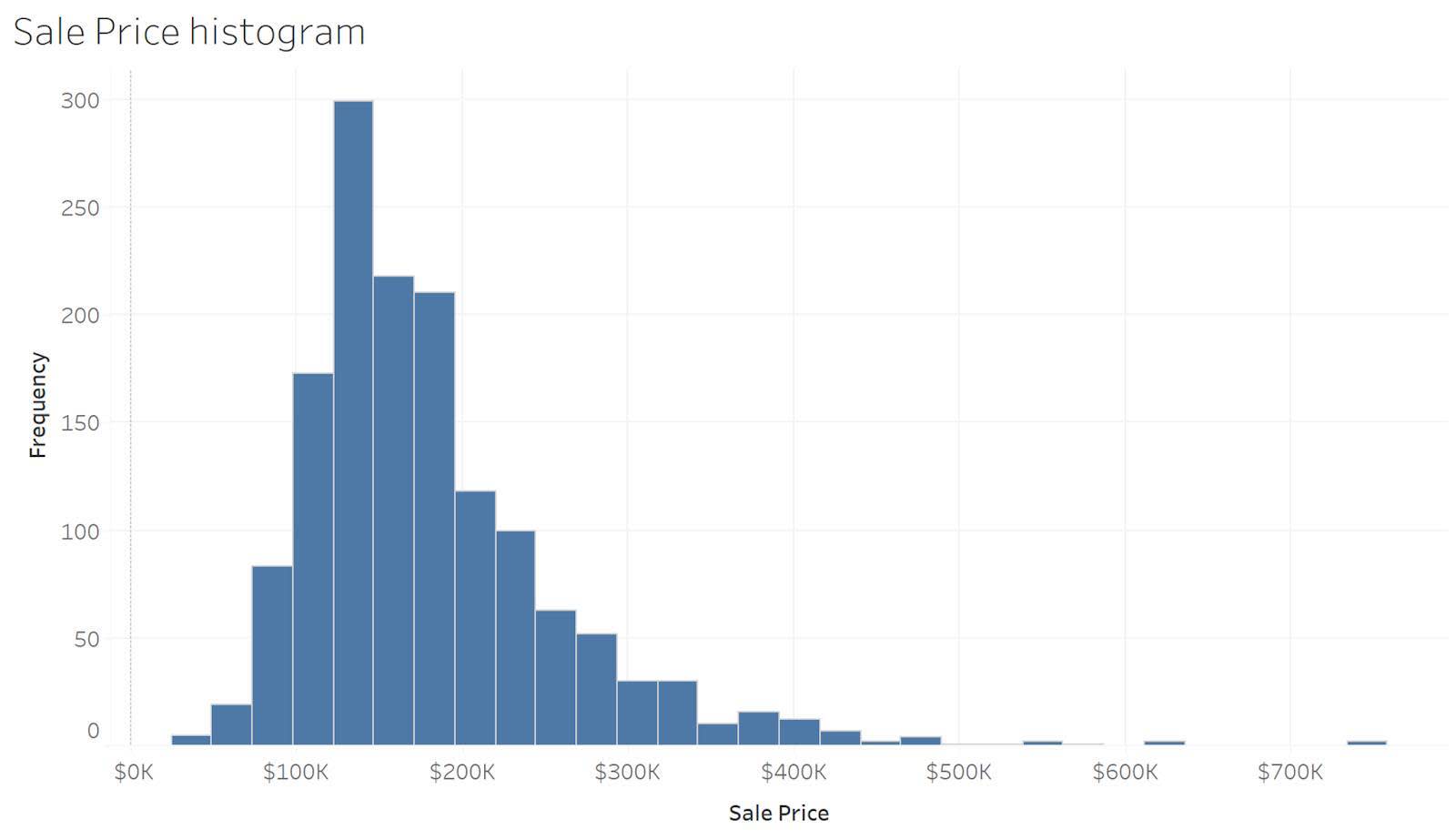
Polígonos de frecuencia

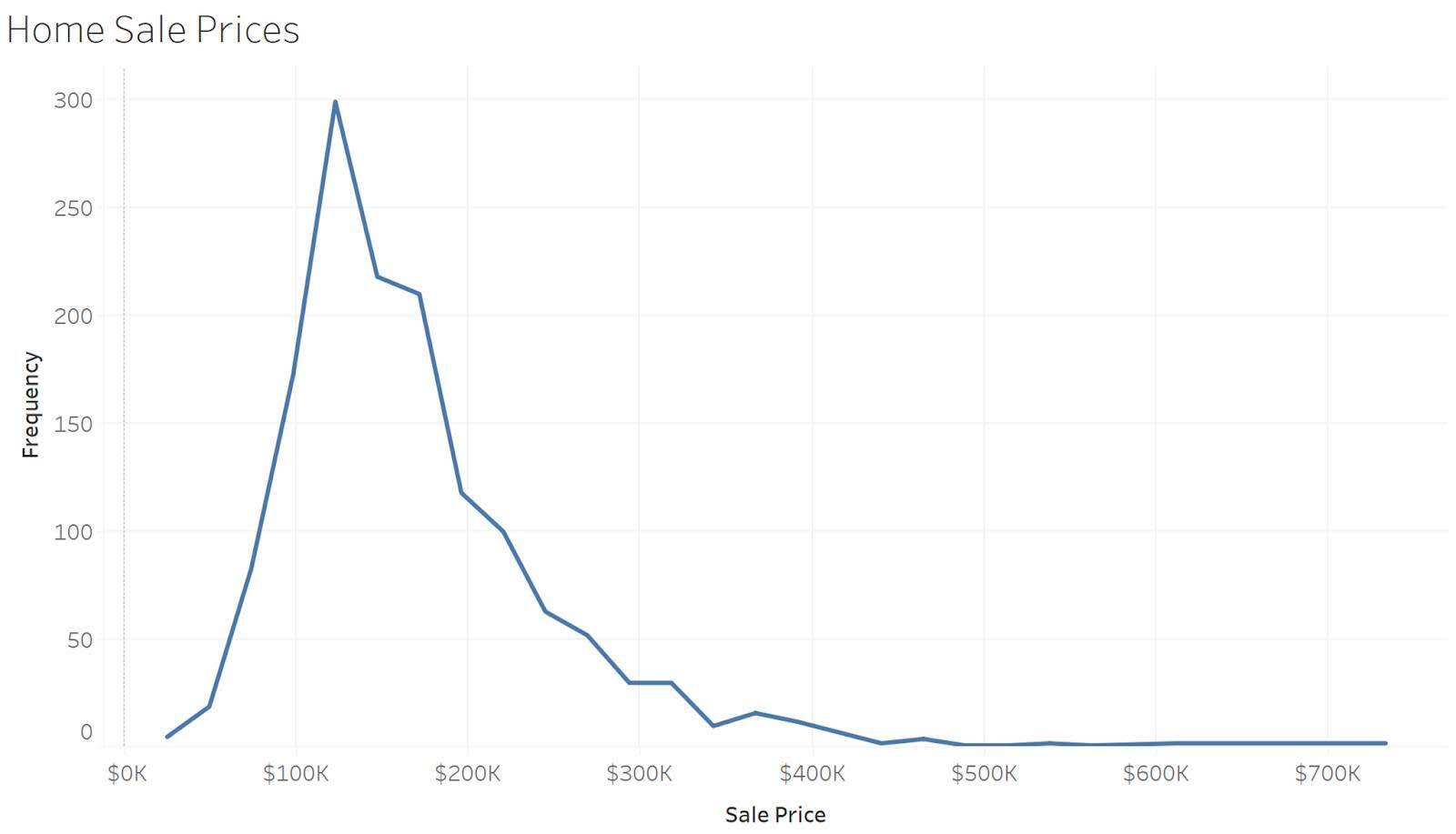
Los polígonos de frecuencia son parecidos a los histogramas, pero utilizan líneas para conectar los recuentos de frecuencia. En el siguiente ejemplo se muestran los mismos datos que en el histograma anterior, pero los recuentos en cada agrupación están conectados con una línea. La línea ofrece una vista más simple y clara para el lector.

Utilice polígonos de frecuencia en lugar de histogramas cuando quiera mostrar más de una distribución en el mismo gráfico.

Diagramas de bandas

Los diagramas de bandas muestran un punto por cada valor de dato en una línea y ocupan mucho menos espacio que los histogramas o los polígonos de frecuencia. Resultan eficientes a la hora de mostrar el rango de una distribución y si hay agrupaciones en clústeres de valores. Si muchos valores son iguales, o muy cercanos entre sí, se ubican unos encima de otros, lo cual dificulta la distinción de los valores que aparecen con frecuencia en los datos.

En el siguiente ejemplo, que utiliza los mismos datos que el histograma, se puede ver que, aunque el diagrama de bandas permite ver con facilidad las viviendas con precios más elevados, resulta difícil visualizar los precios de venta más frecuentes. Por lo tanto, es mejor usar diagramas de bandas cuando los conjuntos de datos son más pequeños.

Hacer que los puntos de un diagrama de bandas sean transparentes permite que varios puntos aparezcan más oscuros y que el lector distinga entre valores únicos y varios valores similares.

Diagramas de caja y bigotes

Los diagramas de caja y bigotes muestran las distribuciones de manera más compacta que un histograma. Cuando se comparan varias distribuciones, los diagramas de caja y bigotes comparan distribuciones entre categorías de manera eficiente. La caja de un diagrama de caja y bigotes muestra el 50 % medio de los datos (o el percentil 25 a 75) e incluye una línea que muestra el valor medio (o percentil 50).

¿Pero qué ocurre con los datos que quedan afuera? Ahí entran en juego los bigotes: se trazan fuera de la caja y representan líneas verticales que terminan en un trazo horizontal. Brindan información sobre los valores que no se encuentran dentro del 50 % medio de los datos (la caja), y ofrecen un límite para distinguir los valores atípicos. Los valores atípicos pueden entenderse como observaciones atípicas y poco frecuentes, o bien como valores que tienen una desviación extrema respecto del centro de una distribución.

En los diagramas de caja y bigotes, existen distintas maneras de calcular el límite donde deberían estar los valores atípicos potenciales. Algunos programas indican los valores atípicos extremos con un símbolo diferente si estos valores están más allá del límite típico.

En el siguiente ejemplo se comparan las distribuciones de los precios de venta de viviendas para distintos tipos de edificios. Se puede observar que las viviendas unifamiliares tienen un rango de valores mucho mayor que el de los demás tipos de edificios, lo que incluye las viviendas de mayor precio que parecen ser valores atípicos.

En este ejemplo de diagramas de caja y bigotes también se incluyen diagramas de bandas verticales para mostrar cada valor individual. Ahora puede visualizar todos los puntos de datos y detalles sobre la distribución en un mismo gráfico. Aunque puede tomar un tiempo aprender a leer diagramas de caja y bigotes, pueden proporcionar mucha información sobre una distribución sin ocupar demasiado espacio.

Consulte el módulo Distribuciones de datos en Trailhead para obtener más información sobre las distribuciones.

Correlaciones

Las comparaciones correlativas exploran la relación entre variables cuantitativas. Responden preguntas como “¿Una variable aumenta o se reduce con otra variable?”.

En estadística, el término “correlación” puede tener significados específicos. Por ejemplo, al hablar de coeficientes de correlación, nos referimos a un tipo específico de relación entre variables cuantitativas, generalmente lineal. En el módulo Correlación y regresión, encontrará información sobre cómo realizar análisis de correlación y regresión.

Diagramas de dispersión

Los diagramas de dispersión se utilizan para mostrar la relación entre dos variables cuantitativas. Una variable se muestra en el eje X y la otra, en el eje Y. Los diagramas de dispersión pueden mostrar si hay una relación entre las variables. Por ejemplo, si una variable “va en la misma dirección” que otra y qué tipo de relación existe (lineal u otro patrón).

Visualizar diagramas de dispersión también ayuda a ver los valores atípicos. En el siguiente ejemplo, se muestra la relación entre el precio de venta de viviendas y la superficie del área de estar. Cada punto del diagrama de dispersión representa una vivienda con el precio de venta en el eje Y y la superficie en el eje X.

A pesar de que un diagrama de dispersión puede mostrar la relación entre dos variables, no prueba que una variable afecta a la otra. Es posible que haya oído el dicho: “La correlación no prueba la causalidad”. La relación entre las variables se puede generar por muchos motivos.

Líneas de tendencia

Las líneas de tendencia en los diagramas de dispersión ayudan a ver el patrón general de la relación y resumen la forma general de los datos. En nuestro ejemplo del precio de venta de las viviendas y la superficie, una línea de tendencia lineal ayuda a ver el patrón general de la relación.

No todas las relaciones son lineales. Cuando la forma de la relación es curva, se pueden usar líneas de tendencia exponenciales o logarítmicas, en lugar de lineales.

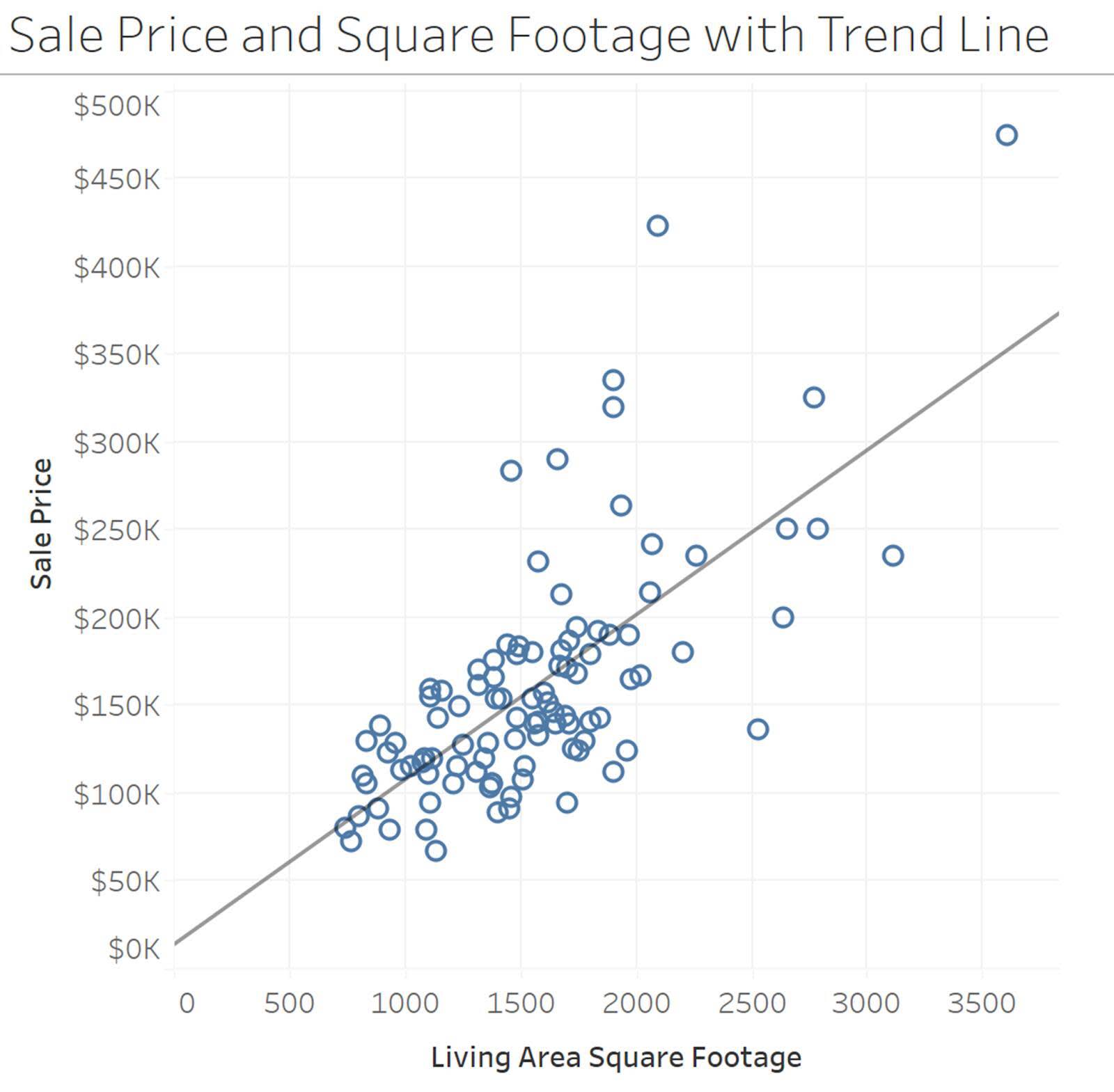
Consulte el módulo Correlación y regresión en Trailhead para obtener más información sobre las correlaciones y la creación de una línea de regresión lineal.

Diagramas de dispersión con burbujas de diferentes tamaños y lente de tabla

Los diagramas de dispersión anteriores muestran la relación entre dos variables cuantitativas. Una variable se muestra en el eje X y la otra, en el eje Y. Pero ¿qué debe hacer cuando quiere comparar más de dos variables cuantitativas? Puede usar otro atributo, tamaño, para agregar una tercera variable a un diagrama de dispersión.

En el siguiente ejemplo, se muestran el PIB per cápita y la cobertura de vacunación en los ejes X e Y respectivamente. El tamaño de cada burbuja representa el tamaño de la población.

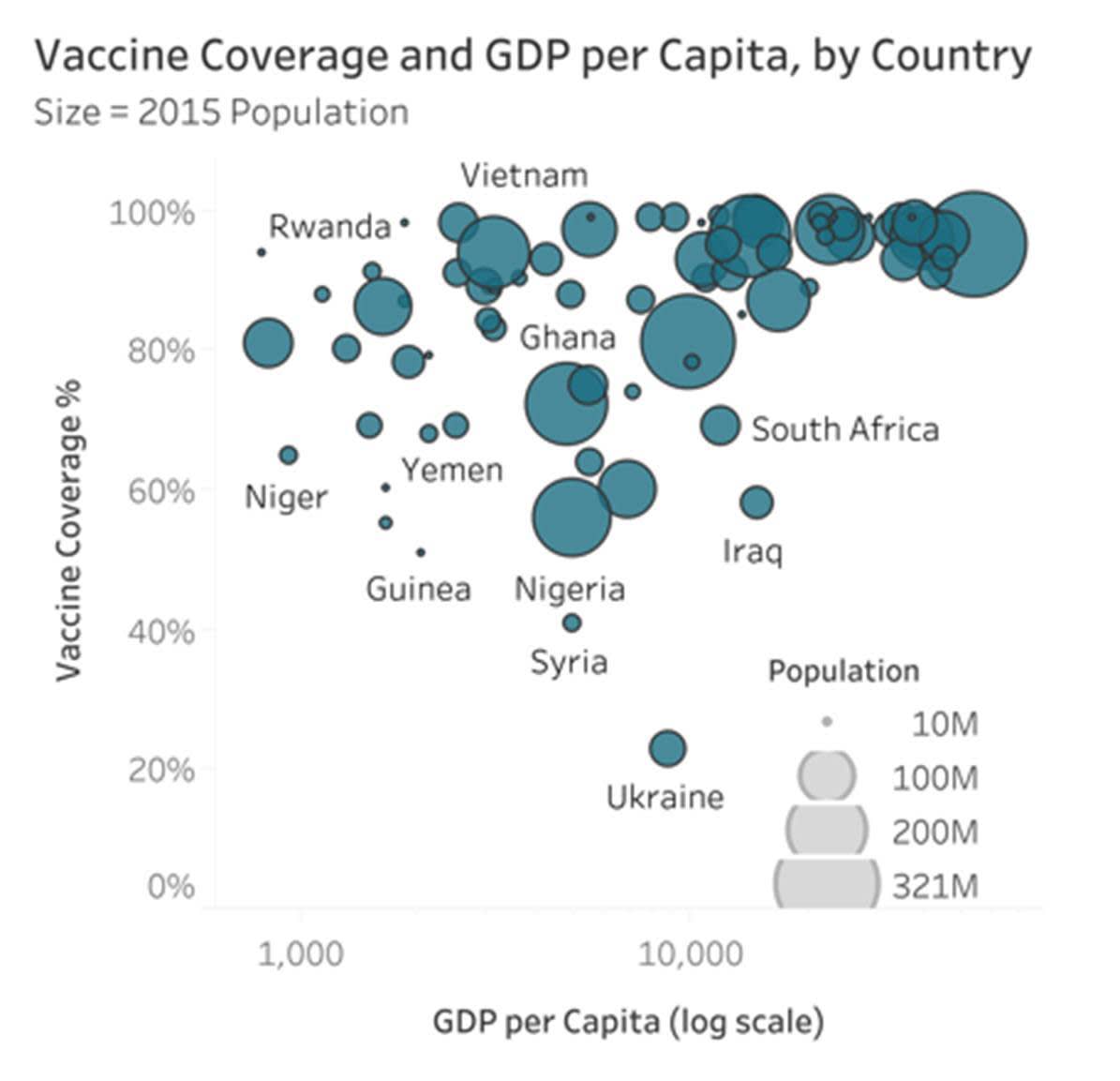
Aprendió anteriormente en este módulo que los lectores no perciben las diferencias de tamaño cuantitativo con la misma precisión que otros atributos, como la longitud. Cuando se agrega una tercera variable cuantitativa a un diagrama de dispersión, no tiene muchas otras opciones, de modo que el uso de burbujas de diferentes tamaños es un método aceptado. Al usar estas burbujas, tenga en cuenta que se pierde la precisión en la visualización de la tercera variable.

En los casos en que no hay muchos puntos de datos o solo se quiere comparar el primer y el último conjunto de valores de una de las variables, los gráficos de barras pueden venir al rescate en la forma de una lente de tabla. Las lentes de tabla admiten tres o más variables cuantitativas para compararse con una variable cualitativa (categórica) en común.

En el ejemplo, se muestran las mismas variables que en el diagrama de dispersión con burbujas de diferentes tamaños mostrado anteriormente, pero aquí solo se muestran los 10 países con la menor cobertura de vacunación. Además, la lente de tabla permite comparar muchas métricas o una sola.

Recursos

• Sitio web del Financial Times: Gráficos que funcionan: Guía de vocabulario visual de FT
• Trailhead: Distribuciones de datos
• Trailhead: Correlación y regresión
• Libro: Introducción a la estadística. Educación sobre estadística en línea: Curso de estudio multimedia interactivo, 2020 por David M. Lane.
• Entrada de blog de Sellers Dorsey: Un histograma y un polígono de frecuencia entran a un bar