Explorar la agregación
Objetivos de aprendizaje
Después de completar esta unidad, podrá:
- Definir qué es una agregación.
- Aplicar diferentes tipos de agregación.
¿Qué es la agregación?
La agregación se refiere a una recopilación de datos cuantitativos y puede mostrar tendencias de grandes volúmenes de datos. Por ejemplo, sumar todas las búsquedas web para un campamento específico o calcular los ingresos promedio de todos los asalariados en una ciudad.
En muchas herramientas de análisis, las variables cuantitativas se agregan de forma predeterminada, pero pueden desagregarse para reflejar los puntos de datos de cada valor en cada fila de la fuente de datos.
Las variables también se conocen como campos en muchas herramientas de análisis de datos.
Estas son algunas agregaciones comunes.
| Agregado | Descripción | Ejemplo: 3, 3, 6 |
|---|---|---|
|
Suma |
El total aritmético de los valores |
3 + 3 + 6 = 12 Suma = 12 |
|
Promedio |
La media aritmética de los valores (es decir, la suma dividida por el número de valores) |
3 + 3 + 6 = 12 12/3 = 4 Promedio = 4 |
|
Mediana |
El valor medio de una lista de valores ordenados de menor a mayor (o de mayor a menor) |
3, 3, 6 Valor medio = 3 |
|
Mínimo |
El valor más bajo |
3, 3, 6 Mínimo = 3 |
|
Máximo |
El valor mayor |
3, 3, 6 Máximo = 6 |
|
Conteo |
El número de valores (en una tabla de datos, el número de filas o registros) |
Existen tres valores Conteo = 3 |
|
Conteo distinto (o conteo único) |
El número de valores distintos, donde cada valor único se cuenta solamente una vez (en una tabla de datos, el número de filas únicas de registros) |
Hay dos valores únicos, 3 y 6 Conteo distinto (o conteo único) = 2 |
Ejemplos de agregación
Veamos algunos ejemplos de agregaciones y el impacto que tienen en el análisis de datos. Usaremos datos de encuesta asociados a una prueba de vocabulario en línea. Cada participante realizó un cuestionario de vocabulario en línea y luego respondió algunas preguntas demográficas sobre sí mismo.
Ver una visualización con una variable cuantitativa agregada
Consultemos la variable cuantitativa Age (Edad) en la siguiente visualización. Observe que la agregación de Sum (Suma) suma todos los valores de la variable Age (Edad) para un total de 420 085 años.
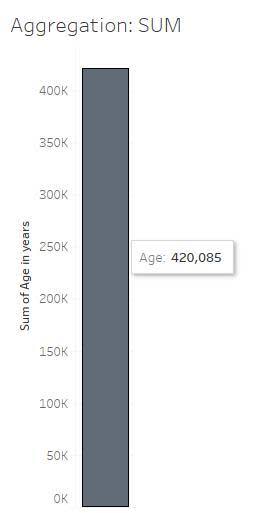
En el gráfico anterior, una sola barra resume todos los datos (12 168 filas) del conjunto de datos como un solo número.
Este valor de Sum of Age (Suma de edad) se puede desglosar por el nivel de educación más alto, lo que da como resultado una barra que muestra la edad total para cada nivel de educación. (Si suma cada uno de estos valores, es lo mismo que el total de la barra única. 116 602 + 160 542 + 120 351 + 22 092 + 498 = 420 085).
Importante: La suma no es una agregación apropiada aquí, ya que una edad de 116 602 años no es significativa. Para algunas variables, como la edad en este ejemplo, el uso de la agregación de suma no es una representación útil o adecuada de los datos. (En otros ejemplos, la suma puede ser una agregación apropiada). Al crear o visualizar visualizaciones, es importante prestar atención a las agregaciones que se utilizan en análisis y gráficos.
Ver datos subyacentes
Para comprender mejor qué valores se totalizan, veamos los datos sin procesar. Cuando examina los datos a nivel de fila, ve una fila para cada participante y su nivel de educación y edad.
Si se observa el nivel de educación Choose not to say (Elige no decir), la suma de Age (Edad) es 498.
13 + 13 + 13 + 13 + 15 + 16 + 16 + 16 + 17 + 17 + 18 + 20 + 20 + 23 + 37 + 45 + 53 + 65 + 68 = 498 años
Ver el impacto de la agregación promedio
Miremos el mismo gráfico de barras que antes, pero cambiemos la agregación a promedio. En lugar de sumar todas las edades y mostrar ese valor, ahora la altura de las barras es su promedio aritmético. Para cada nivel educativo, se suman todas las edades y se dividen por el número de valores.
Si analizamos el nivel educativo Choose not to say (Elige no decir) (se muestra en celeste), el promedio es 26,21 años.
13 + 13 + 13 + 13 + 15 + 16 + 16 + 16 + 17 + 17 + 18 + 20 + 20 + 23 + 37 + 45 + 53 + 65 + 68 = 498
498 ÷ 19 = 26,21
Ahora bien, los números son edades que parecen realistas para una persona (aproximadamente, de 20 a 43 años). Además, en promedio, los encuestados más jóvenes tienen menos educación.
Ver el impacto de la agregación de valor medio
Exploremos cuando se agrega Age (Edad) como valor medio en un conjunto de datos. Los valores extremos pueden estirar o sesgar los promedios. Por ejemplo, si una persona de 103 años realizó el cuestionario, su edad podría hacer que pareciera que su categoría educativa tenía participantes de mayor edad en general. Para evitar el problema de sesgo debido a valores extremos, la agregación de VALOR MEDIO clasifica todos los valores en orden (de mayor a menor o de menor a mayor) y devuelve el valor medio.
Para obtener más información sobre los valores medios, consulte el módulo Distribuciones de datos.
Si analizamos el nivel educativo Choose not to say (Elige no decir) (se muestra en celeste), el valor medio de la edad es de 17 años.
13, 13, 13, 13, 15, 16, 16, 16, 17, 17, 18, 20, 20, 23, 37, 45, 53, 65, 68
En este gráfico, podemos ver que las edades medias son un poco más bajas. Se podrían esperar valores medios más bajos porque no hay límite de edad para realizar el cuestionario, mientras que los participantes deben tener al menos 13 años para participar. Esto significa que no puede haber valores extremos jóvenes que hagan bajar el promedio. Además, las tendencias generales siguen apareciendo: cuanto más educación, mayores son los participantes.
Explorar el impacto de las agregaciones mínimas y máximas
La agregación mínima devuelve el valor más bajo en los datos seleccionados, mientras que la agregación máxima devuelve el valor más alto.
Si analizamos el nivel educativo Choose not to say (Elige no decir) (se muestra en celeste), la edad mínima es de 13 años.
13, 13, 13, 13, 15, 16, 16, 16, 17, 17, 18, 20, 20, 23, 37, 45, 53, 65, 68
Si analizamos el nivel educativo Choose not to say (Elige no decir) (se muestra en celeste), la edad máxima es de 68 años.
13, 13, 13, 13, 15, 16, 16, 16, 17, 17, 18, 20, 20, 23, 37, 45, 53, 65, 68
Explorar el impacto de la agregación de conteo
Ahora, exploremos qué sucede si la edad se agrega como un conteo. Un conteo devuelve el número de valores de los datos de la categoría seleccionada. Esto significa que ya no nos fijamos en la edad, sino en el número de participantes.
Si se observa el nivel de educación Choose not to say (Elige no decir), el conteo es 19 y el conteo distinto es 12. El conteo distinto es 12 porque cuatro participantes tenían 13 años, dos participantes tenían 16 y dos tenían 20 años. Contamos 12, 13 y 20 solo una vez porque la agregación distinta de conteo cuenta solo valores únicos.
| El conteo es 19 13 13 13 13 15 16 16 16 17 17 18 20 20 23 37 45 53 65 68 |
El conteo distinto es 12 13 15 16 17 18 20 23 37 45 53 65 68. |
|---|
Los conteos nos muestran que son muy pocos los participantes que se negaron a brindar su nivel educativo.
Ejemplo de desagregación
El primer gráfico que observó era una vista completamente agregada de los datos: había un valor, la suma general. Luego, el conjunto completo de datos se desglosó por nivel de educación para mostrar el desglose de la suma de edades para cada nivel educativo. En lugar de observar la suma (o el promedio o el mínimo) de todas las edades en el conjunto de datos, cada barra se agrega al nivel de cada categoría educativa. Los datos todavía están agregados, pero a un nivel más detallado.
 |
 |
Ahora, consideremos los datos originales nuevamente.
Cada fila representa un participante. Si quisiéramos ver la edad de cada participante en lugar de un valor agregado, podríamos desagregar completamente los datos o trazar cada punto en el conjunto de datos.
Explorar el impacto de los datos desagregados
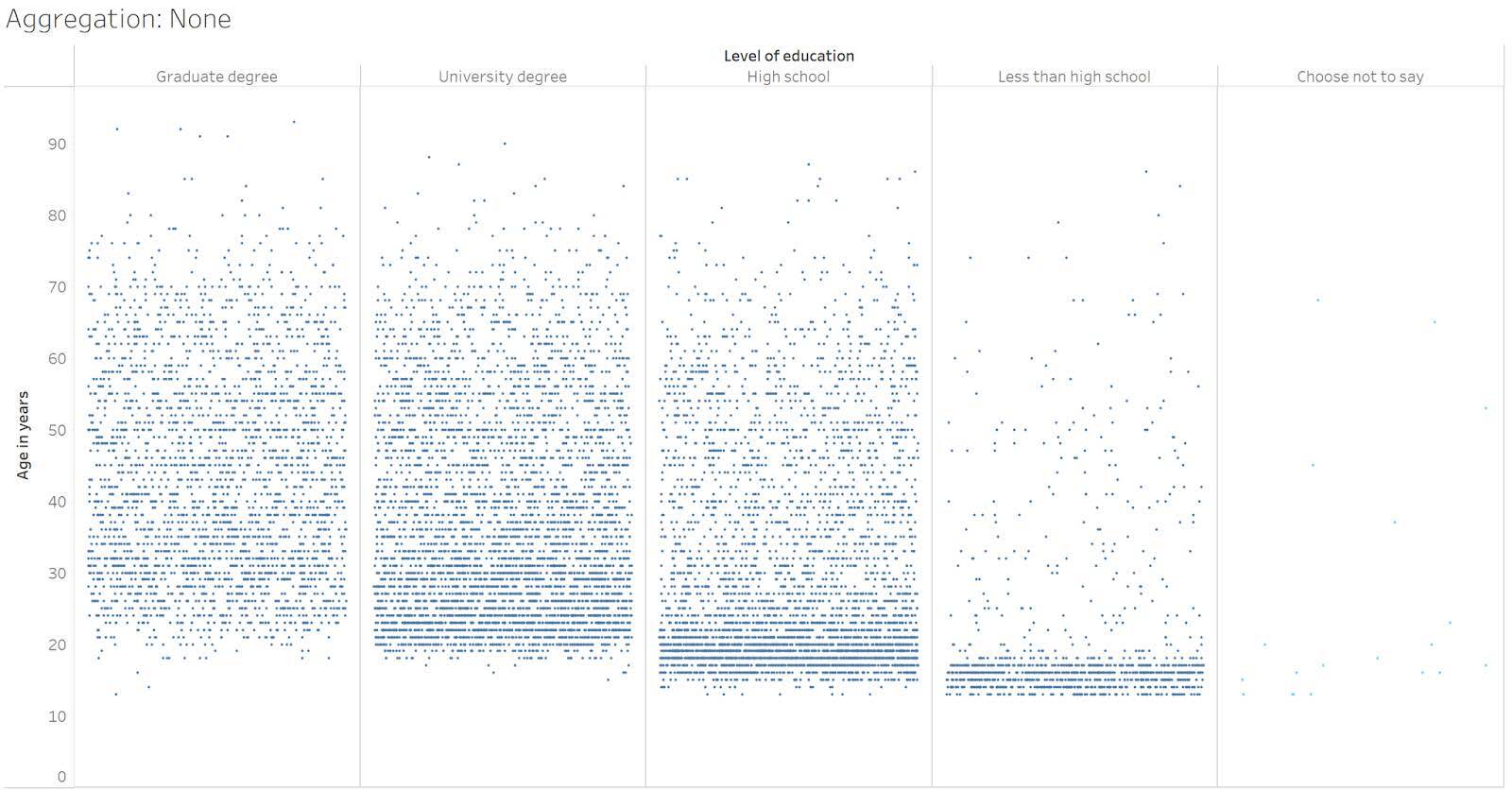
Este gráfico utiliza fluctuación para distribuir los puntos o marcas de datos. La fluctuación se refiere a colocar aleatoriamente las marcas a lo largo de un eje que no tiene intervalos (aquí, el eje x) para ayudar a revelar la densidad de los datos. Si no hubiera fluctuación, todas las calificaciones se apilarían en una única línea vertical por nivel de educación. En un gráfico de fluctuación, la ubicación horizontal de una marca es aleatoria y no transmite ningún significado particular.
En esta visualización, podemos ver que hay más participantes con edades más jóvenes y menos participantes a medida que aumentan las edades. También podemos ver que, aunque hay algunos participantes mayores en la categoría Less than high school (Secundario no completo), la mayoría de ellos son bastante jóvenes: menores de veinte años. La categoría High school (Secundario completo) tiene la mayor cantidad de edades alrededor de los 20 años, lo que podría indicar que actualmente son estudiantes universitarios. También hay muy pocos participantes con títulos de posgrado menores de 20 años. Los datos desagregados coinciden bastante bien con expectativas realistas basadas en lo que sabemos sobre la edad y el nivel de educación.
¡Pruébela!
Reto: Tiene la siguiente tabla con tres filas de datos sobre los lectores de periódicos por semana.
| Nombre | Periódicos leídos por semana |
|---|---|
|
Brooklyn |
2 |
|
Morgan |
3 |
|
Vaida |
7 |
¿Cómo se agregarían los valores de la variable Newspapers read per week (Periódicos leídos por semana) (2, 3 y 7) como suma, promedio, valor medio, mínimo, máximo y conteo? Tómese un momento para pensar en ello y luego verifique sus respuestas usando las tarjetas interactivas que se muestran a continuación.
Lea el tipo de agregación en cada tarja, piense cuál sería el valor para esa agregación y, luego, haga clic en la tarjeta para ver la respuesta correcta. Haga clic en la flecha hacia la derecha para pasar a la tarjeta siguiente y en la flecha hacia la izquierda para regresar a la tarjeta anterior.
Exploró el modo en que las agregaciones inciden en los datos y el efecto de desagregar los datos. En la siguiente unidad, profundizará en estos conceptos y aprenderá sobre granularidad.