Durchführen von Abweichungs-, Verteilungs- und Korrelationsvergleichen

Lernziele

Nachdem Sie diese Lektion abgeschlossen haben, sind Sie in der Lage, die folgenden Aufgaben auszuführen:

Beschreiben von Abweichungs-, Verteilungs- und Korrelationsvergleichen
Erläutern der bewährten Vorgehensweisen für das Anstellen von Vergleichen mit Diagrammen

Abweichung

Bei Abweichungsvergleichen geht es darum, wie stark die Werte von einem Basiswert oder manchmal auch einem Durchschnitts- bzw. Schwellenwert abweichen.

Divergierende Balkendiagramme

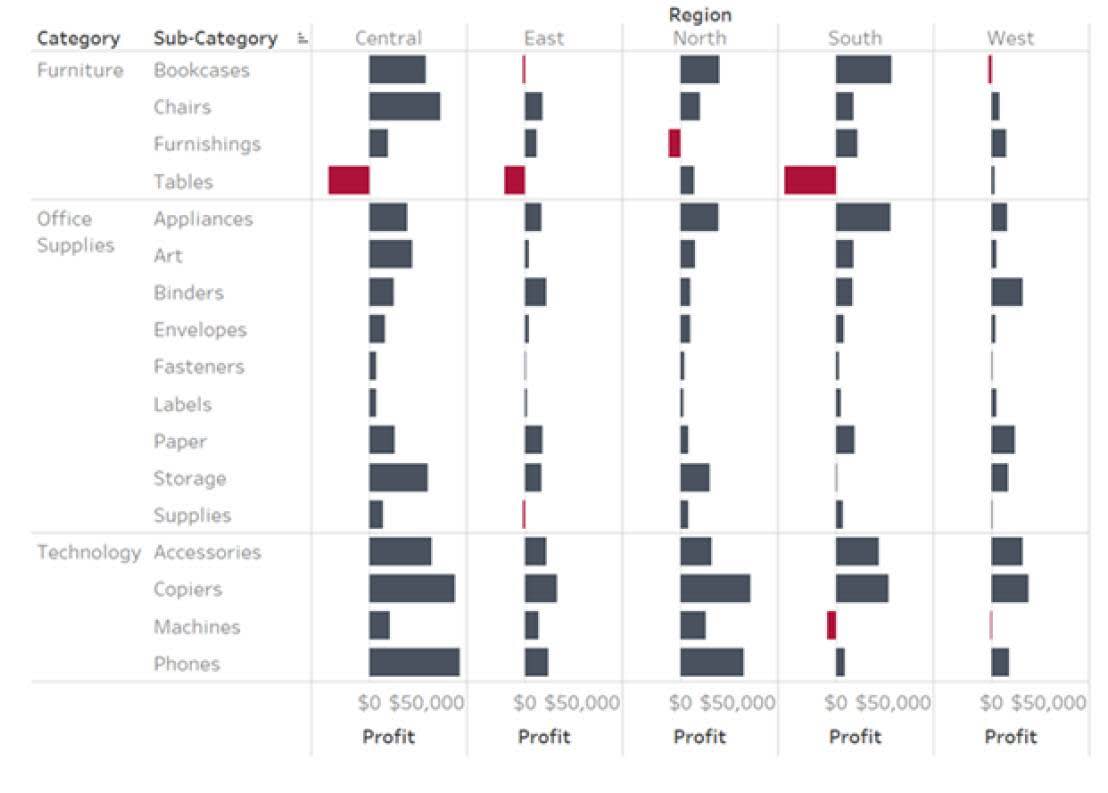
Im folgenden Beispiel zeigt die Länge der Balken den Abstand von einem Bezugswert von Null, um die Höhe des Gewinns oder Verlusts anzuzeigen. Sie können schnell erkennen, welche Artikel und Regionen nicht rentabel sind.

Divergierendes Balkendiagramm, das die Gewinne und Verluste für Produktkategorien und Regionen zeigt

Liniendiagramme

Sie haben bereits gelernt, dass Liniendiagramme mit am besten geeignet sind, um die Veränderung von Werten im Zeitverlauf darzustellen. Auch für die Darstellung von Abweichungen im Zeitverlauf ist ein Liniendiagramm eine gute Möglichkeit. Im nächsten Beispiel wird für jeden Monat die prozentuale Veränderung des Patientenvolumens in der Notaufnahme zwischen 2015 und 2016 gegenüber dem Vorjahr dargestellt. Sie können sehen, dass der Juni den größten Anstieg des Patientenvolumens im Vergleich zum Vorjahr aufweist.

Liniendiagramm, das für jeden Monat die prozentuale Änderung gegenüber dem Vorjahr zeigt.

Verteilungen

Eine Verteilung zeigt alle möglichen Datenwerte und die Häufigkeit (Anzahl) ihres Vorkommens. Mit anderen Worten: Eine Verteilung beschreibt, wie oft jeder Datenwert in einem Datenset vorkommt.

Histogramme

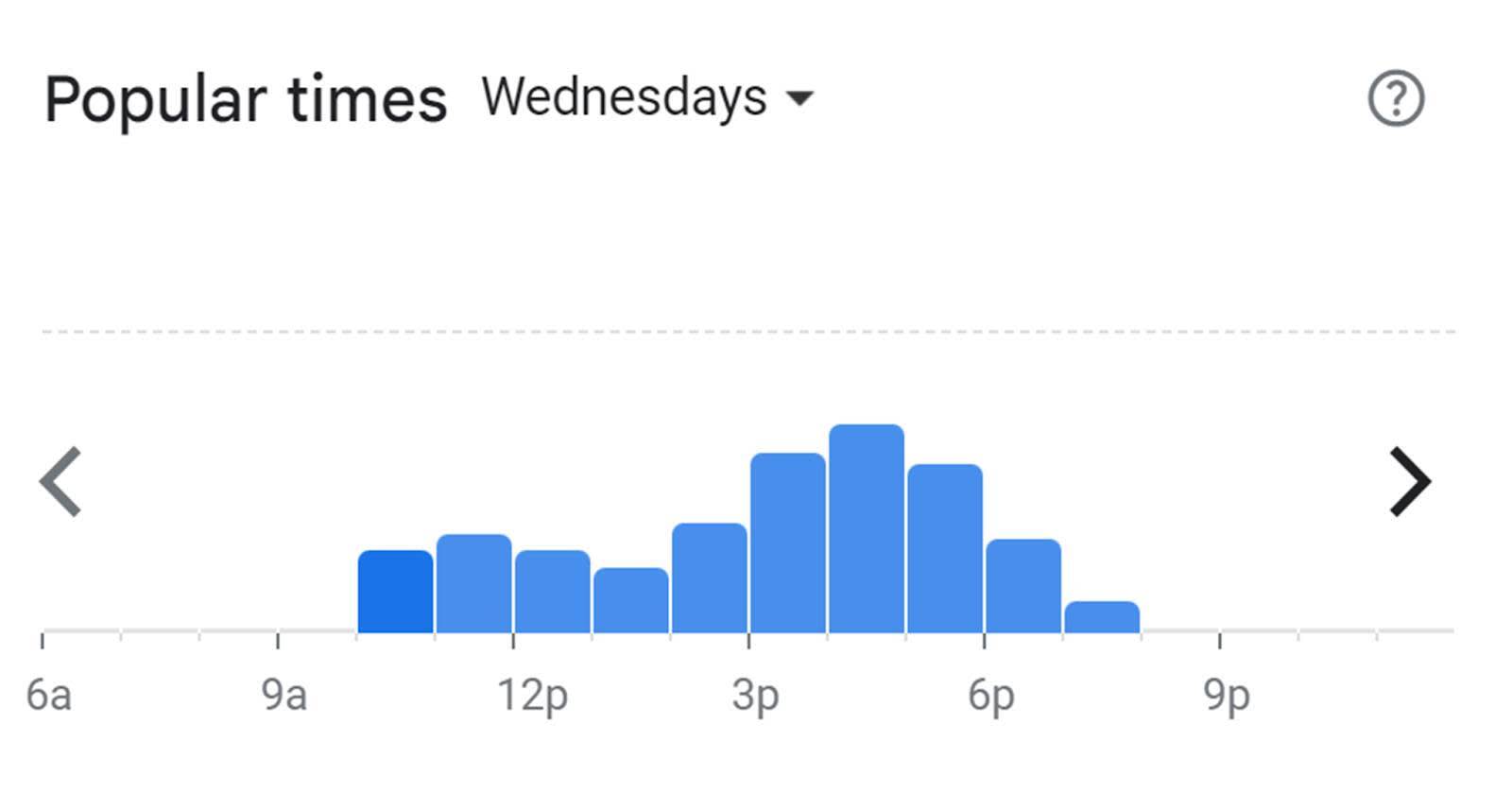
Haben Sie schon einmal eine Navigations-App auf dem Smartphone benutzt, um die Stoßzeiten in Ihrem Lieblingsrestaurant zu ermitteln? Vielleicht ist Ihnen die Grafik aufgefallen, die Ihnen die Stoßzeiten anzeigt. Diese Grafik ist ein Histogramm. Der Spitzenwert zeigt die Zeit mit der höchsten Auslastung an.

Histogramm aus Google Maps, das Stoßzeiten für ein Restaurant zeigt.

Ein Histogramm ist ähnlich wie ein Balkendiagramm, gruppiert aber quantitative Werte in gleich große Bereiche (Klassen) und zählt für die Histogrammanzeige, wie viele Werte sich in jeder Klasse befinden. Bei der Verwendung von Programmen wie Tableau bestimmt das Programm automatisch die Klassengröße und gibt die Häufigkeit (oder Anzahl) der Werte in jeder Klasse an.

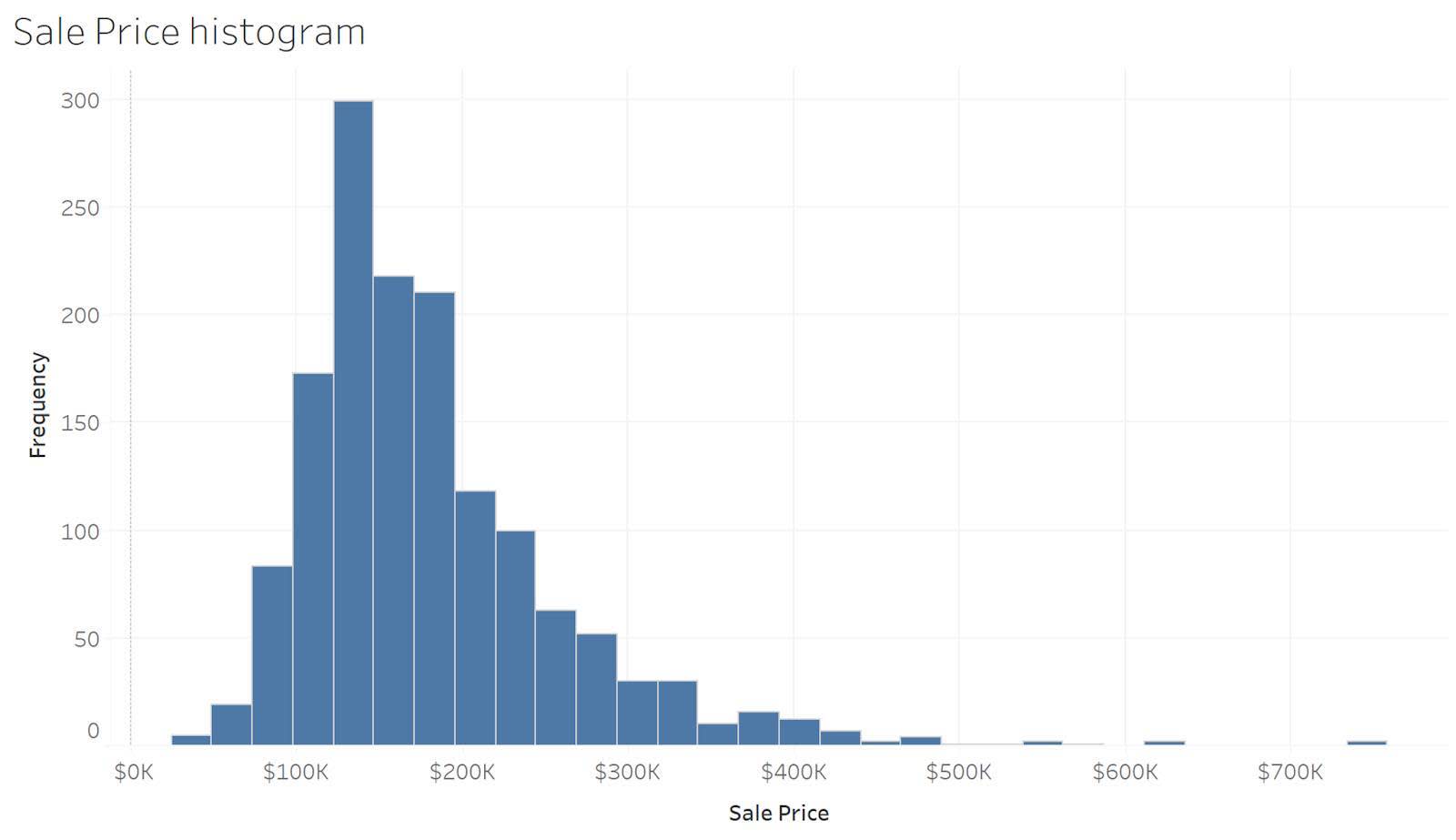
Im folgenden Beispiel gibt das Histogramm einen detaillierten Überblick über die Immobilienpreise für das gesamte Datenset. Wie Sie sehen, liegt der Verkaufspreis der meisten Immobilien zwischen 100.000 und 200.000 US-Dollar. Das Histogramm zeigt auch, dass es im Vergleich zur Mehrheit der Immobilien einige wenige höherpreisige Objekte gibt.

Histogramm mit Immobilienpreisen

Verteilungen können manchmal auch als Prozentsätze anstelle von Anzahlen oder Häufigkeiten dargestellt werden.

Häufigkeitspolygone

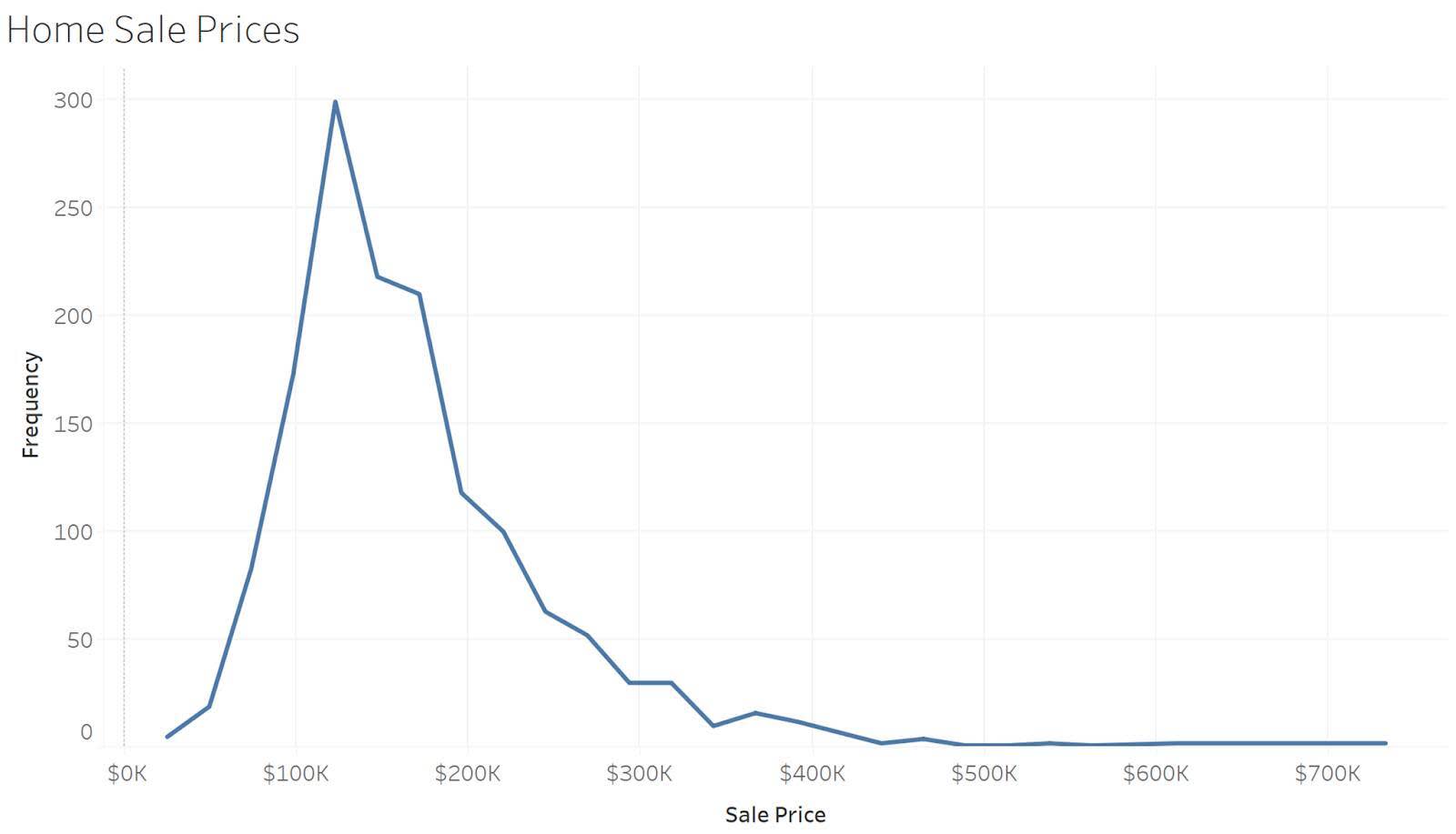
Häufigkeitspolygone sind ähnlich wie Histogramme, mit dem Unterschied, dass sie Linien verwenden, um die Häufigkeitswerte zu verbinden. Das folgende Beispiel zeigt dieselben Daten wie das obige Histogramm, allerdings werden hier die Anzahlen in jeder Klasse mit einer Linie verbunden. Die Linie macht die Darstellung für den Betrachter klarer und einfacher.

Häufigkeitspolygon, das die Verteilung von Immobilienpreisen zeigt

Verwenden Sie Häufigkeitspolygone anstelle von Histogrammen, wenn Sie mehr als eine Verteilung im selben Diagramm darstellen möchten.

Streifendiagramme

Streifendiagramme zeigen einen Punkt für jeden Datenwert in einer Linie und brauchen viel weniger Platz als Histogramme oder Häufigkeitspolygone. Streifendiagramme können ein effizientes Mittel sein, um den Bereich einer Verteilung darzustellen und zu zeigen, ob es Wertehaufen gibt. Wenn mehrere Werte gleich sind oder sehr nahe beieinander liegen, werden sie übereinander eingezeichnet. Dies macht es schwierig, Werte zu unterscheiden, die in den Daten häufig vorkommen.

Im folgenden Beispiel, für das dieselben Daten wie im Histogramm verwendet werden, wird deutlich, dass Sie mit dem Streifendiagramm zwar die einzelnen höherpreisigen Immobilien leicht erkennen können, dass es aber schwierig ist, die häufigsten Verkaufspreise zu erkennen. Es empfiehlt sich daher, Streifendiagramme bei kleineren Datensets zu verwenden.

Streifendiagramm, das die Verteilung von Immobilienpreisen zeigt

Wenn Sie die Punkte in einem Streifendiagramm transparent machen, erscheinen mehrere übereinanderliegende Punkte dunkler und der Betrachter kann zwischen einzelnen Werten und mehreren ähnlichen Werten unterscheiden.

Boxplots

Boxplots zeigen Verteilungen in kompakterer Form als Histogramme. Und beim Vergleich mehrerer Verteilungen bieten Boxplots eine effiziente Möglichkeit, Verteilungen zwischen Kategorien zu vergleichen. Die Box in einem Boxplot zeigt die mittleren 50 % bzw. das 25. bis 75. Perzentil der Daten und enthält eine Linie, die den Medianwert oder das 50. Perzentil zeigt.

Aber was ist mit den Daten, die nicht in diese Kategorie fallen? Hier kommen die sogenannten Whiskers ins Spiel. Außerhalb der Box gezeichnet, sind Whiskers vertikale Linien, die in einem horizontalen Strich enden. Sie geben Aufschluss über Werte, die nicht in den mittleren 50 % der Daten (der Box) liegen, und legen eine Grenze zur Unterscheidung von Ausreißern fest. Ausreißer können als atypische und seltene Beobachtungen oder Werte verstanden werden, die eine extreme Abweichung vom Zentrum einer Verteilung aufweisen.

Bei Boxplots gibt es verschiedene Möglichkeiten, die Grenze für potenzielle Ausreißer zu berechnen. Einige Programme kennzeichnen extreme Ausreißer mit einem anderen Symbol, wenn diese Werte weiter entfernt sind als die typische Grenze.

Im nächsten Beispiel werden die Verteilungen der Immobilienpreise für verschiedene Gebäudetypen verglichen. Sie können sehen, dass Einfamilienhäuser einen viel größeren Wertebereich umfassen als alle anderen Gebäudetypen, einschließlich vieler höherpreisiger Häuser, die Ausreißer zu sein scheinen.

Boxplots zum Vergleich der Verkaufspreisverteilungen verschiedener Immobilientypen

Dieses Boxplot-Beispiel enthält zudem vertikale Streifendiagramme zur Darstellung jedes einzelnen Werts. Sie können nun jeden Datenpunkt und Details über die Verteilung in der gleichen Visualisierung betrachten. Man braucht vielleicht etwas Übung, bis bis man Boxplots richtig liest, aber sie können viele Informationen über eine Verteilung vermitteln, ohne viel Platz zu beanspruchen.

Sehen Sie sich das Modul "Datenverteilungen" in Trailhead an, um mehr über Verteilungen zu erfahren.

Korrelationen

Bei Korrelationsvergleichen werden die Beziehungen zwischen quantitativen Variablen betrachtet. Sie liefern Antworten auf Fragen wie "Steigt oder fällt der Wert einer Variablen zusammen mit einer anderen Variablen?"

In der Statistik kann der Begriff Korrelation bestimmte Bedeutungen haben. Wenn zum Beispiel von Korrelationskoeffizienten die Rede ist, bezieht sich dies auf eine bestimmte Art von Beziehung zwischen quantitativen Variablen, die in der Regel linear ist. Im Modul Korrelation und Regression erfahren Sie mehr darüber, wie Sie Korrelations- und Regressionsanalysen durchführen.

Streudiagramme

Streudiagramme werden verwendet, um die Beziehung zwischen zwei quantitativen Variablen aufzuzeigen, wobei eine Variable auf der X-Achse und die andere auf der Y-Achse aufgetragen wird. Streudiagramme können zeigen, ob es eine Beziehung zwischen den Variablen gibt. Beispiele: "Bewegt" sich eine Variable in die gleiche Richtung wie die andere und, welche Art von Beziehung liegt vor, beispielsweise ein linearer Zusammenhang oder ein anderes Muster.

Anhand von Streudiagrammen lassen sich auch Ausreißer erkennen. Das folgende Beispiel zeigt die Beziehung zwischen dem Immobilienpreis und der Wohnfläche. Jeder Punkt im Streudiagramm stellt eine einzelne, in das Diagramm eingeflossene Immobilie dar, wobei der Immobilienpreis auf der Y-Achse und die Wohnfläche auf der X-Achse aufgetragen wird.

Streudiagramm, das den Immobilienpreis bezogen auf die Wohnfläche zeigt

Ein Streudiagramm kann zwar eine Beziehung zwischen zwei Variablen aufzeigen, es beweist jedoch nicht, dass sich eine Variable auf die andere auswirkt. Vielleicht haben Sie schon einmal den Satz gehört: "Korrelation ist nicht gleich Kausalität". Es kann viele Gründe für die Beziehung zwischen den Variablen geben.

Trendlinien

Trendlinien in Streudiagrammen helfen Ihnen, das Gesamtmuster der Beziehung zu erkennen und die Gesamtform der Daten zusammenzufassen. In unserem Beispiel zu Immobilienpreis und Wohnfläche hilft Ihnen eine lineare Trendlinie, das Gesamtmuster der Beziehung zu sehen.

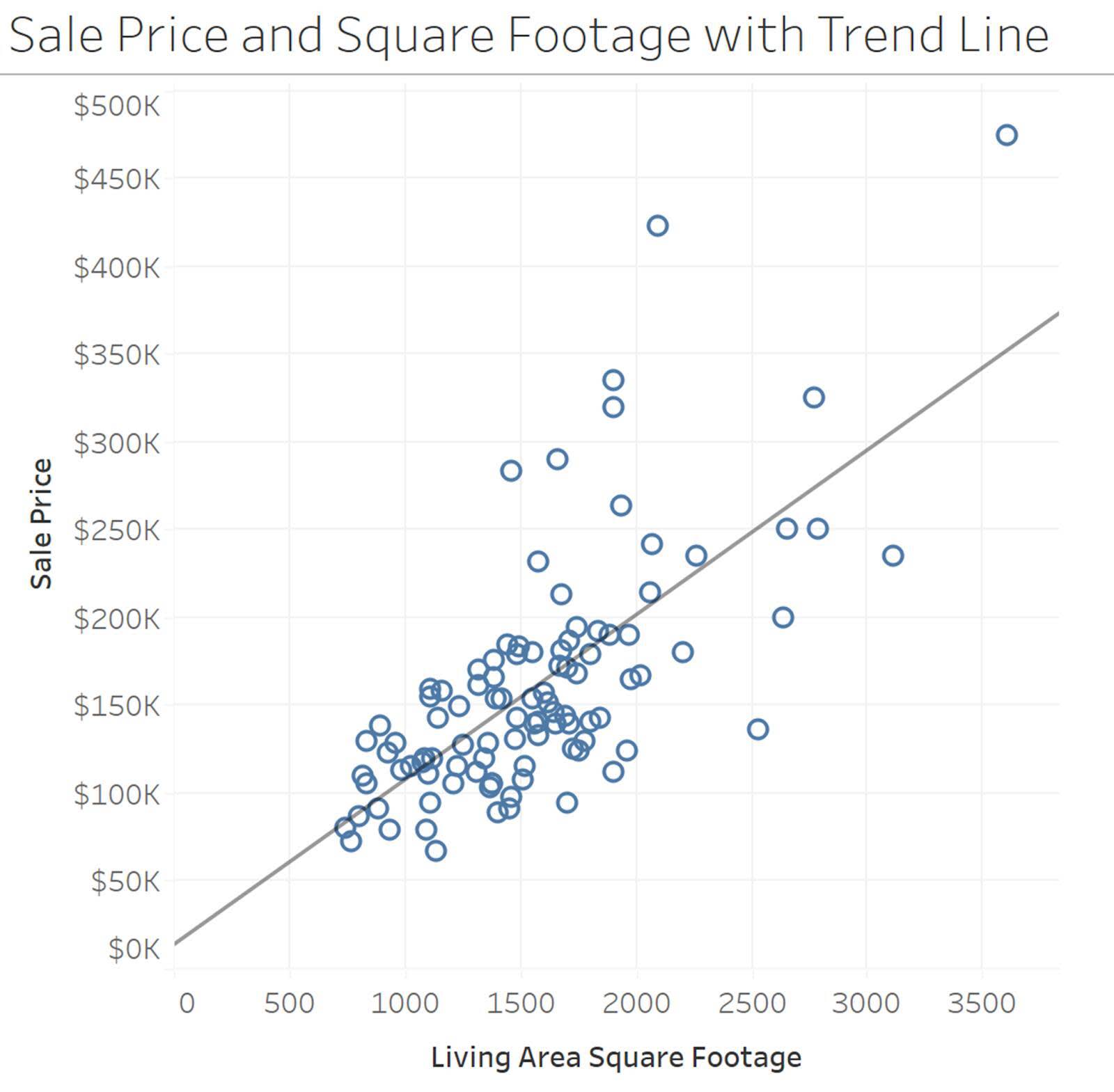
Streudiagramm mit Trendlinie, das die Beziehung zwischen Immobilienpreis und Wohnfläche zeigt

Nicht alle Beziehungen sind linear. Wenn die Form der Beziehung gekrümmt ist, können statt linearer Trendlinien auch Exponential- oder Logarithmuslinien verwendet werden.

Weitere Informationen über die Korrelation und das Erstellen einer linearen Regressionslinie finden Sie im Modul Korrelation und Regression in Trailhead.

Streudiagramme mit Blasengröße und Tabellenlinse

Die zuvor beschriebenen Streudiagramme zeigten die Beziehung zwischen zwei quantitativen Variablen, wobei eine Variable auf der X-Achse und die andere auf der Y-Achse aufgetragen wurde. Doch was tun Sie, wenn Sie mehr als zwei quantitative Variablen vergleichen möchten? Sie können ein weiteres Merkmal, die Größe, verwenden, um eine dritte Variable zu einem Streudiagramm hinzuzufügen.

Im folgenden Beispiel werden das Bruttoinlandsprodukt pro Kopf ("GDP per Capita") und die Durchimpfungsrate ("Vaccine Coverage") auf der X- bzw. Y-Achse dargestellt, und die Größe der einzelnen Blasen steht für die Bevölkerungszahl.

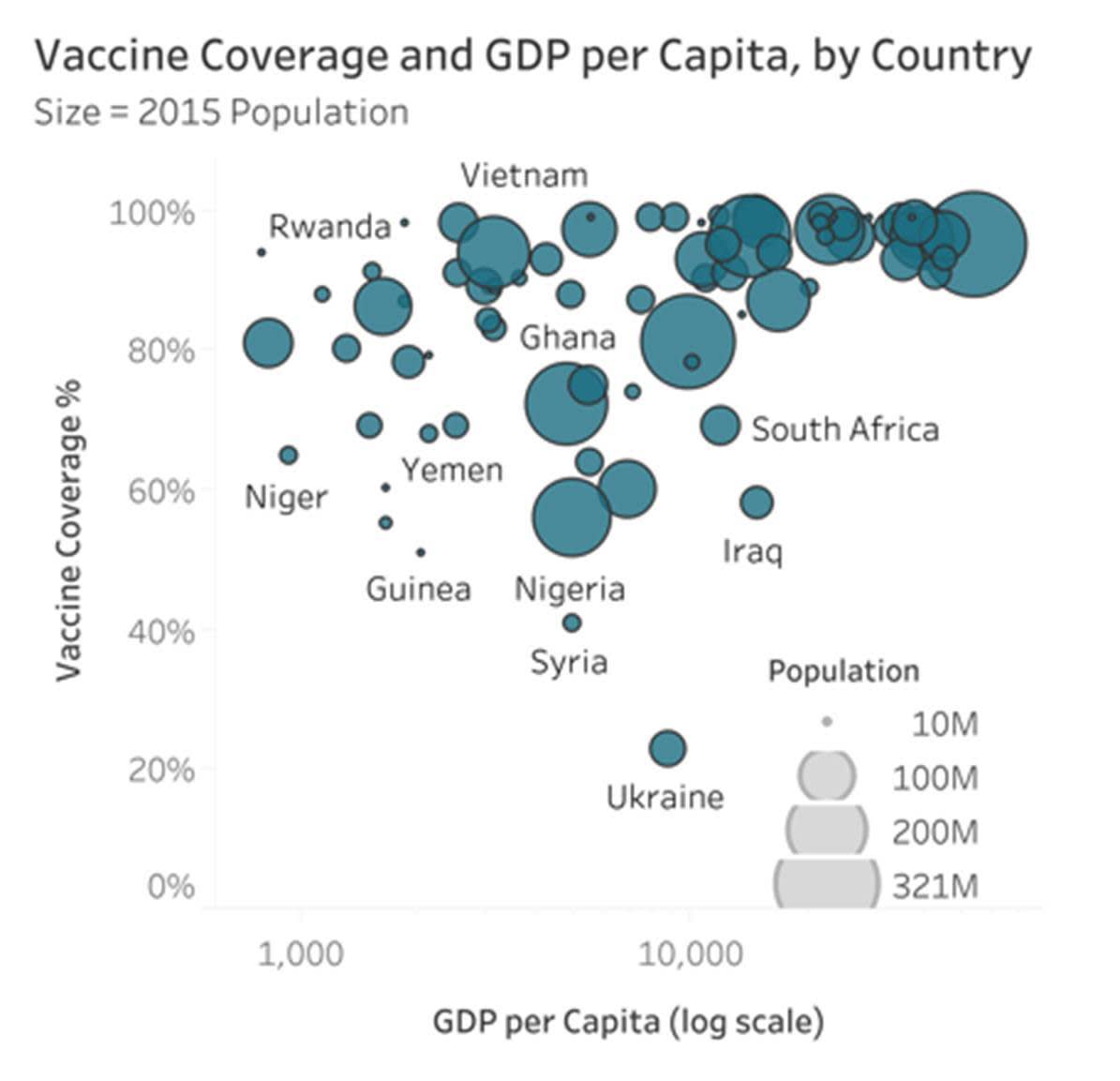
Streudiagramm mit Blasengröße, das die Durchimpfungsrate ("Vaccine Coverage") in Prozent, das Bruttoinlandsprodukt pro Kopf ("GDP per Capita") und die Bevölkerungszahl nach Land zeigt

Wie Sie bereits an früherer Stelle in diesem Modul gelernt haben, nehmen Betrachter quantitative Größenunterschiede nicht so präzise wahr wie andere Merkmale, z. B. die Länge. Beim Hinzufügen einer dritten quantitativen Variable zu einem Streudiagramm haben Sie nicht viele andere Möglichkeiten, und daher ist die Verwendung der Blasengröße in Streudiagrammen eine akzeptierte Methode. Bei der Verwendung der Blasengröße sollten Sie sich der Tatsache bewusst sein, dass die dritte Variable mit eingeschränkter Genauigkeit wahrgenommen wird.

Wenn es nicht viele Datenpunkte gibt oder Sie nur die oberste oder unterste Wertemenge einer der Variablen vergleichen möchten, können Balkendiagramme in Form einer Tabellenlinse hier eine Lösung darstellen. Mit der Tabellenlinse können drei oder mehr quantitative Variablen mit einer gemeinsamen qualitativen (kategorialen) Variable verglichen werden.

Das Beispiel zeigt dieselben Variablen wie das oben gezeigte Streudiagramm mit Blasengröße, mit dem Unterschied, dass hier nur die zehn Länder mit der niedrigsten Durchimpfungsrate gezeigt werden. Mit der Tabellenlinse können Sie auch Vergleiche zwischen mehreren Kennzahlen oder innerhalb einer einzelnen Kennzahl anstellen.

Tabellenlinse, die die Durchimpfungsrate ("Vaccine Coverage") in Prozent, das Bruttoinlandsprodukt pro Kopf ("GDP per Capita") und die Bevölkerungszahl nach Land zeigt

Benötigen Sie Hilfe?

Mehr entdecken