Make Deviation, Distribution, and Correlative Comparisons

Learning Objectives

After completing this unit, you’ll be able to:

Describe deviation, distribution, and correlative comparisons.
Understand the best practices for making comparisons with charts.

Deviation

Deviation comparisons focus on the amount that values differ from a baseline value, sometimes an average or threshold value.

Diverging Bar Charts

In the example, the length of bars are showing the distance from a center value of zero to show the amount of profit or loss. You can quickly see which items and regions are not profitable.

Diverging Bar Chart showing profits and losses for Product categories and regions.

Line Charts

Earlier, you learned how line charts are one of the best ways to show a change in values over time. Similarly, when you want to show deviation over time, a line chart is a good option. In the next example, the year-over-year ER patient volume percent change between 2022 and 2023 for each month is shown. You can see that June had the greatest increase in patient volume from the year before.

Line graph showing year-over-year percent change from 2022 to 2023 for each month.

Distributions

A distribution shows all the possible data values and the frequency (count) of their occurrence. In other words, a distribution describes how many times each data value occurs in a set of data.

Histograms

Have you used a mapping app on your phone to discover busy times at your favorite restaurant? You may have noticed the graph that shows you the busy times. This graph is a histogram. The peak shows the most busy time.

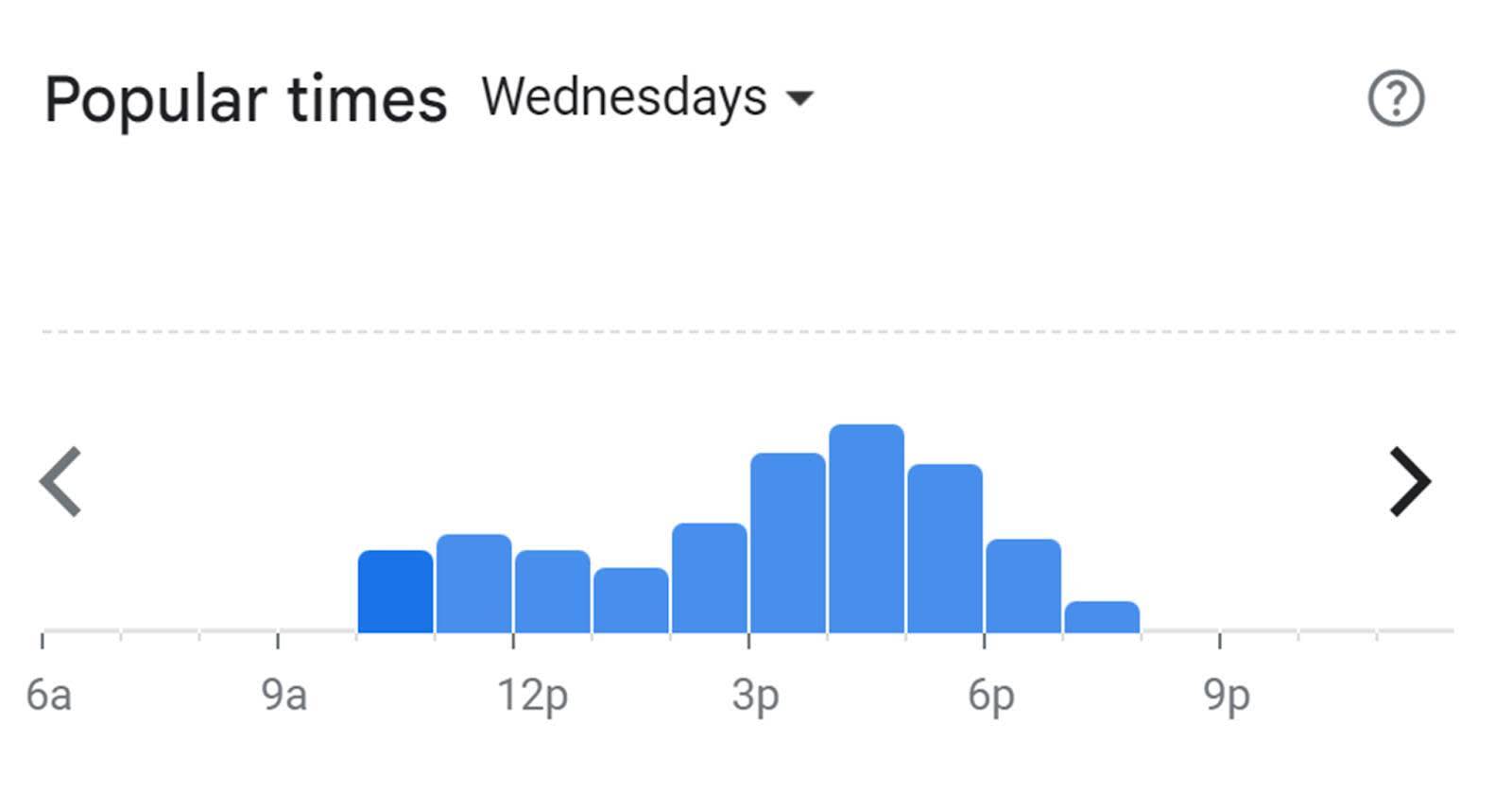
Histogram from Google Maps showing when a restaurant is most busy.

A histogram is similar to a bar chart, but it groups quantitative values into equal-sized ranges, or bins, and counts how many values are in each bin to make the histogram display. When using programs such as Tableau, the program automatically determines the bin size and gives the frequency (or count) of values in each bin.

In the following example, the histogram gives a detailed view of the home sales price values for the entire data set. You can see that most homes are selling between $100K and $200K. The histogram also shows that there are a few higher priced homes compared with the majority of homes.

Histogram of home sales prices.

Distributions can sometimes be presented as percentages instead of counts or frequencies.

Frequency Polygons

Frequency polygons are similar to histograms, except they use lines to connect the frequency counts. The following example shows the same same data as the histogram above, except the counts in each bin are connected with a line. The line provides a cleaner and simpler look for the viewer.

Frequency Polygon showing the distribution of home sale prices.

Use frequency polygons instead of histograms when you want to show more than one distribution on the same graph.

Strip Plots

Strip plots show a dot for each data value in a line and take up much less space than histograms or frequency polygons. Strip plots can be an efficient way to show the range of a distribution and if there is any clustering of values. If multiple values are the same, or very near each other, they are plotted on top of each other, making it difficult to distinguish values that occur frequently in the data.

In the following example, which uses the same data as the histogram, you can see that while the strip plot allows you to easily see the singleton higher priced homes, it’s difficult to view the most frequent sales prices. Therefore, it’s best to use strip plots when you have smaller datasets.

Strip plot showing the distribution of home sale prices.

Making the dots in a strip plot transparent can allow for multiple dots to appear darker and enables the viewer to distinguish between single values and multiple similar values.

Box Plots

Box plots display distributions in a more compact form than a histogram. And when comparing multiple distributions, box plots provide an efficient way to compare distributions between categories. The box in a box plot shows the middle 50% of data, or the 25th–75th percentile, and includes a line that shows the median, or 50th percentile, value.

But what about the data that falls outside of that? That’s where whiskers come in. Plotted outside the box, whiskers are vertical lines that end in a horizontal stroke. They provide insight about values that are not within that middle 50% of the data (the box), and give a boundary to distinguish outliers. Outliers can be understood as atypical and infrequent observations, or as values that have an extreme deviation from the center of a distribution.

In box plots, there are different ways to calculate the boundary where potential outliers should be. You may find some programs denote extreme outliers with a different symbol if those values are farther out than the typical boundary.

The next example compares the distributions of home sale prices for different building types. You can see that single family homes have a much larger range of values than any of the other building types, including many higher priced homes that appear to be outliers.

Boxplots comparing the sale price distributions of different types of homes.

This box plot example also includes vertical strip plots to show each individual value. You can now view every data point and details about the distribution in the same visual. While it may require a bit of time to learn how to read box plots, they can convey a lot of information about a distribution without using a lot of space.

Check out Data Distributions Module on Trailhead to learn more about distributions.

Correlations

Correlative comparisons explore the relationships between quantitative variables. They answer questions such as, “Does one variable increase or decrease with another variable?”

In statistics, the term correlation can have specific meanings. For example, when discussing correlation coefficients, that refers to a specific type of relationship between quantitative variables, usually linear. In the Correlation and Regression module, you learn how to perform correlation and regression analyses.

Scatter Plots

Scatter plots are used to show the relationship between two quantitative variables with one variable displayed on the x-axis and the other on the y-axis. Scatter plots can show if there is a relationship between the variables. For example, does one variable “go in the same direction” as the other, and what type of relationship is present, such as linear or different pattern.

Viewing scatter plots can also help you see outliers. The following example shows the relationship between home sale price and living square footage. Each point in the scatter plot represents a single home placed in the graph using home sale price on the y-axis and square footage on the x-axis.

Scatter plot showing Home Sale Price vs Living Area Square Footage.

While a scatter plot may show a relationship between two variables, it doesn't prove that one variable is affecting the other. You may have heard the saying, “Correlation does not prove causation.” There can be many reasons for the relationship between the variables.

Trend Lines

Trend lines in scatter plots help you see the overall pattern of the relationship and summarize the overall shape of the data. In our example of home sale price and square footage, a linear trend line helps you see the overall pattern of the relationship.

Scatter plot with trend line showing relationship between Home Sale Price and Living Area Square Footage.

Not all relationships are linear. When the shape of the relationship is curved, trend lines such as exponential or logarithmic can be used instead of linear.

Check out the Correlation and Regression module on Trailhead to learn more about correlation and creating a linear regression line.

Sized Bubble Scatter Plots and Table Lens

The previous scatter plots showed the relationship between two quantitative variables displaying one on the x-axis and the other variable on the y-axis. But what do you do when you want to compare more than two quantitative variables? You can use another attribute, size, to add a third variable to a scatter plot.

In the next example from HealthDataViz, GDP per capita and vaccine coverage are shown on the x- and y-axes respectively with the size of each bubble representing population size.

Sized bubble scatter plot showing Vaccine Coverage (%), GDP per Capita, and Population by country.

You learned earlier in this module how viewers don’t perceive quantitative size differences as accurately as other attributes such as length. When adding a third quantitative variable to a scatter plot, you don’t have many other options, so using sized bubbles in scatter plots is an accepted method. When using sized bubbles, be aware of the loss of viewing accuracy with the third variable.

In situations where there are not many data points or you only want to compare the top or bottom set of values of one of the variables, bar charts can come to the rescue in the form of a Table Lens. Table Lens allows three or more quantitative variables to be compared across a common qualitative (categorical) variable.

The example shows the same variables as the sized bubble scatter plot shown above except it only shows the 10 countries with the lowest vaccine coverage. The Table Lens also lets you compare across multiple metrics or within an individual metric.

Table Lens showing Vaccine Coverage (%), GDP per Capita, and Population by country.

Looking for Help?

Discover More