考察数据内部的相关性

学习目标

完成本单元后，您将能够：

数据素养是轻松使用和与数据通信的基础。

Data Literacy Basics（数据素养基础）模块把定量变量描述为可以用数字衡量的特征，比如每天花在看电视上的小时数、以每小时英里数为单位的速度、某个城市的年降雨总量（英寸）、美元销售额，以及花在市场营销上的费用。

考察数据内部的关系时，您如何确定两个变量，比如销售额和营销费用的相关性有多强？您可以用一个变量来预测另一个吗？

相关性和回归是用于发现趋势和进行预测的重要技术。虽然分析中使用了其他重要形式，但我们专注于人工智能和分析中使用的最简单的形式—线性相关和回归。

在本单元中，您将熟悉相关性这个概念，它描述两个变量是否彼此相关，以及相关性的密切程度。您可以了解相关性如何衡量相互关系但是并不证明因果关系。下一单元中，您将发现除了衡量这个模型与您的数据的匹配程度之外，可以如何利用线性回归根据一个变量的值来计算或预测另一个变量的值。

相关性是可以显示成对的定量变量是否相关以及相关性的强度的方法。

本单元讨论皮尔逊相关性。还有其他一些非线性相关性，这里不进行讨论。

比如，每日消耗的热量与体重是否有关系？消耗更多热量的人是否更重？相关性可以告诉您人的体重与他们的热量摄入相关程度。

体重和热量摄入之间的相关性只是一个简单的例子，但是有时候您需要处理的数据未必具有您预期的关系。还有一些时候，您可能怀疑存在相关性，但是不知道哪个是最强的。相关性分析有助于您了解您的数据。

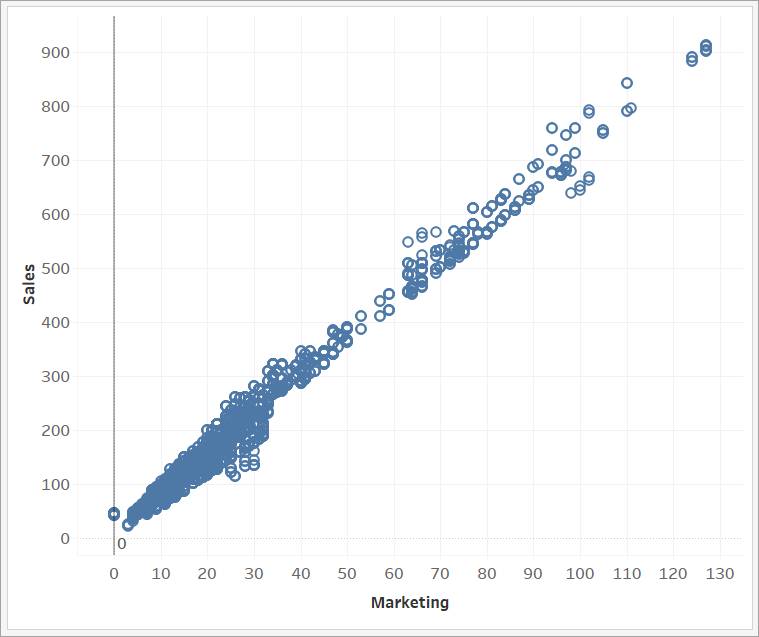
开始相关性分析时，您可以创建一张散点图来考察两个定量变量之间的关系。变量绘制为笛卡尔坐标，标记每个数据点在水平 x 轴上的距离和垂直 y 轴上的距离。在下面的散点图中，您可以看出销售额和营销费用之间的关系。似乎存在相关性：随着一个变量升高，另一个似乎也升高。

提示两个定量变量之间的相关性的散点图

本单元中的概念从 David M. Lane 的网络公开著作《统计学入门》改编而来。

皮尔逊相关性，也叫相关性系数，用来衡量两个定量变量间的线性关系的强度和方向（正相关或负相关）。衡量数据样本中的相关性时，所用的符号是字母 r。皮尔逊的 r 介于 -1 到 1 之间。

当 r = 1 时，两个变量之间存在完美的正线性关系，意思是随着数值提高，两个变量完美相关。当 r = -1 时，变量之间存在完美的负线性关系。在完美的负相关性中，当一个变量增加时，另一个变量以相同的幅度减小。当 r = 0 时，表示两个变量间不存在线性关系。

对于实际数据，r 的值不可能是 -1、0 或 1。

通常 r 越接近 1 或 -1，相关性越强，如下表所示。

关于这个主题的有些资源把相关性简单地划分为强、中等或弱。

为了保证相关性有意义，您需要考虑一些条件：必须使用定量变量描述线性关系，同时考虑所有异常值的影响。在进行相关性分析之前，您应该检查这些条件。

1973 年，一位名叫 Francis Anscombe 的统计学家开发出了“安斯库姆四重奏”，可以图形化展示图表数据的重要性，与简单地运行统计学测试不同。他的四重奏中的四个可视化都显示了相同的趋势线方程。四张图说明为什么可视化如此重要，它们可以帮助我们发现数据内部可能被统计学测试掩盖的趋势。

在下面的例子中，四张图中只有左上角的散点图满足线性且没有异常值的条件。右上角的散点图未显示线性关系，非线性模型会更合适。底部的两个散点图都有异常值，这些异常值会极大地影响结果。

四张散点图，突出显示左上角的散点图，显示线性关系且没有异常值

既然您已经熟悉围绕相关性统计方法的概念，那么您已经准备好进入下一个单元，学习线性回归。