通过线性回归发现关系
学习目标
完成本单元后,您将能够:
- 定义线性回归。
- 区分相关性和线性回归的特征。
什么是线性回归?
上一个单元中,您学到相关性是指两个定量变量的关系的方向(正相关或负相关)和强度(从非常强到非常弱)。
与相关性一样,线性回归也显示两个数字变量的关系的方向和强度,但和相关性不同的是,回归采用连接散点图上的点的最佳拟合直线来根据 X 值预测 Y 值。对于相关性,X 和 Y 的值可以互换。对于回归,如果互换 X 和 Y,分析结果将随之变化。
线性回归线条
跟相关性一样,要想让回归有意义,必须:
- 使用定量变量
- 检查线性关系
- 警惕异常值
跟相关性一样,线性回归也在散点图上可视化。
散点图上的回归线条是连接散点图上的点的最佳拟合直线。换而言之,它是一条连接这些点的线条,使每个点到线条的距离最短。
为何这条线有用?如果 X 值已知,我们可以通过线性回归计算来计算或预测 Y 值。
为了更清楚地说明这一点,我们来看一个例子。
回归的例子
假设您想预测要购置 1,500 平方英尺的房子,需要多少钱。我们通过线性回归来预测。
- 把您想要预测的变量,即房价,放在 y 轴(这也叫因变量)。
- 把预测所依据的变量,即面积,放在 x 轴(这也叫自变量)。
这是一幅散点图,显示房价(y 轴)和面积(x 轴)。

该散点图显示面积越大,房子价格往往越高,但是 1,500 平方英尺的房子需要花多少钱呢?
为了帮助回答这个问题,画一条连接点的线。这就是线性回归。回归线条将帮助您预测一栋特定面积的典型房子需要多少钱。在这个例子中,您可以看到回归线条的方程式。
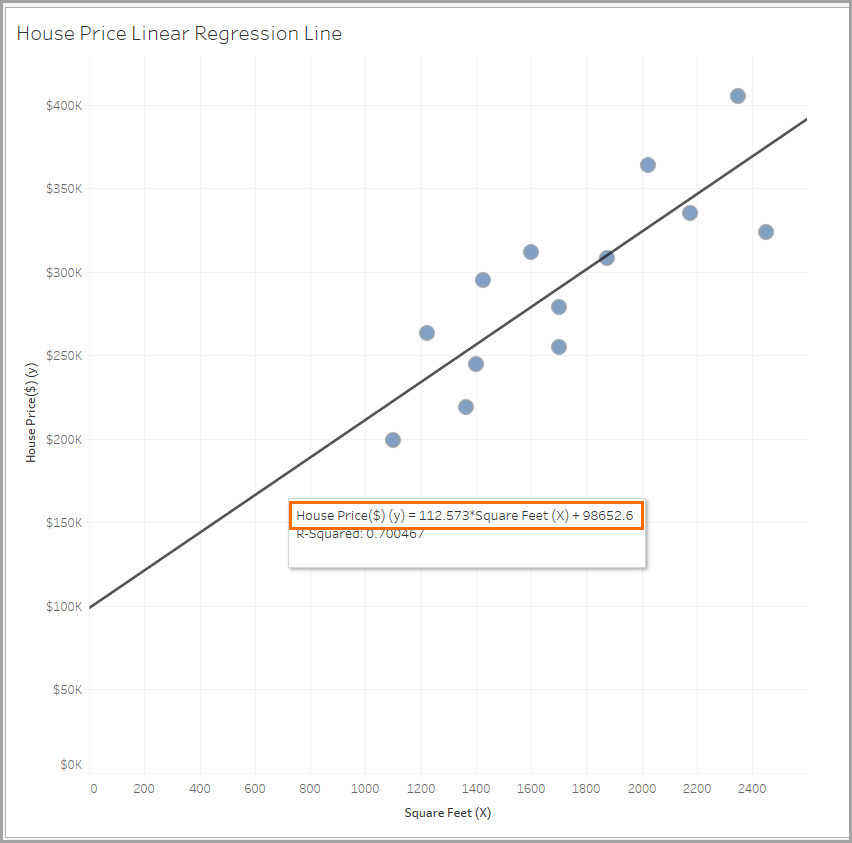
线条的方程式是 Y = 113*X + 98,653(四舍五入)。
这个方程式的含义是什么?如果您购买一个没有建筑面积的地方(比如一块空地),价格是 98,653 美元。下面是解这个方程式的步骤。
要想得到 Y,将 X 的值乘以 113,然后加上 98,653。在这个例子中,我们在看零建筑面积,因此 X 的值是 0。
- Y = (113 * 0) + 98,653
- Y = 0 + 98,653
- Y = 98,653
98,653 这个值叫做 y 截距,因为这是线条与 y 轴的交叉点或截线。它是 X 等于 0 时 Y 的值。
数字 113 是线条的斜度。斜度是描述线条的方向和陡度的数字。在这个例子中,斜度预测,面积每增加一平方英尺,房价将提高 113 美元。
因此,1,500 平方英尺的房子需要花费的钱是:
Y = (113 * 1500) + 98,653 = 268,153美元
再看一下这张散点图。蓝色标记是实际数据。您可以看到拥有 1,100 到 2,450 平方英尺之间的房子的数据。

请注意该方程式不能用来预测所有房子的价格。由于 5,000 平方英尺的房子和 10,000 平方英尺的房子都在实际数据范围之外,因此使用该方程式以那些值进行预测时您需要特别注意。
r 平方值
除了这个例子中的方程式,我们还可以看到一个 r 平方值(也叫决定系数)。

这个值从统计学上衡量数据与回归线条的接近程度,或者模型与您的观察的匹配程度。如果数据完美地落在线条上,r 平方值将是 1,即 100%,表示您的模型完美匹配(所有观察的数据点都在线条上)。
对于房价数据,r 平方值是 0.70,即 70%。
线性回归与相关性比较
现在您可能在疑惑如何区分线性回归和相关性。请看下表关于每个概念的总结。
线性回归 |
相关性 |
|---|---|
显示线性模型和预测,根据 X 预测 Y。 |
显示两个值之间的线性关系。 |
通过 r 平方来衡量模型可以解释的方差百分比。 |
通过 r 来衡量相关性的强度和方向。 |
不把 X 和 Y 用作可以互换的值(因为 Y 是根据 X 预测的)。 |
把 X 和 Y 用作可以互换的值。 |
熟悉相关性和回归的统计学概念有助于您通过考察关系来深入挖掘和了解您在使用的数据。
资源
