Fazer inferências
Objetivos de aprendizagem
Após concluir esta unidade, você estará apto a:
- Descrever o objetivo dos testes de hipótese.
- Definir o uso e as limitações dos valores P nos testes de hipótese.
Introdução
Na unidade anterior, você viu conceitos em torno do uso da variação e da distribuição normal para explorar, interpretar e se comunicar com dados. Você também viu intervalos de confiança como um exemplo de inferência.
Nesta unidade, você continuará a aprender sobre inferência. A inferência é o processo de tirar conclusões sobre uma população com base em uma amostra dos dados. É útil porque, na maioria dos casos, não é viável obter todas as medidas em determinada população.
Em outras palavras, se temos dados para todos os membros de uma população, não precisamos fazer nenhuma inferência sobre a diferença entre grupos dentro dessa população. Quando não é possível coletar dados para cada membro individual de uma população, coletamos dados de amostra e, em seguida, fazemos inferências.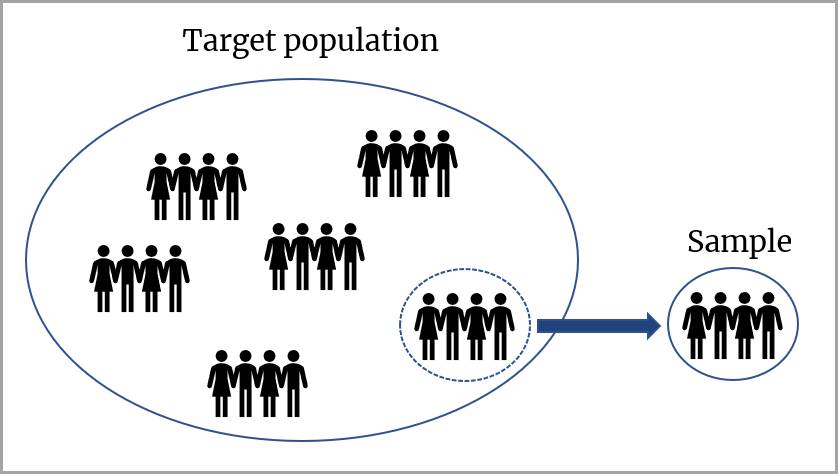
Em seu livro Avoiding Data Pitfalls (Evitando armadilhas nos dados), o autor Ben Jones, fundador e CEO da Data Literacy, LLC e membro da Tableau Community, aponta que o censo nos Estados Unidos acontece apenas uma vez por década devido ao quão caro e complicado é tentar contar "cada pessoa em cada estrutura residencial em todo o país, e tal iniciativa não está livre de preconceito e erro". Como a maioria das organizações não tem recursos financeiros ou humanos iguais aos do Governo Federal dos EUA, elas baseiam suas decisões em inferências feitas com a análise de amostras de dados.
Testes de hipótese
Muitos tipos de organizações usam testes de hipótese. Algumas empresas, por exemplo, usam testes de hipótese para controle de qualidade a fim de ver se determinado produto atende a um padrão ou para comparar novos e antigos métodos de vendas.
Pesquisas médicas também frequentemente baseiam inferências em amostras de dados. Imagine que uma empresa de biotecnologia fabricou uma nova droga para mitigar uma doença. Para determinar se a medicação funciona, um experimento controlado precisa ser realizado. Como não é possível experimentar em cada pessoa que tem a doença, um subconjunto de pessoas com a doença são sondadas aleatoriamente para testes.
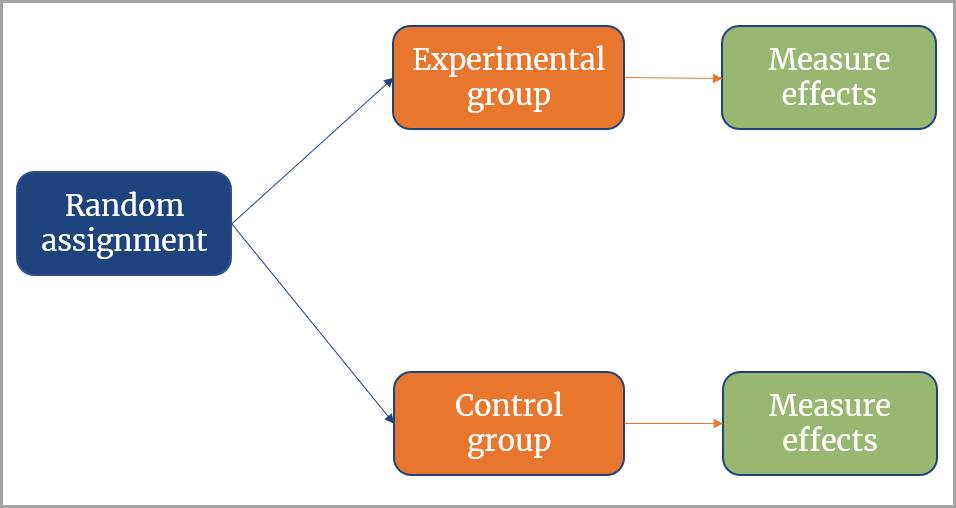
Dentro dessa amostra, o grupo experimental recebe o tratamento e o grupo de controle recebe um placebo em vez da medicação. Os grupos são atribuídos aleatoriamente para que eventuais diferenças nos desfechos de saúde possam ser atribuídas à intervenção da pesquisa.
São definidos testes para ambos os grupos e medições são feitas. Ao testar as diferenças entre os dois grupos, os pesquisadores decidem quão distantes os resultados precisam estar para determinar se os resultados de saúde para o grupo experimental e o grupo de controle são significativamente diferentes.
Os pesquisadores coletam dados dos grupos de amostra e fazem os testes estatísticos apropriados. Em seguida, os pesquisadores usam esses resultados de teste para decidir se há uma diferença significativa entre os grupos. Uma vez obtidos os dados, os pesquisadores precisarão fazer inferências sobre a população em geral, ou seja, cada pessoa que tem a doença. Isso é chamado de teste de hipótese.
O teste de hipótese começa com a criação de afirmativas de hipótese nulas e alternativas.
- A hipótese nula afirma que a medicação não terá impacto nos resultados de saúde. Ela propõe que aqueles que receberão o tratamento não terão desfechos diferentes daqueles que não receberão.
- A hipótese alternativa afirma que haverá diferença nos resultados de saúde. Ela propõe que aqueles que receberão a medicação apresentarão melhores resultados de saúde do que aqueles que não a receberão.
Os testes de hipótese começam assumindo que a hipótese nula é verdadeira. Os testes visam a entender a probabilidade de encontrar resultados que serão pelo menos tão bons quanto no experimento, assumindo que a nula seja verdadeira.
Em outras palavras, se houver uma pequena probabilidade de que os resultados sejam tão bons quanto se a nula for verdade, então haverá indícios para apoiar a hipótese alternativa. Se houver uma grande probabilidade de que os resultados sejam tão bons se a nula for verdade, então não haverá indícios suficientes para apoiar a hipótese alternativa, e os pesquisadores deverão tentar novamente com uma nova fórmula.
Os testes de hipótese levam em conta o número de amostras, o tamanho da diferença medida e a quantidade de variação observada em cada grupo.
O resultado numérico de um teste de hipótese (a probabilidade de que a hipótese nula seja verdadeira) é chamado de valor P. Um valor P ajuda a determinar se a hipótese nula deve ser rejeitada ou não. Neste caso, rejeitar a hipótese nula significa que o tratamento funcionaria na população em geral. Um pequeno valor P indica que há evidências suficientes para rejeitar a hipótese nula e apoiar a hipótese alternativa.
É importante notar, no entanto, que o valor P não prova nem refuta nada. Um alto valor P não prova que a hipótese nula é válida e um baixo valor P não prova que é inválida. É por isso que os valores P precisam ser considerados com cuidado.
Como usar os valores P
Em algum momento, os pesquisadores foram treinados para usar o valor P de 0,05 como corte. Em outras palavras, acreditava-se que um valor P de 0,05 ou inferior era suficiente para rejeitar a hipótese nula. O corte de 0,05 corresponde às caudas da distribuição normal. Lembre-se, intervalos de confiança de 95% correspondiam à área da distribuição normal que se enquadra em um desvio padrão de -2 ou +2 da média. O corte de 0,05 (ou 5%) corresponde à área que fica fora do desvio padrão de -2 ou +2 da média.
Esse raciocínio foi revisto nos últimos anos. No experimento de medicação, se fosse utilizado um corte mais baixo (efetivamente aumentando o intervalo de confiança acima de 95%), poderia ser mais difícil rejeitar a hipótese nula.
Por essas razões, e muitas outras, a Associação Americana de Estatística (ASA) emitiu uma declaração em 2016 que dizia: "Por si só, um valor P não fornece uma boa medida em relação a um modelo ou uma hipótese".
Os valores P também podem ser manipulados pelo tipo de dados trazidos para análise.
Para ver um exemplo de como os valores P podem ser manipulados, dê uma olhada neste exercício interativo de "p-hacking", Hack Your Way to Scientific Glory, no FiveThirtyEight, um site de agregação de pesquisas que também analisa pesquisas de opinião, política, economia e esportes.
Você foi agora apresentado à inferência, aos testes de hipótese e aos valores P. Entender esses conceitos pode ajudar você a medir, descrever, resumir, fazer comparações e tirar conclusões fundamentadas sobre seus dados.
Recursos
- Artigo: A Declaração da ASA sobre valores P: contexto, processo e propósito. The American Statistician, 2016
- Livro: Cairo, Alberto. The Truthful Art: Data, Charts, and Maps for Communication. Indianapolis, IN: New Riders, 2016
- Blog: Explicando visualizações no The New York Times, na NPR e na BBC." The Functional Art (blog), 2019. Link do blog. Acessar o site profissional de Alberto Cairo
- Artigo: Those Hurricane Maps Don’t Mean What You Think They Mean. (Esses mapas de furacões não são o que você pensa) The New York Times, 2019. Link para o artigo
- Artigo: Hack Your Way to Scientific Glory. (Hackear rumo à glória científica) FiveThirtyEight. ABC News Internet Ventures
- Livro: Jones, Ben. Avoiding Data Pitfalls: How to Steer Clear of Common Blunders When Working with Data and Presenting Analysis and Visualizations. (Evitando armadilhas nos dados: como evitar erros comuns ao trabalhar com dados e apresentar análises e visualizações) Hoboken, NJ: John Wiley & Sons, 2019
- Site da Web: Data Literacy (Letramento em dados), por Ben Jones
- Livro: Lane, David M. Introduction to Statistics. (Introdução à Estatística) Online Statistics Education: An Interactive Multimedia Course of Study, 2020 (Estudo de estatística online: um curso multimídia de estudo)