Usar histogramas para mostrar distribuições de variáveis contínuas
Objetivos de aprendizagem
Após concluir esta unidade, você estará apto a:
- Identificar formas de distribuições para variáveis contínuas.
- Descrever como usar histogramas para representar a distribuição de dados.
Na unidade anterior, você procurou uma variável discreta (as cores das balas) nas distribuições. Você aprendeu que variáveis discretas têm valores separados e distintos, enquanto as variáveis contínuas têm valores que formam um todo ininterrupto. Nesta unidade, você explorará distribuições de variáveis contínuas e como usar histogramas para representá-las.
O exemplo a seguir é adaptado do capítulo sobre distribuições no Online Statistics Education: A Multimedia Course of Study (Ensino de estatística online: um curso multimídia de estudo). Líder do projeto: David M. Lane, Rice University.
Em uma série de 20 ensaios, um dos autores registrou seus tempos de resposta ao mover um cursor sobre um alvo. A variável "tempo de resposta" é contínua e, quando o tempo foi medido em milissegundos, nenhum dos tempos de resposta foram iguais.
O gráfico mostra esses tempos de resposta em milissegundos.
| Avaliação | Tempos de resposta, em milissegundos | Avaliação | Tempos de resposta, em milissegundos |
|---|---|---|---|
|
1. |
568 |
11. |
720 |
|
2. |
577 |
12. |
728 |
|
3. |
581 |
13. |
729 |
|
4. |
640 |
14. |
777 |
|
5. |
641 |
15. |
808 |
|
6. |
645 |
16. |
824 |
|
7. |
657 |
17. |
825 |
|
8. |
673 |
18. |
865 |
|
9. |
696 |
19. |
875 |
|
10. |
703 |
20. |
1007 |
Distribuições de frequência agrupadas dos tempos de resposta
Pense no que aprendeu sobre distribuições de frequência na unidade anterior. Se você representasse os valores de tempo de resposta na tabela acima em uma distribuição de frequência, haveria 20 valores diferentes, cada um com uma frequência de 1. Isso não é muito informativo.
Para resolver esse problema, você pode criar uma distribuição de frequência agrupada na qual tabula os tempos de resposta que ficam dentro de vários compartimentos (faixas de valores) de mesmo tamanho, como mostrado na tabela.
| Compartimento (em milissegundos) | Frequência |
|---|---|
|
500-600 |
3 |
|
600-700 |
6 |
|
700-800 |
5 |
|
800-900 |
5 |
|
900-1000 |
0 |
|
1000-1100 |
1 |
Você pode mostrar distribuições de frequência agrupadas graficamente usando um histograma. Os rótulos no eixo X são os valores médios do compartimento que representam.
Abordaremos os histogramas com mais detalhes mais tarde. Primeiro, vamos explorar as diferentes formas de distribuição e o que elas podem dizer sobre os dados de um histograma.
Formas de distribuições
As distribuições vêm em diferentes formas. As distribuições podem ser simétricas, com os valores distribuídos uniformemente pelo centro. Alternativamente, elas podem ter uma inclinação positiva com mais valores agrupados à direita, ou uma inclinação negativa com mais valores agrupados à esquerda.
Imagine que você mediu as alturas de pessoas de três grupos diferentes e criou um histograma para cada grupo a fim de mostrar a distribuição de altura das pessoas dentro desse grupo.
O tamanho do compartimento é de 2,95 polegadas, ou seja, as alturas das pessoas estão compartimentadas como 59-61,95 polegadas, 62-64,95 polegadas e assim por diante. (O Tableau Desktop criou automaticamente o tamanho do compartimento para nós.)
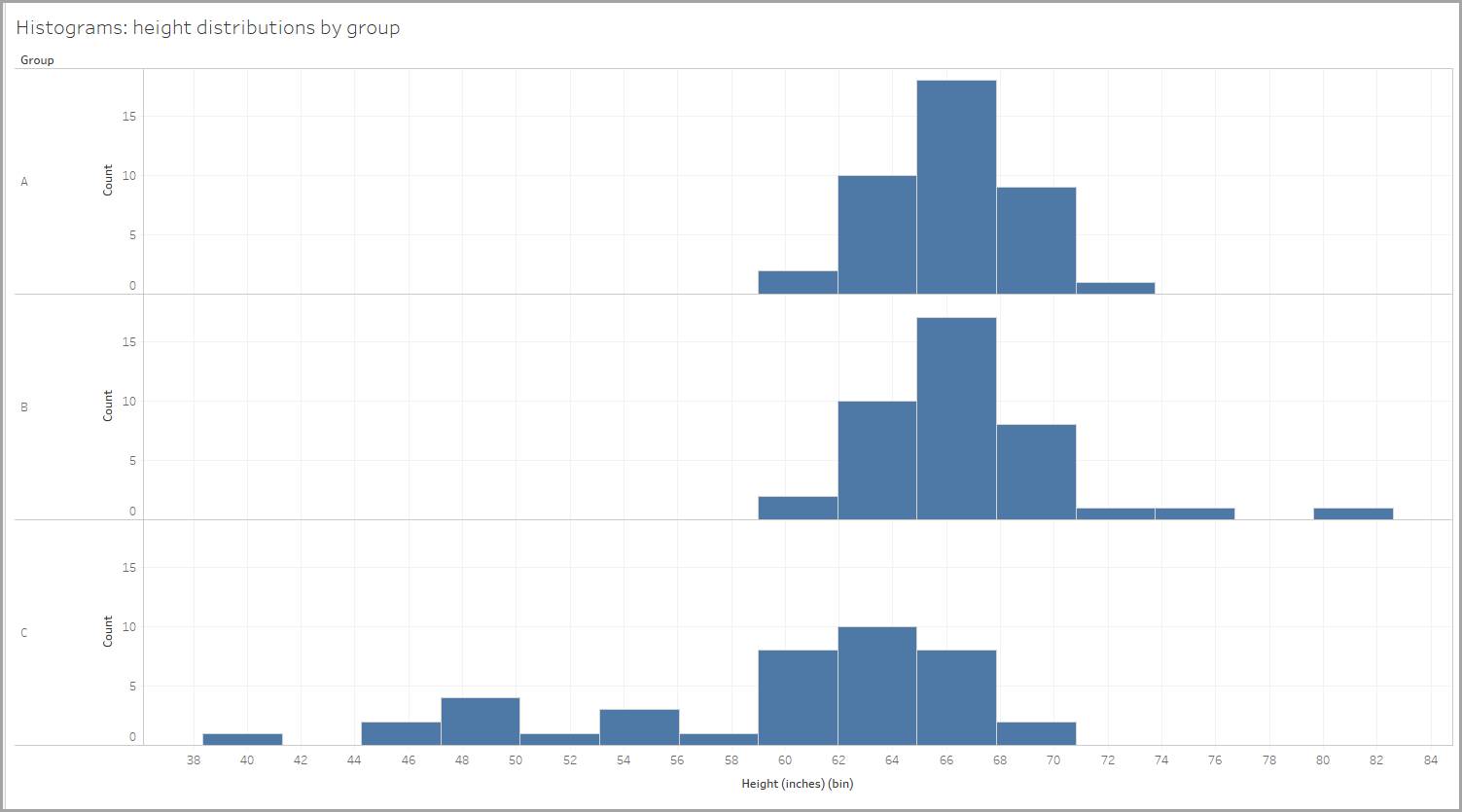
Vamos explorar a forma de cada distribuição. Em cada uma das distribuições mostradas abaixo, observe que os valores médios (média) e medianos (o valor do meio dos pontos de dados) determinam a forma.
Distribuições simétricas
Em nosso exemplo, a distribuição de altura para um dos grupos é quase simétrica. Se você dobrasse ao meio, os dois lados chegariam perto de corresponder perfeitamente.
Em uma distribuição totalmente simétrica, o centro dos dados é tanto a média quanto a mediana (o valor do meio dos pontos de dados) porque esses valores são iguais. O centro dos dados é representado por ambos os valores, e a disseminação dos dados se estende igualmente a ambos os lados do centro.
Distribuições de assimetria positiva
Algumas distribuições não são simétricas. Se os dados em uma distribuição se espalham mais na direção positiva do que na direção negativa, é uma distribuição com uma assimetria positiva. Uma assimetria positiva também é chamada de assimetria à direita porque os dados se estendem para a direita. A "cauda" à direita é mais longa. Quando uma distribuição tem assimetria positiva, a mediana é menor do que a média.
Por exemplo, imagine uma cidade cujos moradores incluam vários bilionários. Os altos rendimentos desses bilionários distorceriam a renda média da cidade. O rendimento médio pareceria maior do que o real. Para refletir verdadeiramente a saúde econômica de todos os moradores da cidade, a renda mediana seria a melhor escolha.
Da mesma forma, ao olhar para nossos dados de altura, um grupo mostra uma inclinação positiva devido à presença de três indivíduos que mediram perto ou mais que 72" (1,82 m). Suas alturas tornam a média mais alta. Usar a mediana para obter uma imagem da altura do grupo seria uma escolha melhor aqui também.
Distribuições de assimetria negativa
Outra distribuição assimétrica é uma distribuição de assimetria negativa. Os dados em uma distribuição de assimetria negativa se espalham mais na direção negativa do que na direção positiva. Uma assimetria negativa também é chamada de assimetria à esquerda porque os dados se estendem para a esquerda. A "cauda" esquerda é mais longa. Quando uma distribuição tem assimetria negativa, a mediana é maior que a média.
Por exemplo, imagine uma turma de 20 alunos. Nessa aula, há dois alunos que nunca frequentaram as aulas nem concluíram nenhuma atribuição. Esses dois alunos ganharam uma nota final de 0,0. Suas notas 0,0 distorceriam os resultados da nota média obtida pela turma, fazendo com que o desempenho médio dos alunos parecesse menor do que a realidade. Para refletir verdadeiramente o sucesso dos alunos nessa turma, a nota mediana obtida seria uma escolha melhor.
Da mesma forma, ao olhar para nossos dados de altura, um grupo mostra uma assimetria negativa devido à presença de indivíduos que mediram menos de 60" (1,52 m). Suas alturas tornam a média menor.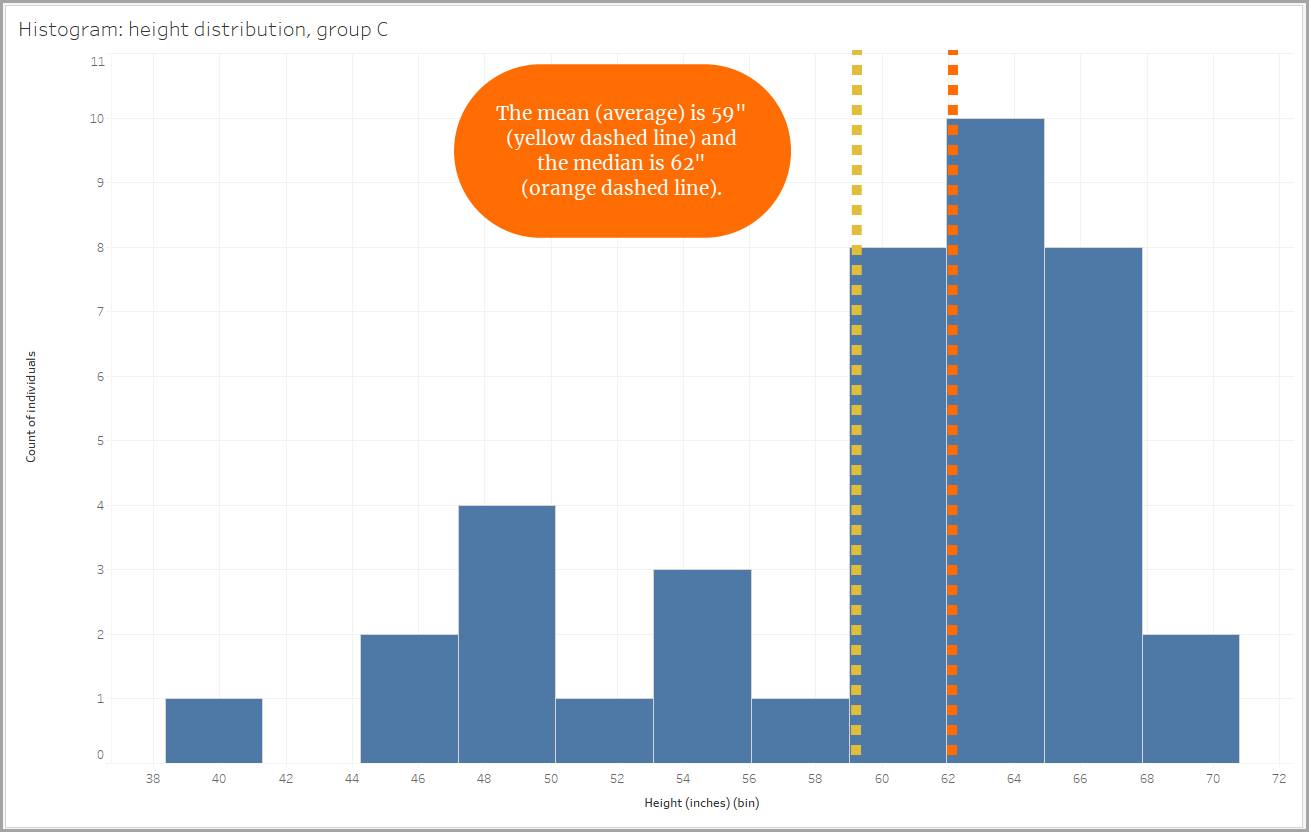
Histogramas
Todos os gráficos que você explora nesta unidade são histogramas. Um histograma se parece com um gráfico de barras, mas ele agrupa valores para uma variável contínua em faixas de tamanho igual, ou compartimentos.
Esse histograma usa um conjunto de dados com informações sobre atletas olímpicos. Uma das variáveis no conjunto de dados contém idades dos atletas, de 18 a 90 anos. O histograma permite ver como os atletas se dividem em diferentes faixas etárias.
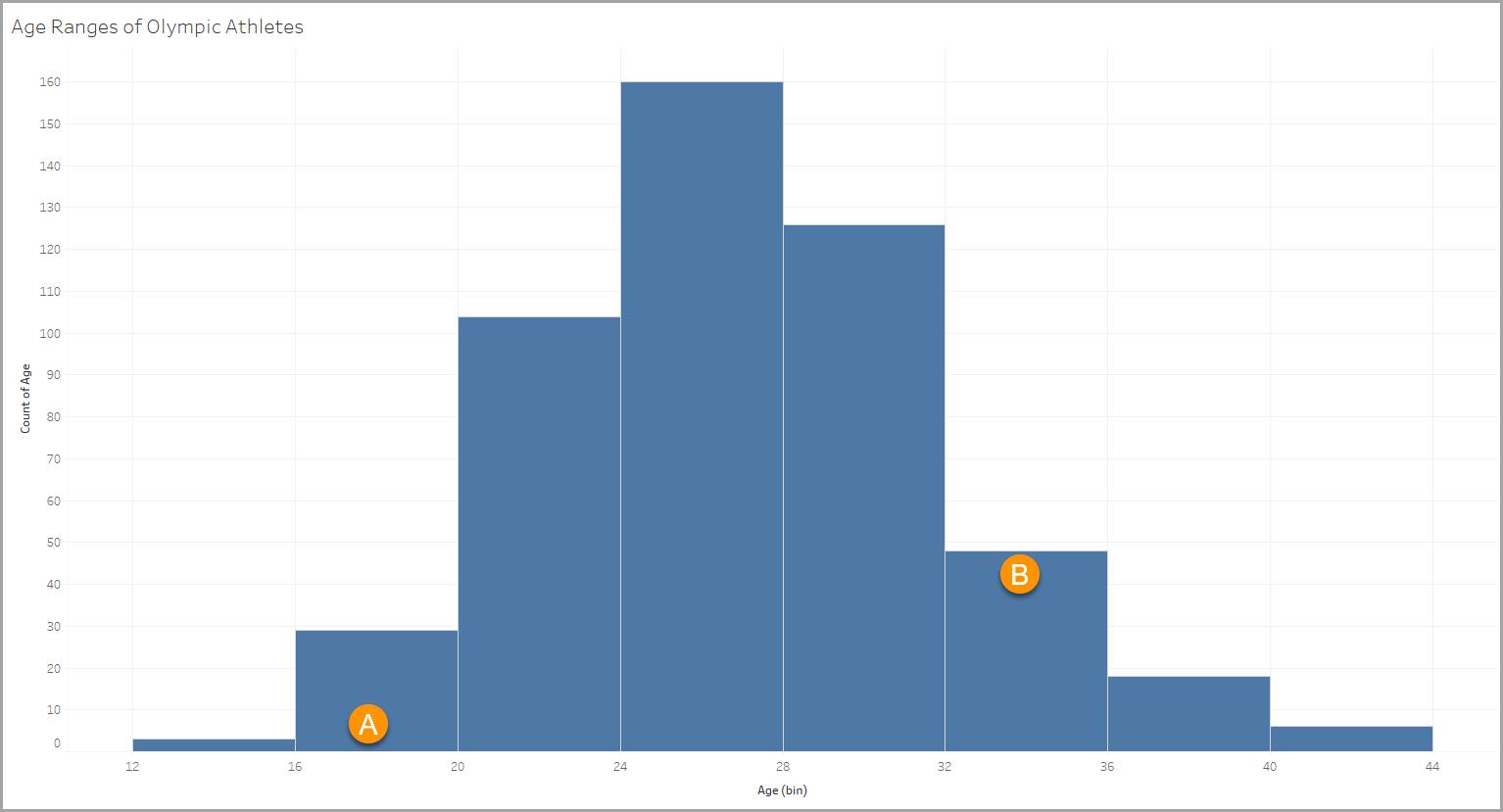
Compartimentos
Cada compartimento é definido por uma faixa etária de quatro anos, por exemplo, 12-15, 16-19 (A), 20-23, 24-27 e assim por diante.
Colunas
Cada coluna representa a contagem de itens que atendem aos critérios do compartimento (neste caso, a faixa etária). No nosso exemplo, há 48 atletas na faixa etária de 32 a 35 anos (B).
Agora você deu uma olhada nas distribuições para variáveis contínuas organizadas como histogramas. Na próxima unidade, você aprenderá sobre a visualização de distribuições de variáveis contínuas usando diagramas de caixa.
