Usar diagramas de caixa para mostrar distribuições de variáveis contínuas
Objetivos de aprendizagem
Após concluir esta unidade, você estará apto a:
- Descrever como usar diagramas de caixa para representar a distribuição de dados.
- Criar um diagrama de caixa.
Até agora você analisou várias maneiras de ver distribuições de variáveis. Nesta unidade, você aprenderá sobre outro gráfico importante, chamado diagrama de caixa. Introduzido na década de 70 pelo matemático americano John Tukey, os diagramas de caixa são uma maneira visualmente concisa de ver e comparar distribuições de dados.
As caixas em um diagrama de caixa mostram os 50% do meio dos dados. Esses dados se estendem do percentil 25 para o percentil 75, com a mediana no percentil 50.
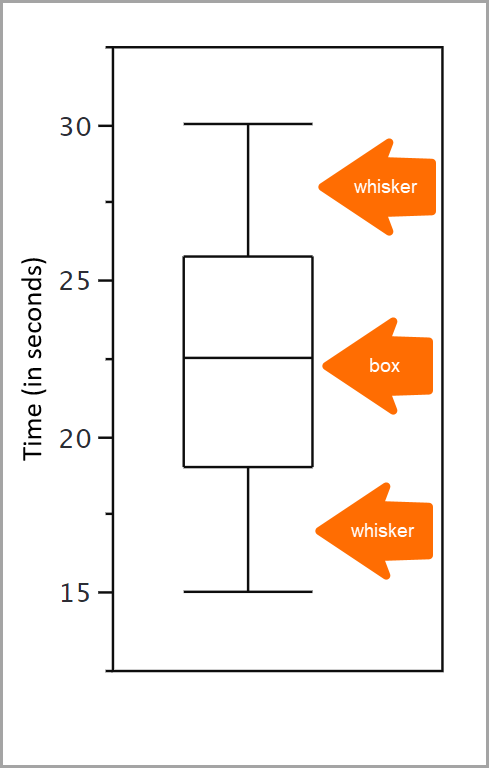
Um percentil expressa como uma pontuação se compara a outras pontuações dentro do mesmo conjunto de dados. Por exemplo, você faz um teste para medir seu nível de introversão. Por si só, sua pontuação de introversão é difícil de interpretar. Você quer ver como sua pontuação se compara com a dos outros e saber a porcentagem de pessoas com menor pontuação de timidez do que a sua. Essa porcentagem é um percentil. Se 65% das outras pessoas que fizeram o teste pontuaram como menos tímidos que você, sua pontuação está no percentil 65.
Para revisar, a caixa em um diagrama de caixa mostra os 50% do meio dos dados, ou o percentil de 25 a 75. Mas e os dados que estão fora disso? É aí que as retas entram. Plotadas fora da caixa, as retas são linhas verticais que terminam em um curso horizontal. Eles fornecem insights sobre valores que não estão dentro desses 50% do meio dos dados (a caixa), incluindo discrepâncias. As discrepâncias podem ser entendidas como observações atípicas e pouco frequentes, ou como valores que têm um desvio extremo do centro de uma distribuição.
Analisamos todos esses conceitos com mais detalhes mais tarde na unidade.
Criar um diagrama de caixa
O seguinte exemplo de diagrama de caixa é adaptado do capítulo de David M. Lane sobre diagramas de caixa em Online Statistics Education: A Multimedia Course of Study (Ensino de estatística online: um curso multimídia de estudo). Líder do projeto: David M. Lane, Rice University.
O autor usou um experimento em sala de aula com 31 alunos. Cada um dos alunos recebeu uma página de 30 retângulos coloridos e sua tarefa era nomear as cores o mais rápido possível.
Seus tempos, em segundos, foram registrados como mostrado na tabela a seguir.
|
14 |
17 |
18 |
19 |
20 |
21 |
|
15 |
17 |
18 |
19 |
20 |
22 |
|
16 |
17 |
18 |
19 |
20 |
23 |
|
16 |
17 |
18 |
20 |
20 |
24 |
|
17 |
18 |
18 |
20 |
21 |
24 |
| 29 |
Vamos usar esse conjunto de dados para criar um diagrama de caixa. Aqui está uma visão geral dos passos que você precisa seguir para criá-lo.
- Calcule os percentis.
- Plote a caixa de acordo com os percentis.
- Determine o tamanho da etapa.
- Adicione as retas.
- Adicione o valor externo.
Calcular percentis
Lembre-se que as caixas nos diagramas de caixa se estendem do percentil 25 até o percentil 75 dos dados. O percentil 50 é desenhado dentro da caixa. A parte inferior da caixa (chamada de dobradiça inferior) é o percentil 25 e a parte superior da caixa (chamada de dobradiça superior) é o percentil 75.
Nas etapas seguintes, vamos usar uma linha numérica para ver os percentis.
-
Liste as pontuações de menor para maior.
-
Determine a mediana, ou o valor central. O valor médio aparece no meio do caminho entre o início e o fim da sequência de números. Para uma sequência de 31 valores, o meio do caminho significaria que há 15 valores antes da mediana e 15 valores depois dela. Assim, o valor médio é de 19.
-
Determine o percentil 25. O valor do percentil 25 aparece no meio do caminho entre o início da sequência e a mediana. No nosso exemplo de 31 valores, essa localização intermediária tem 7 valores antes dele e 7 valores entre ele e a mediana. Assim, o valor do percentil 25 é de 17.
-
Determine o percentil 75. O valor do percentil 75 aparece no meio do caminho entre a mediana e o final da sequência. Para nossa lista de 31 valores, essa localização intermediária tem 7 valores entre ele e a mediana, e 7 valores entre ele e o final da sequência. Assim, o valor do percentil 75 é de 20.
Plote a caixa de acordo com os percentis
Vamos ligar esses valores e plotar a caixa.
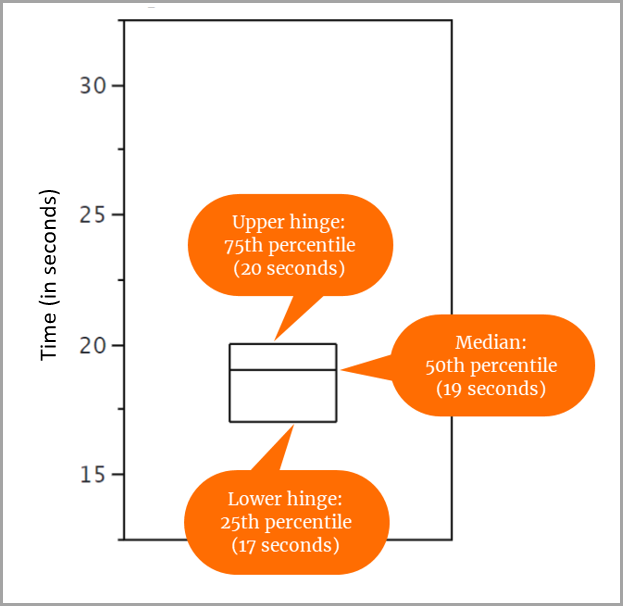
Para nosso conjunto de 31 pontuações, determinamos que:
- O percentil 25 é 17.
- O percentil 50 (ou mediana) é 19.
- O percentil 75 é 20.
Ou seja, você desenha a caixa desta forma.
- O percentil 25 (dobradiça inferior) se alinha com 17 no eixo Y.
- O percentil 50 (mediana) se alinha com 19 no eixo Y.
- O percentil 75 (dobradiça superior) se alinha com 20 no eixo Y.
Os 50% do meio dos valores dos dados aparecem na caixa.
Nota: os valores entre o percentil 25 até a mediana também são chamados de segundo quartil, e os valores do percentil 51 (logo após a mediana) até o percentil 75 são chamados de terceiro quartil. Valores menores que o percentil 25 também são chamados de primeiro quartil, e valores acima do percentil 75 também são chamados de quarto quartil. Use retas e outras marcas para mostrar valores de primeiro e quarto quartil.
Determinar o tamanho da etapa
Agora se prepare para plotar retas acima e abaixo da caixa a fim de dar informações adicionais sobre o espalhamento dos dados. A colocação da reta é determinada por passos, que são definidos como 1,5 x IQR. IQR é a distância interquartílica.
Isso parece complicado, mas a IQR simplesmente se refere à diferença entre o valor da dobradiça superior (percentil 75) e o valor da dobradiça inferior (percentil 25). Lembre-se, os 50% do meio dos valores de dados estão na caixa delimitada por esses valores.
Em nosso conjunto de pontuações, o valor da dobradiça superior é 20 e o valor da dobradiça inferior é 17. Então, a IQR é 20 menos 17, ou 3.
Para determinar o tamanho do nosso passo, multiplique 3 (a IQR) por 1,5 para obter 4,5 como nosso tamanho de passo.
Adicionar as retas
Para entender como plotar as retas, vamos primeiro olhar para alguns termos e como eles se aplicam às pontuações em nosso exemplo.
Onde vão parar as retas?
Você pode desenhar retas da dobradiça superior até o valor adjacente superior e da dobradiça inferior até o valor adjacente inferior.
As retas não vão até os valores externos. Você representa um valor externo com um pequeno o e um valor muito fora com um asterisco (*).
Para nossos dados de pontuação, as retas estendem-se do valor da dobradiça superior (20) até o valor adjacente superior (24) e do valor da dobradiça inferior (17) até o valor adjacente inferior (14).
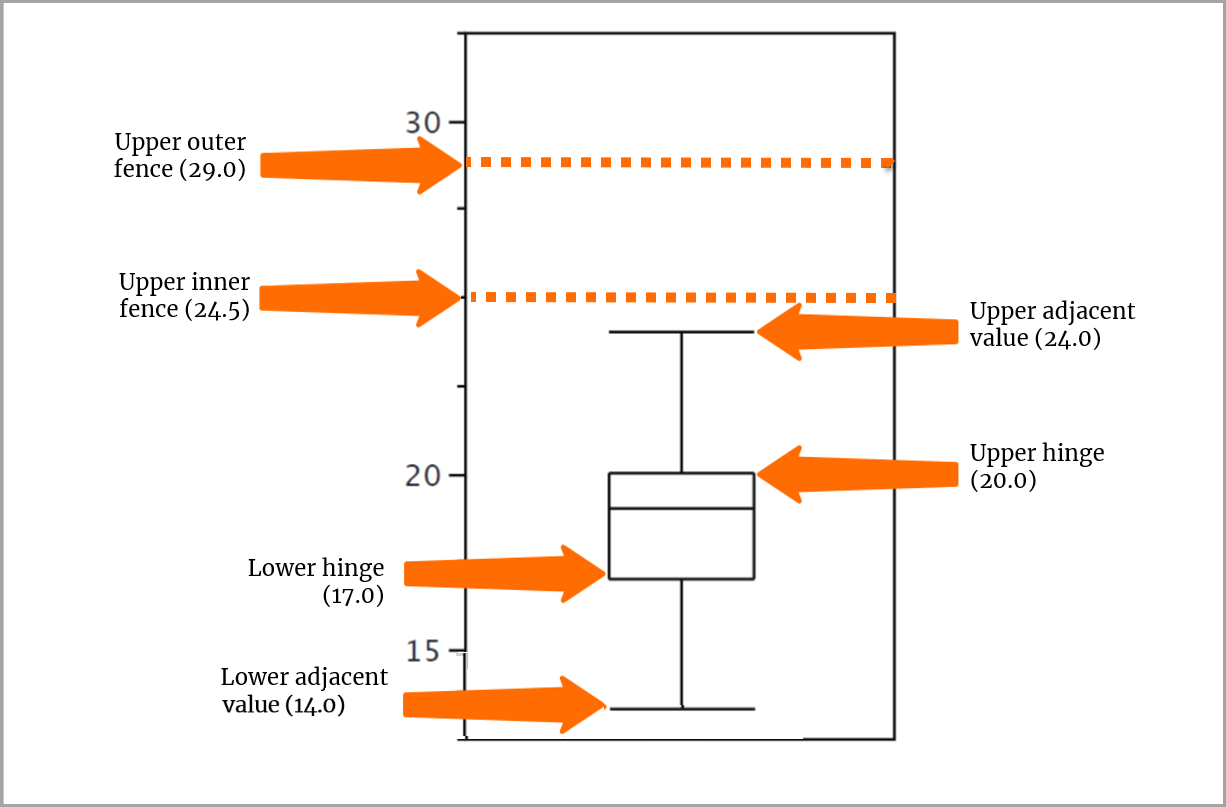
Adicionar o valor externo
Um valor além de uma cerca interna, mas não além de uma cerca externa, é um valor externo. Temos um desses valores em nosso conjunto de pontuações, 29, que coincide com o valor da cerca externa, mas não está além dela. Você usa um pequeno o para retratar esse valor.
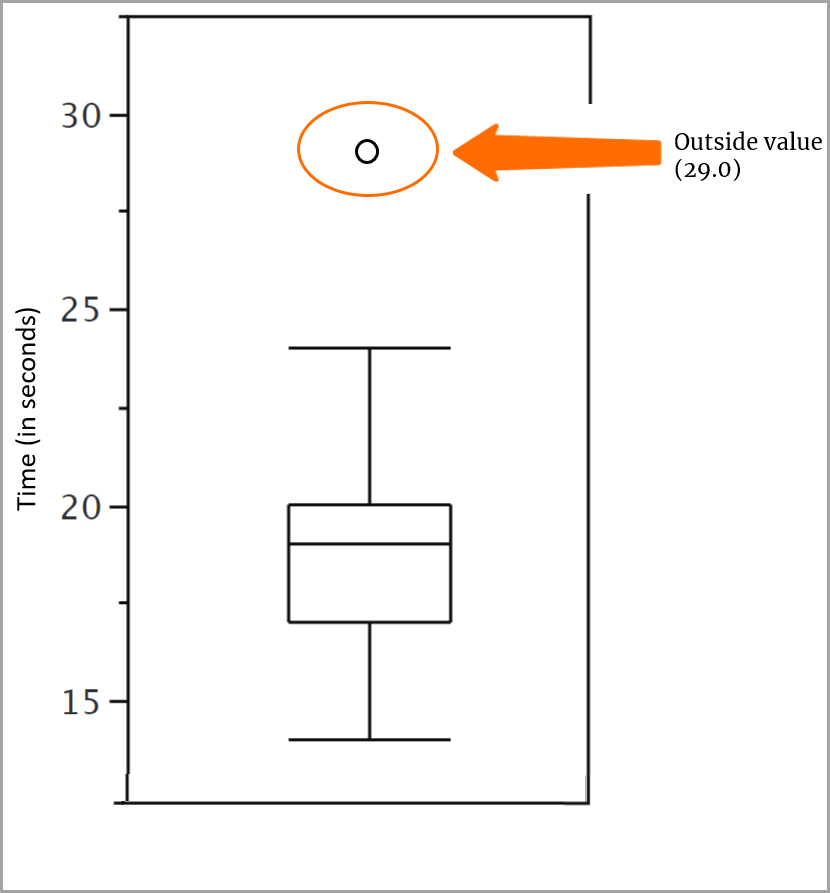
E, com isso, seu diagrama de caixa está completo!
Diagramas de caixa X histogramas
Você deve estar se perguntando como os diagramas de caixa diferem dos histogramas na exibição de distribuições.
- Os histogramas usam compartimentos para plotar a frequência dos valores.
- Nos diagramas de caixa, os 50% do meio dos dados aparecem na caixa e as discrepâncias (se houver) são plotadas fora das retas.
Para ter uma ideia de como isso fica, vamos voltar aos dados mostrando as formas de distribuição das alturas das pessoas. Compare como os dados são exibidos em um histograma e em um diagrama de caixa.
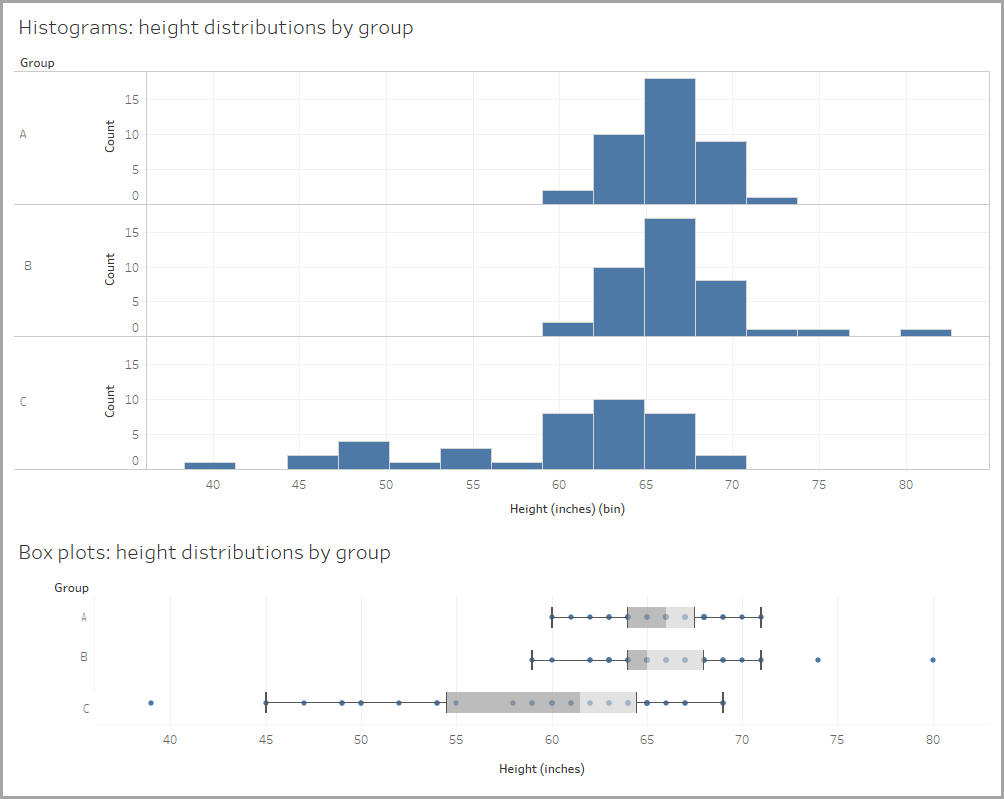
Observe como o diagrama de caixa usa menos espaço; isso pode facilitar a comparação de distribuições. Três distribuições lado a lado são mais fáceis de comparar com diagramas de caixa do que com histogramas. Vamos ver mais alguns exemplos.
Agora você tem uma compreensão de como as distribuições podem ajudá-lo a explorar, entender e se comunicar com dados.
