Examinar correlação em dados
Objetivos de aprendizagem
Após concluir esta unidade, você estará apto a:
- Definir correlação.
- Distinguir entre correlações fortes e fracas.
Jornada rumo à fluência em dados
O letramento em dados é a base para usar e se comunicar com dados com facilidade.
O módulo Noções básicas de letramento em dados descreve variáveis quantitativas como características numericamente mensuráveis, como número de horas gastas assistindo televisão todos os dias, velocidade medida em quilômetros por hora, total de metros de chuva anuais em uma cidade, vendas em dólares e valor gasto em marketing.
Quando você está examinando relacionamentos entre seus dados, como determina o grau de proximidade de duas variáveis, por exemplo, vendas e valor gasto em marketing? Você pode usar uma variável para prever a outra?
Correlação e regressão são técnicas importantes usadas para descobrir tendências e fazer previsões. Embora existam outras maneiras importantes usadas na análise, nos concentramos na maneira mais simples usada na IA e na análise – correlação e regressão lineares.
Nesta unidade, você ganhará familiaridade com o conceito de correlação, que descreve se e com que proximidade duas variáveis se movem em relação uma à outra. Você ganhará uma apreciação de como a correlação mede a associação, mas não prova causalidade. Na próxima unidade, você explorará como a regressão linear pode ser usada para calcular ou prever o valor de uma variável com base em outra, além de medir o quão bem esse modelo se adequa aos seus dados.
O que é correlação?
Correlação é uma técnica que pode mostrar se e com que grau de solidez pares de variáveis quantitativas estão relacionados.
Esta unidade discute a correlação de Pearson. Há outras correlações não lineares que não são abordadas aqui.
Por exemplo, o número de calorias diárias consumidas e o peso corporal têm relação? As pessoas que consomem mais calorias pesam mais? A correlação pode dizer quão fortemente o peso das pessoas está relacionado à sua ingestão de calorias.
A correlação entre peso e ingestão calórica é um exemplo simples, mas às vezes os dados com os quais você trabalha podem não ter as relações que espera. Outras vezes, você pode suspeitar de correlações sem saber quais são as mais fortes. A análise de correlação ajuda você a entender seus dados.
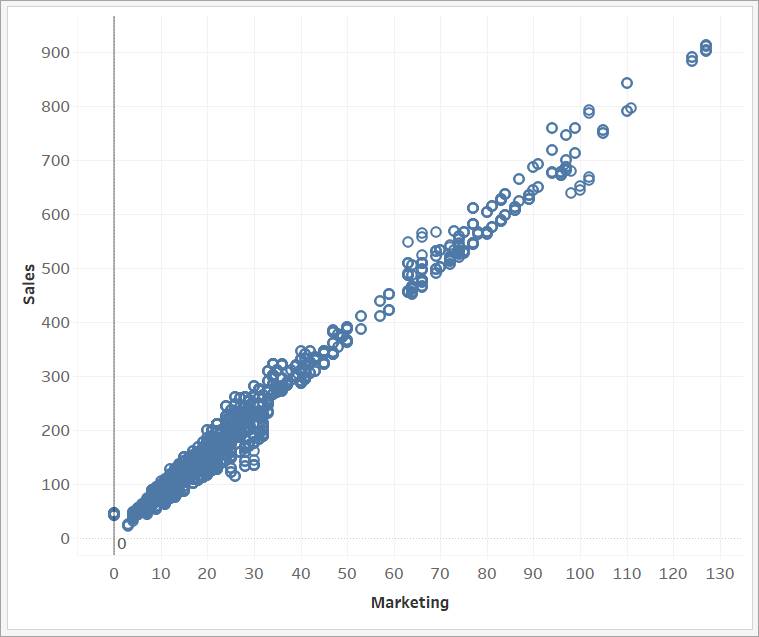
Quando você começa sua análise de correlação, pode criar um gráfico de dispersão para investigar o relacionamento entre duas variáveis quantitativas. As variáveis são plotadas como coordenadas cartesianas, marcando a distância de cada ponto de dados no eixo x horizontal e no eixo y vertical. No gráfico de dispersão abaixo, você vê a relação entre as vendas e o valor gasto em marketing. Parece que há uma correlação: à medida que uma variável sobe, a outra parece subir também.
Os conceitos nesta unidade são adaptados do trabalho online de David M. Lane, Introdução à Estatística (domínio público).
Correlação X Causalidade
Agora que você sabe como a correlação é definida e como ela é representada graficamente, vamos discutir como entender melhor a correlação.
Primeiro, é importante saber que correlação nunca prova causalidade.
A correlação de Pearson nos diz apenas o grau de solidez do relacionamento linear entre um par de variáveis quantitativas. Ela não explica como ou por que elas estão relacionadas.
Por exemplo, as vendas de aparelhos de ar-condicionado se correlacionam com as vendas de protetor solar. As pessoas não estão comprando aparelhos de A/C porque compraram protetor solar ou vice-versa. A causa de ambas as compras é o clima quente.
Como a correlação é medida?
A correlação de Pearson, também chamada de coeficiente de correlação, é usada para medir a força e a direção (positiva ou negativa) da relação linear entre duas variáveis quantitativas. Quando a correlação é medida em uma amostra de dados, o símbolo utilizado é a letra r. O r de Pearson pode variar de -1 a 1.
Quando r = 1, há uma relação linear positiva perfeita entre as variáveis, o que significa que ambas as variáveis se correlacionam perfeitamente à medida que os valores aumentam. Quando r = -1, há uma relação linear negativa perfeita entre as variáveis. Em uma correlação negativa perfeita, quando uma variável aumenta, a outra variável diminui com a mesma magnitude. Quando r = 0, não é indicada nenhuma relação linear entre as variáveis.
Com dados reais, você não esperaria ver r valores de -1, 0 ou 1.
Geralmente, quanto mais perto r é de 1 ou -1, mais forte a correlação, como mostrado na tabela a seguir.
| r = | Correlação |
|---|---|
|
0,90 a 1 ou -0,90 a -1 |
Correlação muito forte |
|
0,70 a 0,89 ou -0,70 a -0,89 |
Correlação forte |
|
0,40 a 0,69 ou -0,40 a -0,69 |
Correlação limitada |
|
0,20 a 0,39 ou -0,20 a -0,39 |
Correlação fraca |
|
0 a 0,19 ou 0 a -0,19 |
Muito fraca ou sem correlação |
alguns recursos sobre este tema categorizam correlações simplesmente como fortes, limitadas ou fracas.
Condições para correlação linear
Para que as correlações sejam significativas, você precisa considerar algumas condições: elas devem usar variáveis quantitativas, descrever relacionamentos lineares e levar em consideração o efeito de eventuais discrepâncias. Você deve verificar essas condições antes de executar uma análise de correlação.
Em 1973, um estatístico chamado Francis Anscombe desenvolveu o Quarteto de Anscombe para mostrar a importância de grafar dados visualmente em vez de simplesmente executar testes estatísticos. Todas as quatro visualizações em seu quarteto mostram a mesma equação da linha de tendência. O quarteto ilustra por que as visualizações são tão importantes: elas nos ajudam a identificar tendências dentro de nossos dados que podem ficar escondidas com testes estatísticos.
No exemplo abaixo, apenas o gráfico de dispersão superior esquerdo no quarteto atende aos critérios de ser linear sem nenhuma discrepância. O gráfico de dispersão no canto superior direito não está mostrando um relacionamento linear, e um modelo não linear seria mais apropriado. Os dois gráficos de dispersão na parte inferior têm discrepâncias que podem afetar drasticamente os resultados.
Agora que você está mais familiarizado com os conceitos em torno da técnica estatística de correlação, está pronto para a próxima unidade, em que aprenderá sobre regressão linear.