히스토그램을 사용하여 연속 변수 분포 표시
학습 목표
이 유닛을 완료하면 다음을 수행할 수 있습니다.
- 연속 변수에 대한 분포의 모양을 식별할 수 있습니다.
- 데이터의 분포를 나타내기 위해 히스토그램을 사용하는 방법을 설명할 수 있습니다.
이전 유닛에서는 이산 변수(사탕 색상)에 대한 분포를 살펴보았습니다. 이산 변수는 분리되고 구별되는 값을 갖는 반면, 연속 변수는 깨지지 않는 전체를 형성하는 값을 갖는다는 것을 배웠습니다. 이 유닛에서는 연속 변수의 분포와 히스토그램을 사용하여 표현하는 방법을 살펴봅니다.
다음 예시는 Online Statistics Education: A Multimedia Course of Study의 분포를 설명하는 챕터에서 가져온 것입니다. 프로젝트 리더: 라이스 대학교의 David M. Lane
20번의 실험에서, 저자 중 한 명은 커서를 과녁 위로 옮기면서 자신의 반응 시간을 기록했습니다. 변수 "반응 시간"은 연속적이고, 시간이 밀리초로 측정될 때, 어떤 2개의 반응 시간도 동일하지 않았습니다.
차트는 이러한 반응 시간을 밀리초 단위로 표시합니다.
실험 |
반응 시간(밀리초) |
실험 |
반응 시간(밀리초) |
|---|---|---|---|
1. |
568 |
11. |
720 |
2. |
577 |
12. |
728 |
3. |
581 |
13. |
729 |
4. |
640 |
14. |
777 |
5. |
641 |
15. |
808 |
6. |
645 |
16. |
824 |
7. |
657 |
17. |
825 |
8. |
673 |
18. |
865 |
9. |
696 |
19. |
875 |
10. |
703 |
20. |
1007 |
반응 시간의 그룹화된 빈도 분포
이전 유닛에서 빈도 분포에 대해 알아본 내용을 다시 생각해 보세요. 위의 표에서 반응 시간 값을 빈도 분포로 나타내면 20개의 서로 다른 값이 있으며 각 값은 1의 빈도를 가집니다. 별로 유익하지 않음
이 문제를 해결하려면 그룹화된 빈도 분포를 만들어 표과 같이 다양한 균등 크기의 빈(값 범위)에 속하는 반응 시간을 표로 만들 수 있습니다.
빈(밀리초) |
빈도 |
|---|---|
500–600 |
3 |
600–700 |
6 |
700–800 |
5 |
800–900 |
5 |
900–1000 |
0 |
1000–1100 |
1 |
히스토그램을 사용하여 그룹화된 빈도 분포를 그래픽으로 표시할 수 있습니다. X축의 레이블은 레이블이 나타내는 빈의 중간값입니다.

히스토그램을 좀 더 자세히 살펴보겠습니다. 먼저 히스토그램의 데이터에 대해 다른 분포 모양과 알 수 있는 내용을 살펴보겠습니다.
분포 형태
분포는 여러 가지 형태로 나타납니다. 분포는 대칭일 수 있으며, 값은 중심 주위에 균등하게 분포합니다. 또한, 더 많은 값이 오른쪽으로 치우쳐 있는 양의 왜도를 가질 수 있거나, 더 많은 값이 왼쪽으로 치우쳐 있는 음의 왜도를 가질 수 있습니다.
세 그룹의 사람들의 높이를 측정하고 각 그룹의 히스토그램을 만들어서 해당 그룹의 사람들의 키 분포를 보여준다고 상상해보세요.
빈의 크기는 2.95인치이므로 사람들의 키는 59-61.95인치, 62-64.95인치 등으로 표시됩니다. (Tableau Desktop은 자동으로 BIN 크기를 생성합니다.)
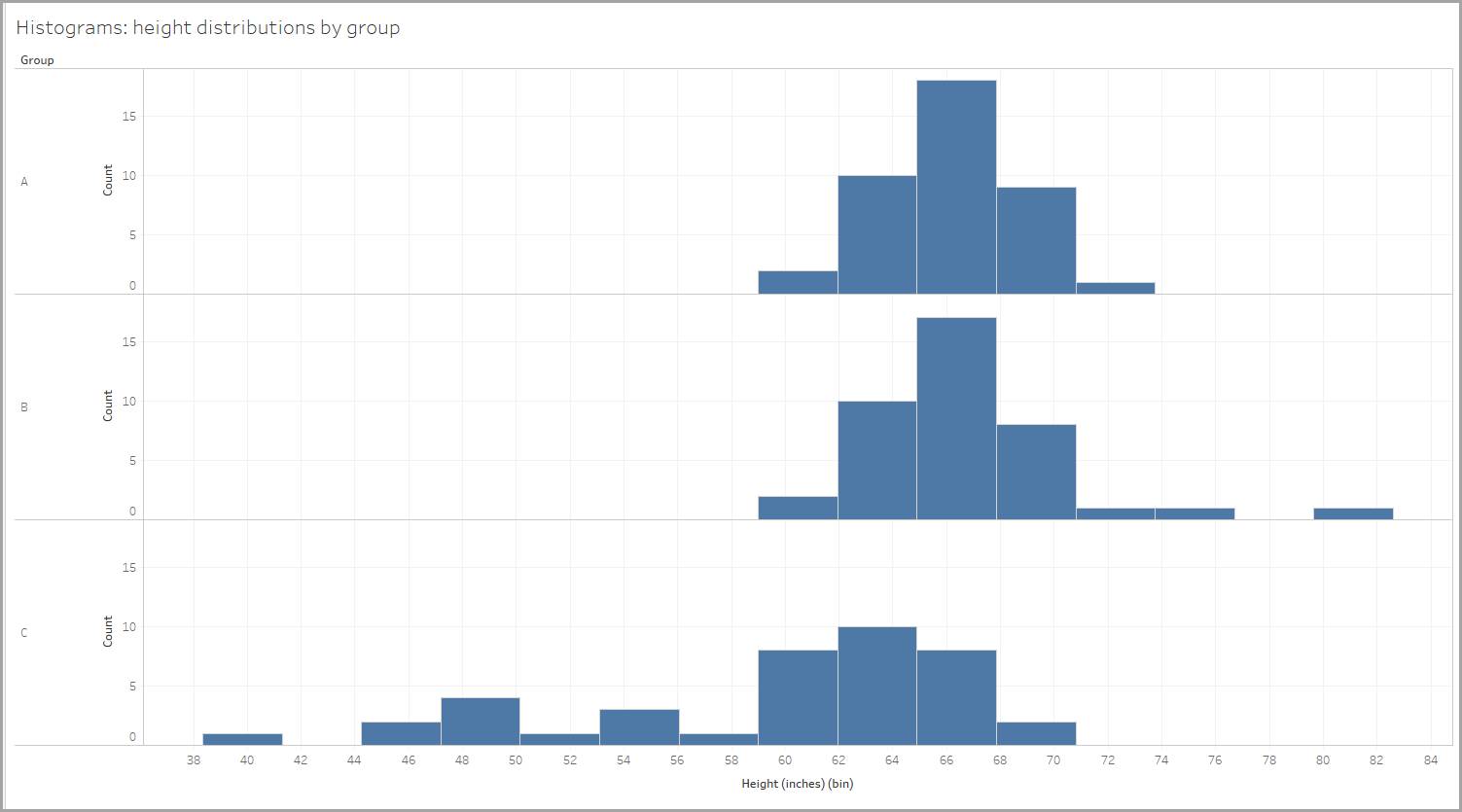
각 분포의 모양을 살펴보겠습니다. 아래 표시된 각 분포에서 평균값(평균) 및 중위수(데이터 점의 중간값) 값이 모양을 결정합니다.
대칭 분포
살펴본 예시에서, 그룹 중 하나에 대한 높이 분포는 거의 대칭적입니다. 반으로 접으면 두 면이 완벽하게 일치합니다.
완전 대칭 분포에서, 데이터의 중심은 평균값(또는 평균)과 중앙값(데이터 지점의 중간값)이 모두 같기 때문입니다. 데이터의 중심은 양 값으로 표현되며, 데이터의 확산은 중심의 양측에서 동일한 양으로 확장됩니다.
양의 왜도 분포
일부 분포는 대칭적이지 않습니다. 분포의 데이터가 음의 방향보다 양의 방향으로 더 멀리 퍼져나갈 경우 양의 왜도를 가진 분포가 됩니다. 양의 왜도는 데이터가 오른쪽으로 늘어나므로 오른쪽 왜도라고도 합니다. 오른쪽 "꼬리" 가 더 깁니다. 분포가 양수인 경우 중앙값은 평균값(또는 평균)보다 작습니다.
예를 들어, 주민이 억만장자 몇 명을 포함하는 도시를 상상해 보세요. 억만장자의 높은 소득은 도시의 평균 소득을 의미할 것입니다. 평균 소득이 정확도보다 높아 보입니다. 모든 도시 주민의 경제적 활력을 반영하기 위해서는 중위 소득이 더 나은 선택이 됩니다.
마찬가지로, 신장 데이터를 볼 때, 한 그룹은 72"(6피트)에 가깝거나 그보다 크게 측정된 세 명의 개인이 존재하기 때문에 양의 왜도를 보여줍니다. 높은 높이는 평균값을 더 높게 만듭니다. 중앙값을 사용하여 그룹의 키를 파악하는 것도 더 나은 선택이 됩니다.
음의 왜도 분포
또 다른 비대칭 분포는 음의 왜도 분포입니다. 음의 왜도 분포의 데이터는 양의 방향보다 음의 방향으로 더 멀리 퍼집니다. 데이터가 왼쪽으로 늘어나므로 음의 왜도는 왼쪽 왜도라고도 불립니다. 왼쪽 "꼬리”가 더 깁니다. 분포가 음의 왜도인 경우 중앙값이 평균값(또는 평균)보다 큽니다.
예를 들어 20명의 학생들로 구성된 수업을 상상해 보세요. 이 수업에는 수업에 참여하지 않았거나 과제를 완료하지 않은 두 명의 학생이 있습니다. 이 두 학생은 최종 성적이 0.0이었습니다. 0.0점은 수업에 대해 얻은 평균(또는 평균) 등급 결과를 왜곡하여 평균 학생의 성적이 정확한 값보다 낮게 보이게 합니다. 이 수업에서 학생들의 성취도를 제대로 반영하기 위해서는 평균 성적이 더 나은 선택이 됩니다.
마찬가지로, 신장 데이터를 볼 때 한 그룹은 60"(5피트)보다 작게 측정된 개인의 유무로 인해 음의 왜도를 보여줍니다. 낮은 키는 평균을 작게 만듭니다.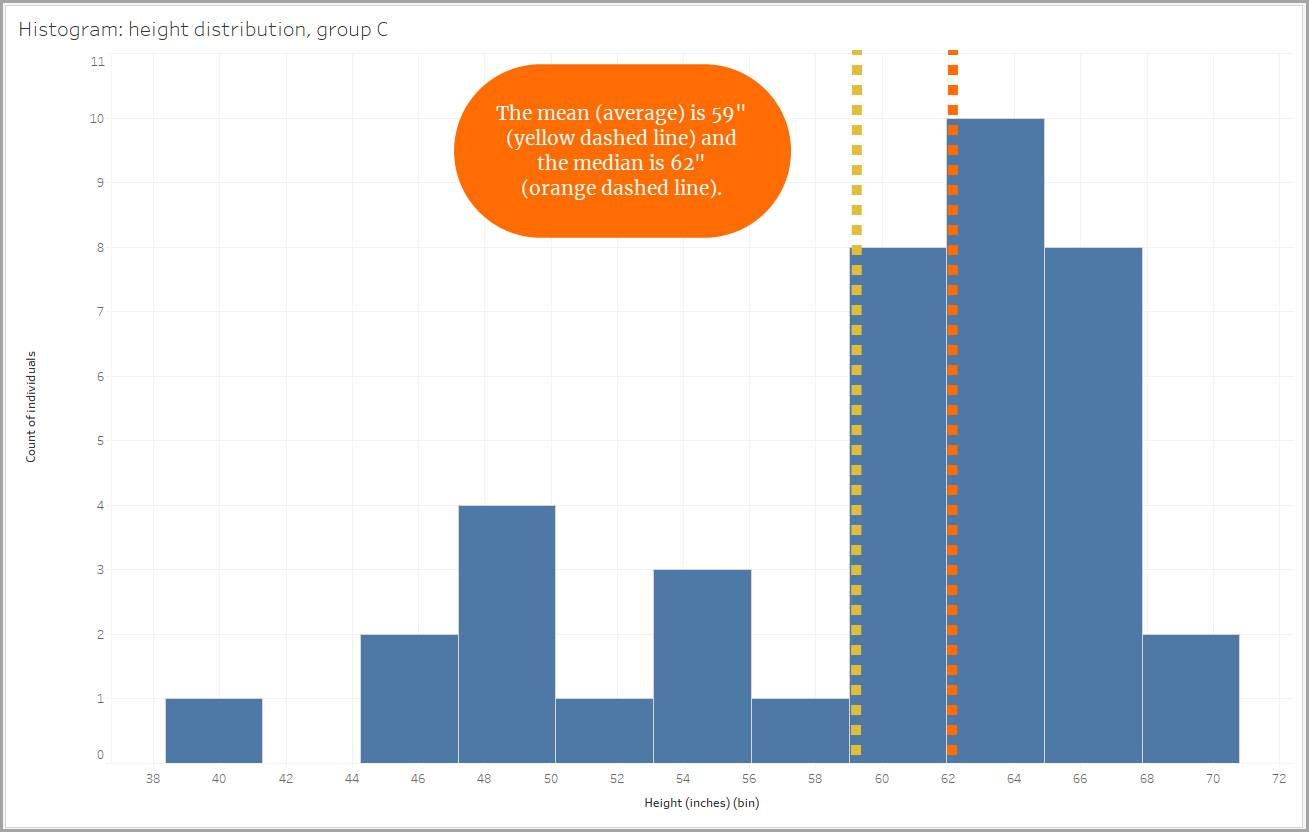
히스토그램
이 유닛에서 살펴본 모든 차트는 히스토그램입니다. 히스토그램은 가로 막대형 차트와 유사하게 보이지만 연속형 변수의 값을 동일한 크기의 범위 또는 빈으로 그룹화합니다.
이 히스토그램은 올림픽 선수에 대한 정보가 있는 데이터 집합을 사용합니다. 데이터 집합의 변수 중 하나는 18세에서 90세까지의 선수 연령을 포함합니다. 히스토그램을 통해 선수들이 어떻게 다른 연령대로 나뉘는지 볼 수 있습니다.
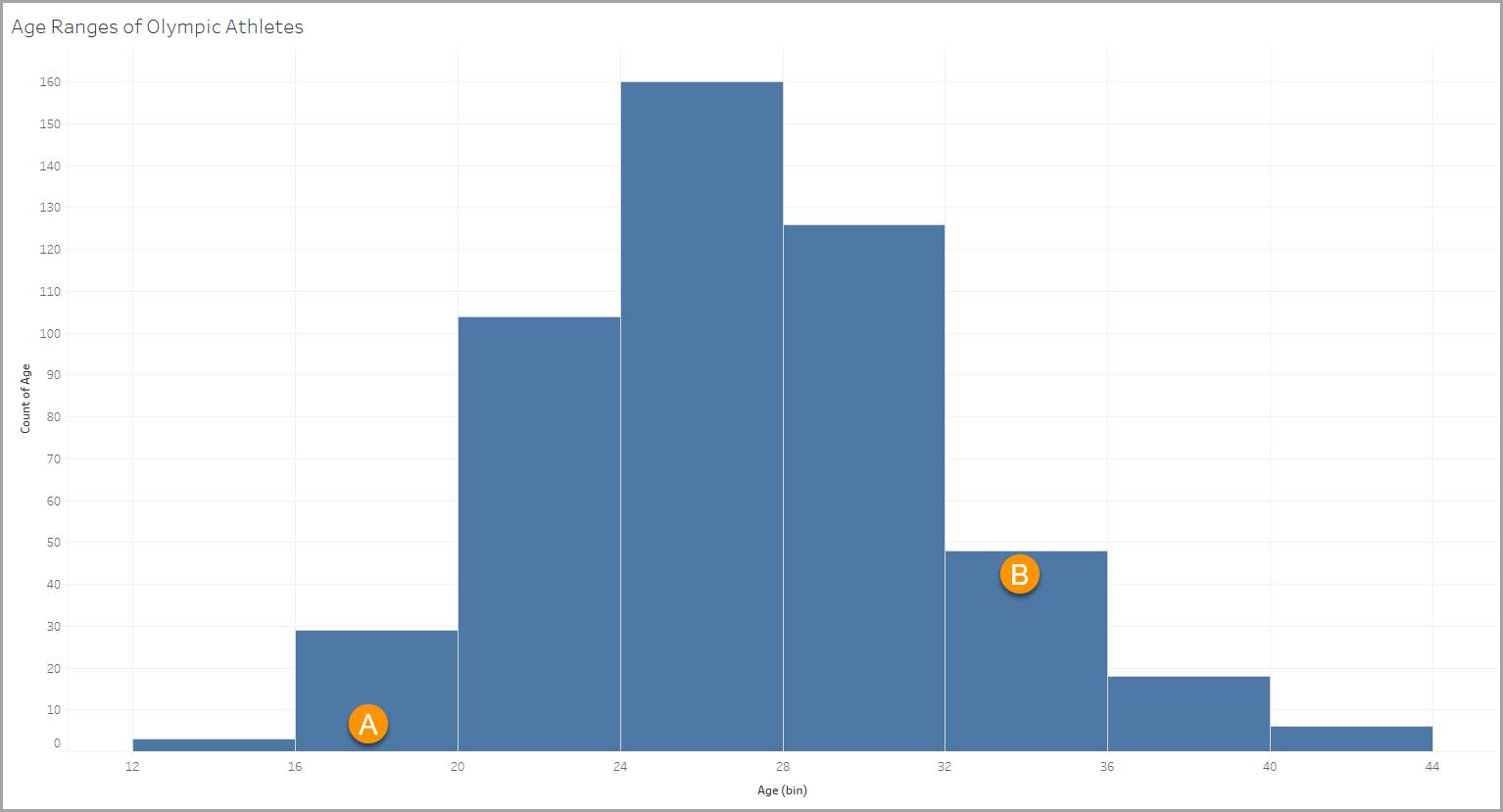
빈
각 빈은 12~15세, 16~19세(A), 20~23세, 24~27세 등 네 개의 연령 범위로 정의됩니다.
열
각 열은 빈의 기준을 충족하는 항목의 수를 나타냅니다(이 경우 연령 범위). 이 예에서는 32-35세 범위(B)에 있는 48명의 선수가 있습니다.
이제 히스토그램으로 구성된 연속 변수에 대한 분포를 살펴보았습니다. 다음 유닛에서는 상자 플롯을 사용하여 연속 변수의 분포를 보는 방법을 살펴보겠습니다.
리소스