상자 플롯을 사용하여 연속 변수 분포 표시
학습 목표
이 유닛을 완료하면 다음을 수행할 수 있습니다.
- 데이터 분포를 나타내기 위해 상자 플롯을 사용하는 방법을 설명할 수 있습니다.
- 상자 플롯을 만들 수 있습니다.
지금까지 변수 분포를 볼 수 있는 여러 가지 방법을 살펴보았습니다. 이 유닛에서는 상자 플롯이라고 하는 또 다른 중요한 그래프에 대해 알아봅니다. 1970년대에 미국의 수학자 John Tukey에 의해 소개된 상자 플롯은 시각적으로 간결한 데이터 분포를 보고 대조하는 방식입니다.
상자 플롯의 상자는 데이터의 중간 50%를 보여줍니다. 이 데이터는 25번째 백분위수에서 75번째 백분위수까지 확장되며 중앙값은 50번째 백분위수입니다.
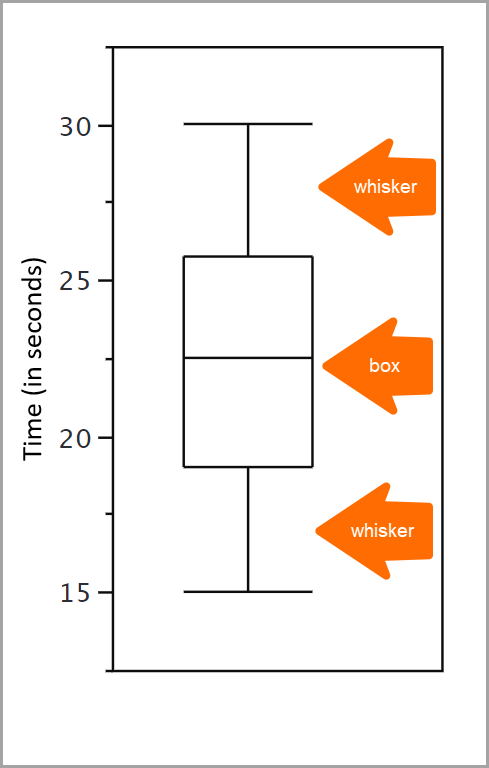
백분위수는 점수가 동일한 데이터 집합 내의 다른 점수와 비교되는 방식을 나타냅니다. 예를 들어, 내향성 수준을 측정하기 위해 퀴즈를 푸는 것입니다. 내향성 점수만으로는 해석하기가 어렵습니다. 자신의 점수가 다른 사람과 어떻게 비교되는지 확인하고, 수줍음 점수가 낮은 사람의 백분율을 알고자 합니다. 이 백분율은 백분위수입니다. 다른 시험 응시자의 65%가 여러분에 비해 덜 부끄러워하는 점수를 받은 경우 여러분의 점수는 65번째 백분위수입니다.
검토를 위해 상자 플롯의 상자는 데이터의 중간 50% 또는 25–75 백분위수를 보여줍니다. 하지만 그 바깥에 있는 데이터는 어떨까요? 여기에서 수염이 들어오고, 상자 외부에 플로팅되며 수염은 수평 스트로크로 끝나는 수직선입니다. 이상점을 포함하여 데이터(상자)의 중간 50%에 속하지 않는 가치에 대한 인사이트를 제공합니다. 이상점은 비정형 및 드문 관찰, 또는 분포의 중심으로부터 극단적인 편차를 갖는 값으로 이해될 수 있습니다.
이 모든 개념을 이후 유닛에서 더 자세히 살펴보겠습니다.
상자 플롯 만들기
다음 상자 플롯 예는 David M. Lane의 온라인 통계 교육: 멀티미디어 강좌 학습의 상자 플롯에 대한 챕터에서 각색되었습니다. 프로젝트 리더: 라이스 대학교의 David M. Lane
저자는 31명의 학생으로 구성된 수업 중 실험을 사용했습니다. 학생들에게 각각 30개의 색이 있는 직사각형이 주어진 페이지에서 가능한 한 빨리 색의 이름을 지정하는 것이 과제였습니다.
이들의 시간(초)은 다음 표에서와 같이 기록되었습니다.
|
14 |
17 |
18 |
19 |
20 |
21 |
|
15 |
17 |
18 |
19 |
20 |
22 |
|
16 |
17 |
18 |
19 |
20 |
23 |
|
16 |
17 |
18 |
20 |
20 |
24 |
|
17 |
18 |
18 |
20 |
21 |
24 |
| 29 |
이 데이터 집합을 사용하여 상자 플롯을 만들어 보겠습니다. 다음은 계정을 만드는 데 필요한 단계의 개요입니다.
- 백분위수를 계산합니다.
- 백분위수에 따라 상자를 표시합니다.
- 단계 크기를 결정합니다.
- 수염을 추가합니다.
- 외부 값을 추가합니다.
백분위수 계산
상자 플롯의 상자는 데이터의 25번째 백분위수에서 75번째 백분위수로 확장됩니다. 50번째 백분위수가 상자 안에 그려집니다. 상자 하단(하단 힌지라고 함)은 25번째 백분위수이고, 상자 상단(상단 힌지라고 함)은 75번째 백분위수입니다.
다음 단계에서는 수직선을 사용하여 백분위수를 살펴보겠습니다.
-
가장 작은 점수부터 가장 큰 점수까지 나열합니다.
-
중앙값 또는 중심값을 결정합니다. 중앙값은 숫자 연속열의 시작과 끝 사이에 표시됩니다. 31개의 값이 있는 연속열의 경우, 중간값은 중앙값 앞에 15개의 값이 있고 뒤에 15개의 값이 있다는 것을 의미합니다. 따라서 중앙값은 19입니다.
-
25번째 백분위수를 구합니다. 25번째 백분위수의 값은 연속열 시작과 중앙값 사이에 표시됩니다. 31개의 값의 예에서 이 중간 위치는 앞에 7개의 값과 중앙값 사이에 7개의 값이 있습니다. 따라서 25번째 백분위수의 값은 17입니다.
-
75번째 백분위수를 구합니다. 75번째 백분위수의 값은 중앙값과 연속열의 끝 사이의 중간에 표시됩니다. 31개 값의 목록의 경우, 이 중간 위치는 중간 위치와 중앙값 사이에 7개의 값, 그리고 중간 위치와 연속열의 끝 사이에 7개의 값을 가지고 있습니다. 따라서, 75번째 백분위수의 값은 20입니다.
백분위수에 따라 상자 플로팅
해당 값을 연결하고 상자를 플로팅해보겠습니다.
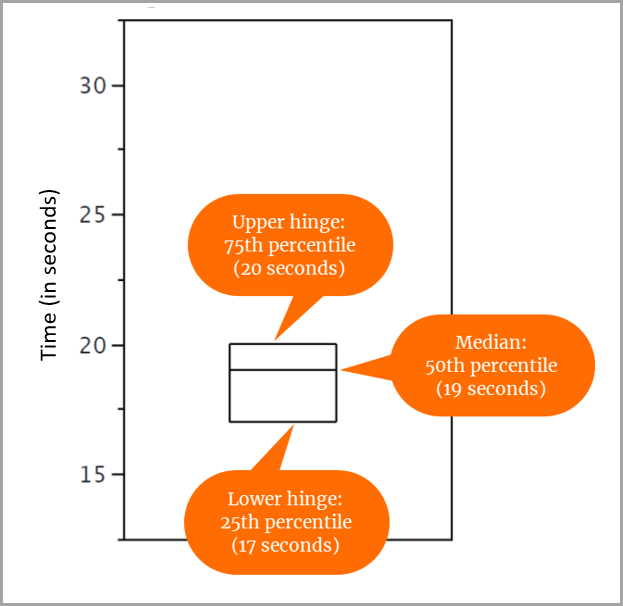
31개의 점수에 대해 다음과 같이 정했습니다.
- 25번째 백분위수는 17입니다.
- 50번째 백분위수(또는 중앙값)는 19입니다.
- 75번째 백분위수는 20입니다.
그래서 다음과 같이 상자를 그리게 됩니다.
- 25번째 백분위수(아래쪽 힌지)는 y축에서 17과 일치합니다.
- 50번째 백분위수(중앙값)는 y축의 19와 일치합니다.
- 75번째 백분위수(상부 힌지)는 y축에서 20과 일치합니다.
데이터 값의 중간 50%가 상자에 나타납니다.
참고: 25번째 백분위수에서 중앙값까지의 값을 두 번째 사분위수라고도 하며, 51번째 백분위수(중앙값 바로 다음)에서 75번째 백분위수까지의 값을 세 번째 사분위수라고 합니다. 25번째 백분위수보다 작은 값은 첫 번째 사분위수라고도 하며 75번째 백분위수보다 큰 값은 네 번째 사분위수라고도 합니다. 수염과 기타 표식을 사용하여 첫 번째 및 네 번째 사분위수 값을 표시합니다.
단계 크기 결정
이제 데이터 확산에 대한 추가 정보를 제공하기 위해 상자 위와 아래에 수염을 그릴 준비를 합니다. 수염 배치는 단계별로 결정되며, 여기서 단계는 1.5 x IQR로 정의됩니다. IQR은 사분위간 범위입니다.
복잡하게 들리겠지만, IQR은 단순히 상단 힌지 값(75번째 백분위수)과 하단 힌지 값(25번째 백분위수)의 차이를 의미합니다. 데이터 값의 중간 50%는 이 값으로 둘러싸인 상자에 있습니다.
점수 집합에서 상단 힌지의 값은 20이고, 하단 힌지의 값은 17입니다. 그래서 IQR은 20 빼기 17, 즉 3입니다.
단계 크기를 결정하려면 3(IQR)에 1.5를 곱하여 단계 크기로 4.5를 얻습니다.
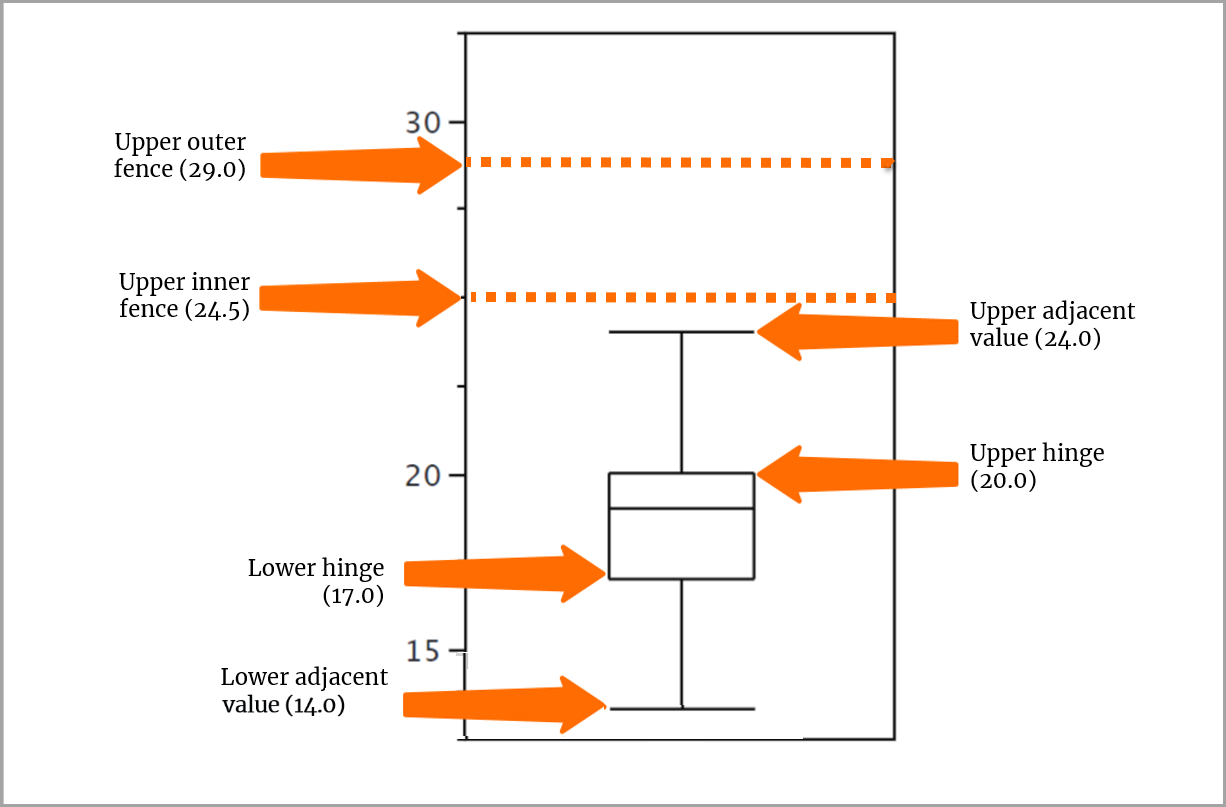
수염 추가
수염을 그리는 방법을 이해하려면 먼저 몇 가지 용어와 용어가 예제에서 점수에 어떻게 적용되는지 살펴보겠습니다.
수염은 어디로 가나요?
위쪽 힌지에서 위쪽 인접 값까지, 아래쪽 힌지에서 아래쪽 인접 값까지 수염을 그릴 수 있습니다.
수염은 외부 값까지 도달하지 못합니다. 대신, 작은 o로 외부 값을 나타내고, 별표(*)로 먼 바깥쪽 값을 나타냅니다.
점수 데이터에 대해 수염은 상단 힌지 값(20)으로부터 상단 인접 값(24)까지 및 하단 힌지 값(17)으로부터 하단 인접 값(14)까지 연장됩니다.
외부 값 추가
내부 울타리 너머의 값이지만 외부 울타리 너머 값은 아닌 것이 외부 값입니다. 이 값 중 하나인 29를 점수 집합에 가지고 있습니다. 즉 외부 울타리의 값과 일치하지만 이 값을 넘지는 않습니다. 이 값을 나타내는 데 작은 o를 사용합니다.
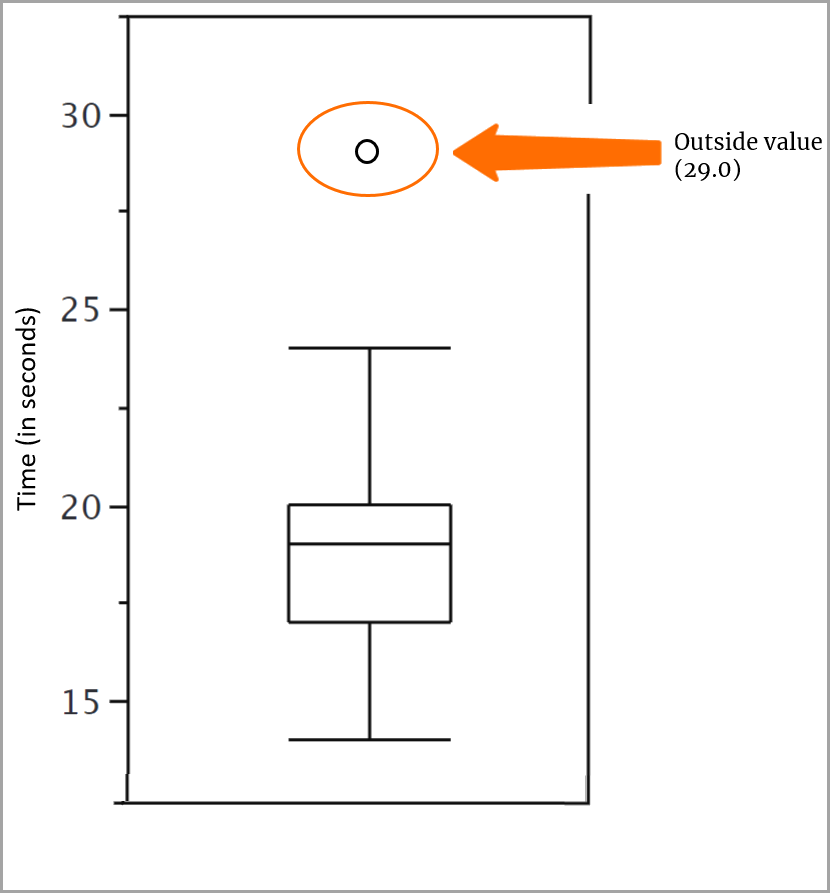
그리고 그것으로, 상자 플롯은 완성되었습니다!
상자 플롯과 히스토그램 비교
상자 플롯이 분포를 나타내는 히스토그램과 어떻게 다른지 궁금할 수 있습니다.
- 히스토그램은 빈을 사용하여 값의 빈도를 플로팅합니다.
- 상자 플롯에서 데이터의 중간 50%가 상자에 나타나고 이상점(존재하는 경우)이 수염 외부에 플로팅됩니다.
어떻게 표시되는지 알아보려면 사람들의 높이 분포의 모양을 보여주는 데이터로 돌아갑니다. 데이터가 히스토그램과 상자 플롯에 표시되는 방식을 비교합니다.
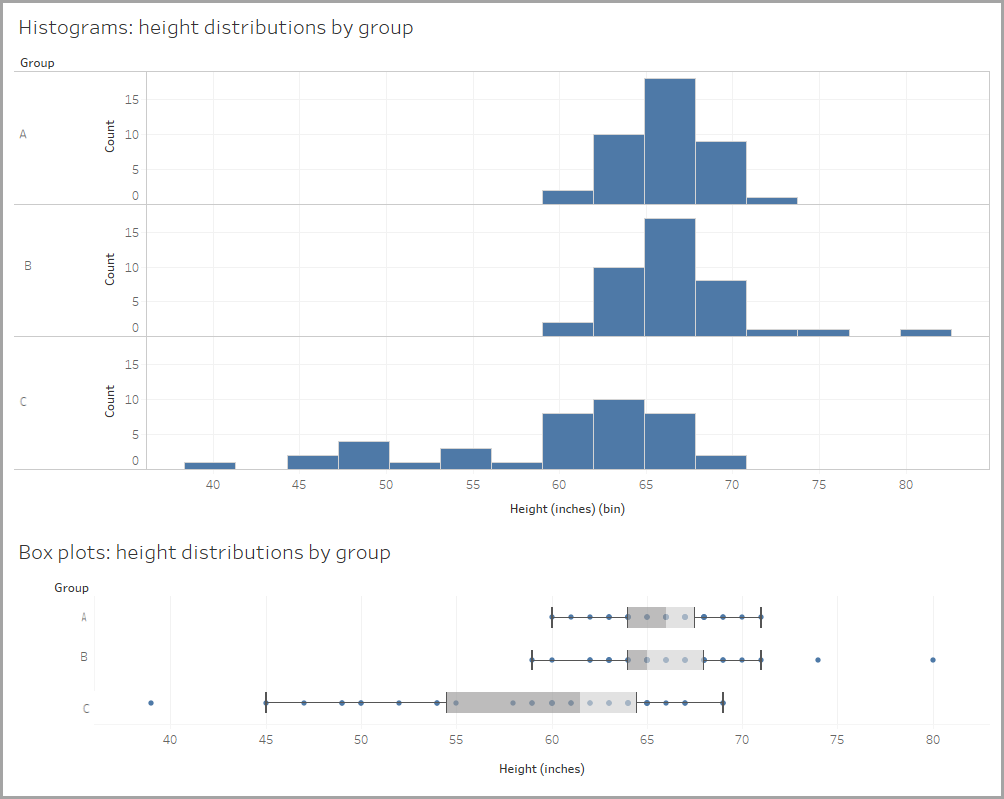
상자 플롯이 얼마나 적은 공간을 사용하는지 주목하세요. 이렇게 하면 분포를 쉽게 비교할 수 있습니다. 3개의 병렬 분포는 히스토그램보다 상자 플롯과 비교하기 쉽습니다. 몇 가지 예를 더 살펴보겠습니다.
이제 데이터 탐색, 이해 및 소통을 위해 배포판이 어떻게 도움이 되는지 이해할 수 있습니다.