ヒストグラムを使用して連続変数の分布を表示する

学習の目的

この単元を完了すると、次のことができるようになります。

• 連続変数の分布の形状を認識する。
• ヒストグラムを使用してデータの分布を表す方法を説明する。

前の単元では、離散変数 (キャンディの色) の分布について確認し、離散変数は値がそれぞれ分離しているのに対して、連続変数は値が切れ目なく全体を形成していることを学習しました。この単元では、連続変数の分布とヒストグラムを使用してその分布を表す方法について説明します。

次の例は、『Online Statistics Education: An Interactive Multimedia Course of Study (オンライン統計学教育: インタラクティブマルチメディア学習指導要領)』(プロジェクトリーダー: David M. Lane 氏 (ライス大学)) の箱ヒゲ図に関する章から引用したものです。

20 回の試行で、著者の 1 人がカーソルをターゲット上に移動させる際の応答時間を記録しました。「応答時間」という変数は連続的であり、時間をミリ秒単位で測定すると、それぞれの応答時間が同じになることはありませんでした。

次の表は、各応答時間をミリ秒単位で表したものです。

応答時間をグループ化した度数分布

前の単元で度数分布について学んだことを振り返ってみましょう。 上の表の応答時間の値を度数分布で表すと、20 個の異なる値があり、それぞれの頻度は 1 になります。これでは、あまり役に立ちません。 

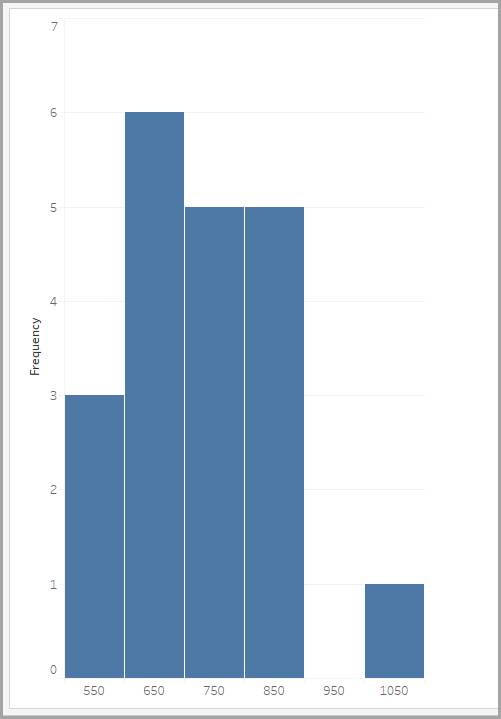
この問題を解決するには、グループ化された度数分布を作成し、次のように、同じサイズのさまざまなビン (値の範囲) に応答時間が収まるような表を作ります。

ヒストグラムを使用すると、グループ化された度数分布をグラフィカルに表示することができます。X 軸上のラベルは、それぞれのビンが表す中央値です。 

ヒストグラムについては、後で詳しく説明します。まず、さまざまな分布の形状と、その形状からヒストグラムのデータについて何がわかるかを見ていきましょう。

分布の形状

分布にはさまざまな形状があります。分布は、中央から左右に値が均等に分布する対称形になることがあります。また、右側に多くの値が広がって正の方向に歪んでいる場合や、左側に多くの値が広がって負の方向に歪んでいる場合もあります。

3 つの異なるグループの人たちの身長を測定したとします。身長の分布を示すために、グループごとにヒストグラムを作成します。

ビンのサイズは 2.95 インチで、グループの人たちの身長は 59 ～ 61.95 インチ、62 ～ 64.95 インチのようにビンに分けられています(このビンのサイズは Tableau Desktop で自動的に作成されました)。

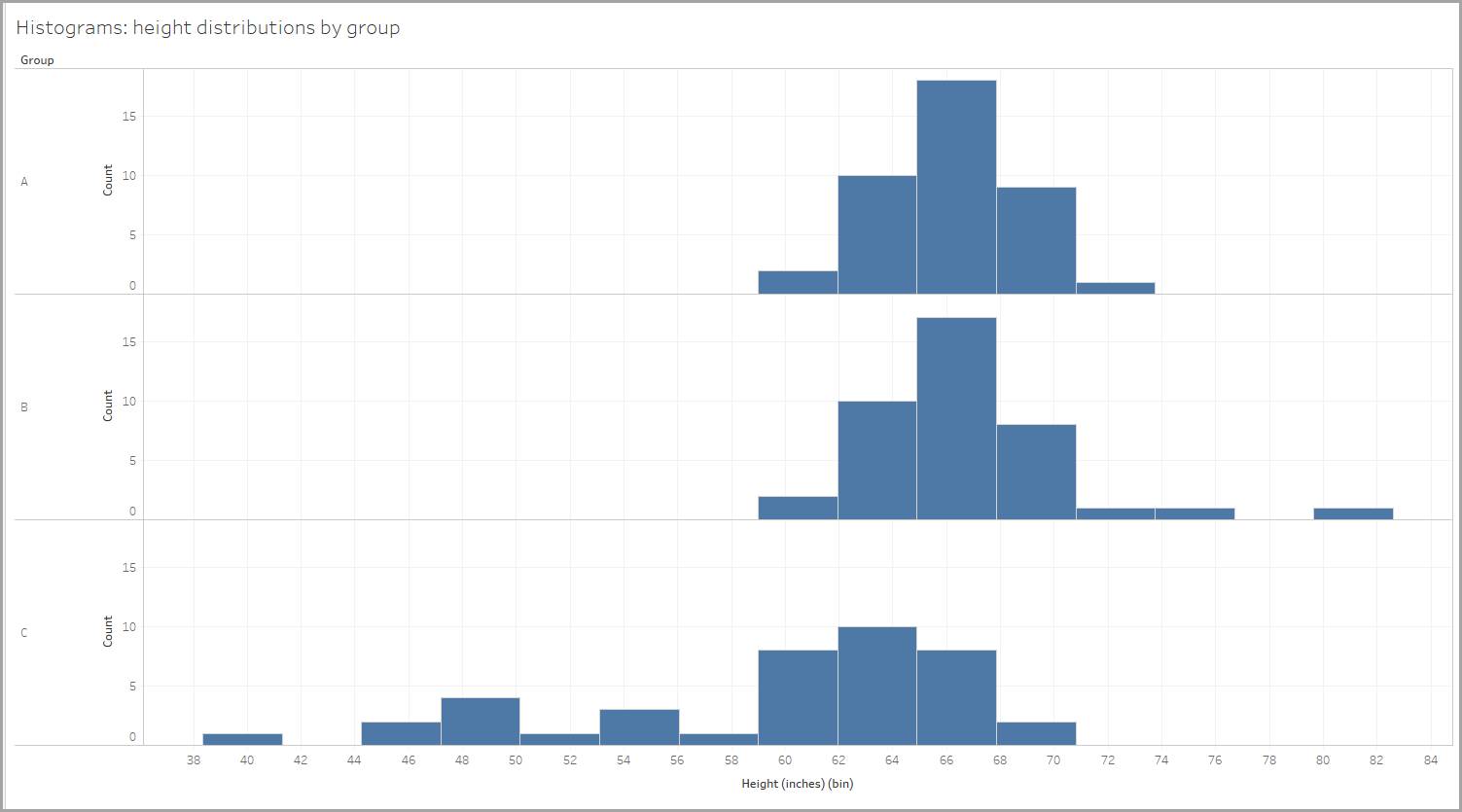
それぞれの分布の形状について見ていきましょう。次に示すように、それぞれの分布では、平均値と中央値 (データポイントの真ん中の値) によって形状が異なっていることがわかります。 

対称分布

この例では、あるグループの身長分布がほぼ対称になっています。これを半分に折れば、2 つの面はほぼぴったり重なります。

完全に対称な分布では、データの中心は平均値と中央値 (データポイントの真ん中の値) の両方になります。この 2 つの値は等しいためです。データの中心は両方の値で表され、データの広がりは中央から左右に同じだけ広がっています。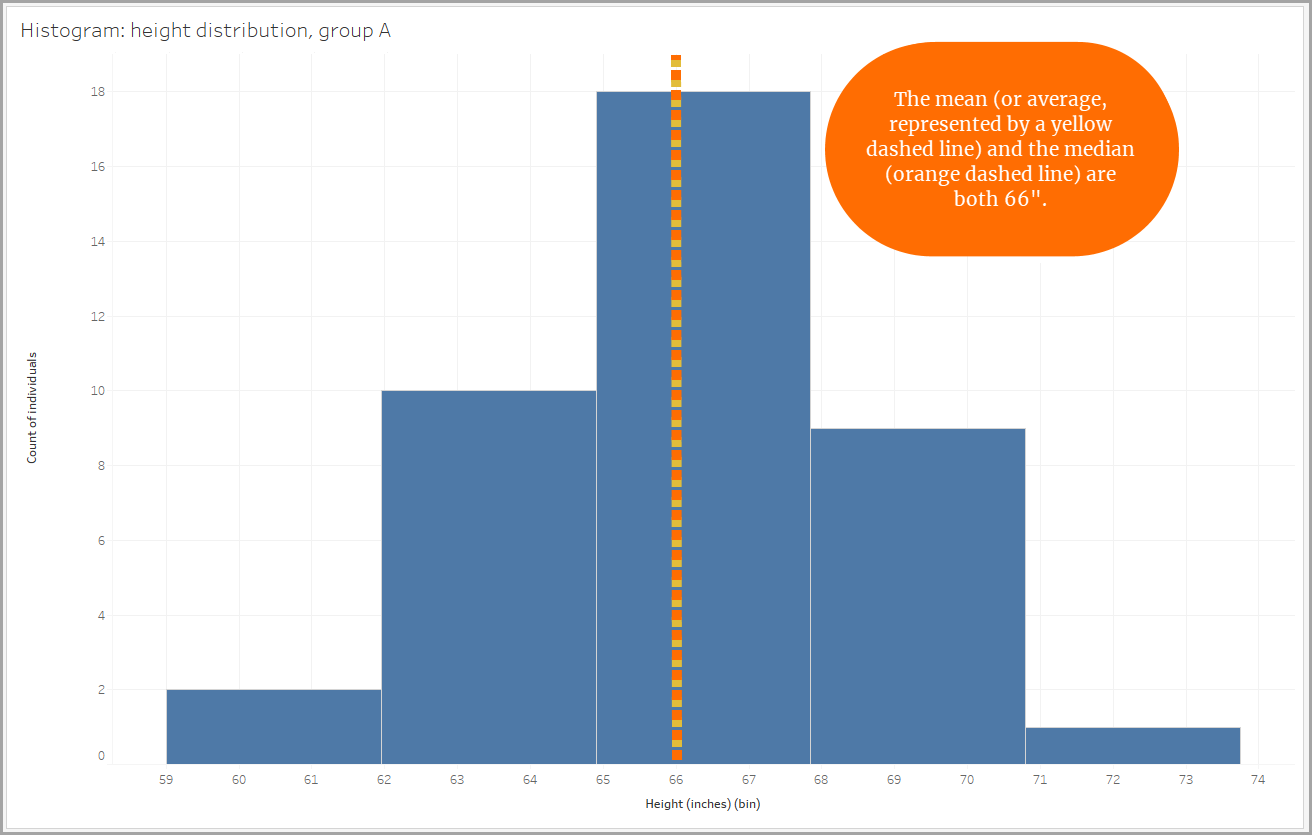

正の歪みのある分布

非対称の分布もあります。ある分布のデータが、負の方向よりも正の方向へ大きく広がっている場合、それは正の歪みのある分布です。正の歪みは、データが右に伸びるため、右方向の歪みとも呼ばれ、右側の「裾」の方が長くなっています。分布が正に歪んでいる場合、中央値は平均値よりも小さくなります。

たとえば、億万長者が何人か居住している都市があるとします。億万長者の高い所得によって、都市の平均所得には歪みが生じ、平均所得が実際よりも高く見えることになります。この都市の全住民の経済状態を正しく反映するには、中央値の方が適しているでしょう。

同様に、身長のデータを見ると、1 つのグループは約 72 インチ (6 フィート) 以上の人が 3 人がいるために、正の歪みが見られます。この 3 人の高い身長によって、平均値が高くなっています。そのため、この場合もグループの身長を把握するには、中央値を使用する方が適切です。

負の歪みのある分布

もう 1 つの非対称な分布は、負の歪みのある分布です。負の歪みのある分布のデータは、正の方向よりも負の方向に大きく広がっています。負の歪みは、データが左に伸びるため、左方向の歪みとも呼ばれ、左側の「裾」の方が長くなっています。分布が負に歪んでいる場合、中央値は平均値よりも大きくなります。

たとえば、20 人の生徒がいるクラスについて考えます。このクラスには、一度も授業に出席せず、課題もこなしていない生徒が 2 名います。この 2 人の生徒の最終成績は 0.0 でした。この 0.0 という成績により、クラスの成績を平均した結果に歪みが生じ、生徒の平均成績が実際よりも低く見えることになります。このクラスの生徒の成績を正しく反映するには、中央値の方が適しています。

同様に、身長のデータを見ると、1 つのグループは 60 インチ (5 フィート) 未満の人がいるために、負の歪みが見られます。この人たちの低い身長によって、平均値が低くなっています。

ヒストグラム

この単元で確認したすべてのグラフはヒストグラムです。ヒストグラムは、棒グラフのように見えますが、連続変数の値が同じサイズの範囲 (ビン) でグループ化されています。 

次のヒストグラムは、オリンピック選手に関する情報のデータセットを使用しています。データセット内の変数の 1 つには、選手の年齢が含まれています。このヒストグラムでは、選手の年齢の内訳を確認することができます。

ビン

各ビンは、12 ～ 15 歳、16 ～ 19 歳 (A)、20 ～ 23 歳、24 ～ 27 歳のように、4 歳刻みで定義されています。 

棒

それぞれの棒は、ビンの条件を満たす項目の数を表します (このケースでは年齢層)。この例では、32 ～ 35 歳の年齢層 (B) の選手が 48 人います。

ここでは、ヒストグラムとして整理された連続変数の分布について学習しました。次の単元では、箱ヒゲ図を使った連続変数の分布の表示について学習します。

リソース

• Web サイト: David M. Lane 氏によるパブリックドメイン著作物、Introduction to Statistics (統計学入門)
• Tableau ヘルプ: Build a Histogram (ヒストグラムの作成)