データの相関を検証する
学習の目的
この単元を完了すると、次のことができるようになります。
- 相関を定義する。
- 強い相関関係と弱い相関関係を区別する。
データの有効活用を目指したジャーニー
データリテラシーは、データの使用やデータによる情報の伝達を容易に行うための基盤です。
「データリテラシーの基本」モジュールでは、毎日のテレビの視聴時間数、マイル単位で測定された時速、インチで計測したある都市での年間総雨量、ドルでの売上高、マーケティングに費やした金額など、量的変数を数値で測定できる特性として説明しています。
データ内の関係性を調べるとき、売上とマーケティングに費やした金額のような 2 つの変数がどの程度密接に関連しているかをどのように判断するのでしょうか? また、一方の変数から他方の変数を予測することができるでしょうか?
相関と回帰は、トレンドを把握し、予測を行うために使用される重要な技法です。分析で使用される重要な形式は他にもありますが、ここでは AI と分析で使用される最も単純な形式である線形の相関と回帰を中心に説明していきます。
この単元では、相関の概念について理解します。相関とは、2 つの変数が相互に関連して移動しているかどうか、およびどの程度密接に移動しているのかを説明するものです。相関関係によって、どのように関連性が測定されるのかについて、ただし因果関係は証明されないことについて、理解できるようになります。次の単元では、線形回帰を使用してある変数の値を別の変数に基づいて計算または予測する方法と、このモデルがデータにどの程度適合するかを測定する方法についても説明します。
相関とは?
相関とは、2 つの量的変数 (数量を表す変数) の間に関連性があるかどうか、およびその関連性の強さを示す技法です。
この単元では、ピアソンの相関について説明します。その他にも非線形相関がありますが、ここでは取り上げません。
たとえば、1 日の消費カロリーと体重の間には関係があるでしょうか? 消費カロリーが多い人ほど体重が多いでしょうか? 相関では、こういった人たちの体重と摂取カロリーとの間にどの程度強い関連があるかが示されます。
体重と摂取カロリーの間の相関は簡単な例ですが、皆さんが扱うデータの中には期待通りの関係がないものもあります。また、複数の相関があることが予想されるものの、どの相関が強いのかわからない場合もあります。相関分析は、データを理解するうえで役立ちます。相関性分析は、データを理解するうえで役立ちます。
相関性分析を開始する場合は、散布図を作成すると、2 つの量的変数間の関係を調べることができます。変数はデカルト座標としてプロットされ、データポイントごとに水平方向の X 軸上でどの位置にあるか、垂直方向の Y 軸上でどの位置にあるかがマークされます。以下の散布図には、売上高とマーケティングに費やした金額の関係が示されています。一方の変数が増えると、もう一方も増えているように見えるという、相関があるようです。
この単元内の概念は、David M. Lane 氏によるオンラインのパブリックドメイン著作物『Introduction to Statistics (統計学入門)』から引用したものです。
相関関係 vs. 因果関係
相関がどのように定義され、どのようにグラフで表現されるかを把握できたところで、相関をより深く理解する方法について説明しましょう。
まず知っておくべき重要な点は、相関は決して因果関係を証明するものではないということです。
ピアソンの相関は、単に 2 つの量的変数間の線形的な関連がどの程度強いかを表すだけです。どのように関連しているか、またなぜ関連しているかは表しません。
たとえば、エアコンの売上と日焼け止めの売上は互いに相関します。人々は、日焼け止めを買ったという理由でエアコンは買いませんし、その逆でもありません。両方を買った理由は「暑さ」だからです。
どのように相関を測定するのか?
ピアソンの相関 (相関係数ともいう) は、2 つの量的変数間の線形関係の強さと方向 (正または負) を測るために使用されます。データのサンプルで相関を測定する場合、記号として r が使われますピアソンの r の範囲は -1 ～ 1 です。
r = 1 の場合、変数間には完全な正の線形関係があります。つまり、一方の変数の値が増えるにつれて、もう一方もそれに完全に相関して増えていきます。r = -1 の場合、変数間には完全な負の線形関係があります。完全な負の相関では、一方の変数の値が増えるにつれて、もう一方が同じ分だけ減っていきます。 r = 0 の場合、変数間には線形関係がありません。
実際のデータでは、r の値が -1、0、1 になることはありません。
一般的には、以下の表に示すように、r が 1 または -1 に近づくほど相関性が強くなります。
| r = | 相関 |
|---|---|
|
0.90 ～ 1 または -0.90 ～ -1 |
非常に強い相関 |
|
0.70 ～ 0.89 または -0.70 ～ -0.89 |
強い相関 |
|
0.40 ～ 0.69 または -0.40 ～ -0.69 |
中程度の相関 |
|
0.20 ～ 0.39 または -0.20 ～ -0.39 |
弱い相関 |
|
0 ～ 0.19 または 0 ～ -0.19 |
非常に弱い相関または相関なし |
このトピックに関するリソースの中には、相関の強さを単に、強い、中程度、弱いとだけ分類しているものもあります。
線形相関の条件
意味のある相関になるための条件として、量的変数が使用されること、線形関係を表すこと、外れ値の影響が考慮されることなどを検討する必要があります。相関性分析を実行する前に、必ずこのような条件を確認してください。
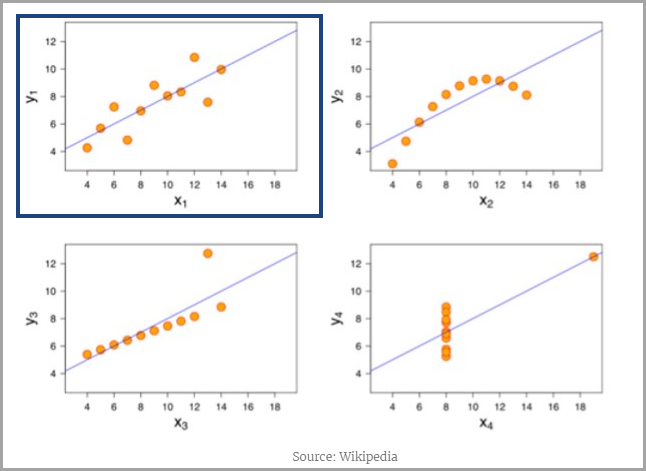
1973 年、統計学者の Francis Anscombe 氏は「アンスコムの数値例」を用いて、統計的検定のみを行うだけでなくデータを視覚的にグラフに描くことの重要性を示しました。4 つのビジュアライゼーションはすべて同じ傾向線方程式を示しています。この数値例を見ると、ビジュアライゼーションがなぜそれほど重要なのかがわかります。つまり、統計的検定ではわかりにくいデータ内の傾向を特定することができます。
以下の例では、4 つのうち左上の散布図だけが、外れ値のない線形であるという条件を満たしています。右上の散布図は線形関係を示しておらず、非線形モデルがより適切です。下の 2 つの各散布図には、結果に大きな影響を与えかねない外れ値が含まれています。
これで、相関という統計手法の概念の理解を深めることができました。次の単元に進んで、線形回帰について学びましょう。