Skip to main content

Make Inferences

Learning Objectives

After completing this unit, you’ll be able to:

  • Describe the purpose of hypothesis testing.
  • Define the use and limitations of p-values in hypothesis testing.

Introduction

In the previous unit, you encountered concepts around using variation and the normal distribution to explore, interpret, and communicate with data. You also looked at confidence intervals as an example of inference.

In this unit, you continue to learn about inference. Inference is the process of drawing conclusions about a population based on a sample of the data. It’s useful because, in most instances, it’s not practical to obtain all the measurements in a given population.

In other words, if we have data for all the members of a population, we don’t need to make any inferences about the difference between groups within that population. When it isn’t possible to gather data for every individual member of a population, we collect data from samples, and then make inferences.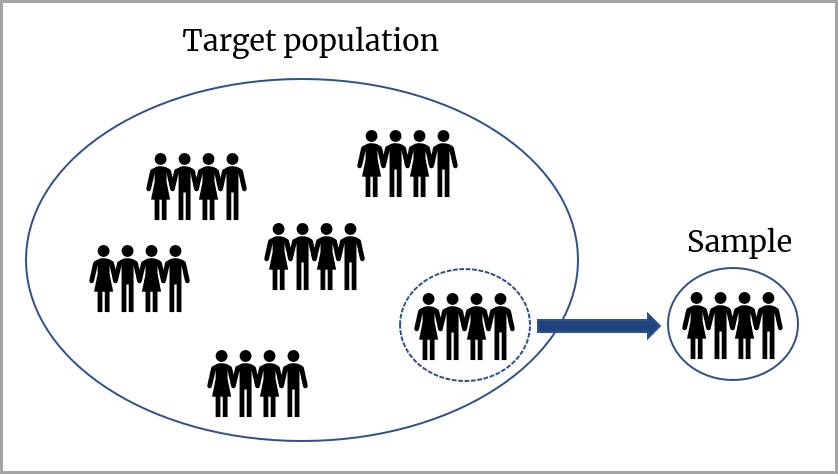Cartoon people in a large oval that represents the total population and a smaller number of cartoon people in a smaller oval that represents the sample

In his book Avoiding Data Pitfalls, author Ben Jones, founder and CEO of Data Literacy, LLC, and a member of the Tableau Community, points out that the census in the United States happens only once a decade due to how expensive and complicated it is to try counting “every single person in every single residential structure in the entire country and such an undertaking is not without its sources of bias and error.” Because most organizations do not have financial or human resources that equal the US federal government’s, they base decisions on inferences made from looking at data samples.

Hypothesis Testing

Many types of organizations use hypothesis testing. Some businesses, for example, use hypothesis testing for quality control to see if a certain product meets a standard or to compare new and old sales methods.

Medical research also often bases inferences on data samples. Imagine that a biotech company manufactures a new drug to alleviate a disease. To determine whether the medication works, a controlled experiment needs to be conducted. Because it isn’t possible to experiment on every person who has the disease, a subset of people with the disease are randomly sampled for testing.

A flow chart with colored rectangles to show that random assignments divide groups and each group has effects measured

Within this sample, the experimental group receives the treatment, and the control group receives a placebo instead of the medication. The groups are randomly assigned so that any difference in health outcomes can be attributed to research intervention. 

Tests are set up for both groups and measurements are taken. When testing differences between the two groups, researchers decide how far apart the results must be in order to determine if the health outcomes for the experimental group and the control group are significantly different.

Researchers collect data from the sample groups and run appropriate statistical tests. Then, the researchers use these test results to decide if there is a significant difference in the groups. Once the data has been obtained, the researchers will need to make inferences about the population at large, meaning every single person who has the disease. This is called hypothesis testing.

Hypothesis testing begins with the creation of null and alternative hypothesis statements.

  • Null hypothesis states that the medication will have no impact on health outcomes. It proposes that those who receive the treatment will not have different outcomes from those who do not.
  • Alternative hypothesis states that there will be a difference in health outcomes. It proposes that those receiving the medication will show more improved health outcomes than those who do not.

Hypothesis tests begin by assuming that the null hypothesis is true. The tests then aim to discern how likely it is to observe outcomes that are at least as great as in the experiment, assuming the null is true. 

In other words, if it’s a small probability that the results would be as great if the null is true, then there is evidence to support the alternative hypothesis. If it’s a large probability that the results would be as great if the null is true, then there is not enough evidence to support the alternative hypothesis, and researchers should try again with a new formula. 

Hypothesis tests take the number of samples, the size of the difference measured, and the amount of variation observed in each group into account.

The numeric result of a hypothesis test (the probability that the null hypothesis is true) is called the p-value. A p-value helps determine whether to reject the null hypothesis. In this case, rejecting the null hypothesis means that treatment would work in the larger population. A small p-value indicates that there is enough evidence to reject the null hypothesis and to support the alternative hypothesis.

It's important to note, however, that the p-value doesn't prove or disprove anything. A high p-value doesn’t prove that the null hypothesis is valid, and a low p-value doesn’t prove that it’s invalid. That’s why p-values need to be considered with care.

How to Use the p-Values

At one time, researchers were trained to use the p-value of 0.05 as a cut off. In other words, a p-value of 0.05 or lower was believed to be sufficient to reject the null hypothesis. The 0.05 cutoff corresponds to the tails of the normal distribution. Remember, 95% confidence intervals matched the area of the normal distribution that falls within -2 or +2 standard deviations from the mean. The 0.05 (or 5%) cutoff corresponds to the area that falls outside of -2 or +2 standard deviations from the mean.

That thinking has been revised over the past several years. In the medication experiment, if a lower cutoff was used (effectively raising the confidence interval above 95%), it could be harder to reject the null hypothesis. 

For these reasons, and many others, the American Statistical Association issued a statement in 2016 in which they claimed, “By itself, a p-value does not provide a good measure regarding a model or hypothesis.” 

P-values can also be manipulated by the kind of data brought into the analysis. 

To see an example of how p-values can be manipulated, take a look at this interactive “p-hacking” exercise, Hack Your Way to Scientific Glory, on FiveThirtyEight, a polling aggregation website that also analyzes opinion polls, politics, economics, and sports. 

You’ve now been introduced to inference, hypothesis testing, and p-values. Understanding these concepts can help you measure, describe, summarize, make comparisons in, and draw informed conclusions from your data.

Resources

Continua a imparare gratuitamente!
Registra un account per continuare.
Registrati Accedi
Cosa troverai?
  • Ottieni consigli personalizzati per i tuoi obiettivi di carriera
  • Metti in pratica le tue competenze con sfide pratiche e quiz
  • Monitora e condividi i tuoi progressi con i datori di lavoro
  • Accedi a risorse di tutoraggio e opportunità di carriera
Salta per ora