Lea los gráficos con confianza

Objetivos de aprendizaje

Después de completar esta unidad, podrá:

• Evaluar críticamente las interpretaciones de los datos.
• Usar una lista de verificación para evaluar la credibilidad y precisión de los gráficos.

La importancia de las interpretaciones cuidadosas

Incluso los gráficos creados con datos de fuentes precisas y opciones de diseño adecuadas están sujetos a malas interpretaciones. La clave es pensar críticamente y tomarse el tiempo para evaluar cuidadosamente las interpretaciones de los datos que ve representados en los gráficos y otras visualizaciones de datos.

Cuando lea un gráfico, tómese un momento para considerar si falta alguna información crítica. Si puede profundizar en los datos de la fuente, a veces encontrará información relevante que no se refleja en el gráfico. La información oculta o faltante puede sesgar la forma en que percibe los datos que se le presentan, independientemente de si las omisiones fueron intencionales. 

Considere las comparaciones hechas

“Las visualizaciones, si son para ayudar a pensar, deben mostrar comparaciones” (Edward Tufte, La belleza de la evidencia).

Como aprendió en la primera unidad, los gráficos pueden ayudarlo a tomar mejores decisiones. Lo ayudan a hacer comparaciones informadas y responden las preguntas correctas para ayudarlo a tomar buenas decisiones. Más allá de determinar la credibilidad de los datos de un gráfico, también es importante considerar el contexto del gráfico y comprender las comparaciones que se realizan. Incluso si los datos de un gráfico son confiables, es posible que llegue a conclusiones incorrectas si no se detiene para asegurarse de que el gráfico esté abordando, en primer lugar, las preguntas correctas. 

Piense en el panorama general

Otro escollo común para tener en cuenta es cuando los gráficos no muestran todo el contexto en un escenario. 

Por ejemplo, en “Cómo mienten los gráficos”, Alberto Cairo analiza el siguiente gráfico de barras. La conclusión sugerida es que la tasa de desempleo está aumentando. 

Sin embargo, si observa estos dos puntos de datos en el contexto de todo el año o incluso a lo largo de varios años, surge un patrón diferente. Aunque la tasa de desempleo aumentó entre julio de 2017 y agosto de 2017, la tasa en realidad está disminuyendo en el tiempo con fluctuaciones que ocurren entre meses. Esto cuenta una historia muy diferente.

Considere el margen de error y la incertidumbre 

Nada es perfecto, incluidos los datos. A veces, puede sorprenderse por los resultados de las elecciones cuando las encuestas muestran al candidato no ganador con una ventaja.

Al interpretar las encuestas, busque el margen de error o el intervalo de confianza. En este ejemplo, el margen de error fue de +/- 3 puntos porcentuales. ¿Qué significa esto?

El margen de error no describe “errores” en el estudio, sino que nos dice cuánta incertidumbre hay en nuestra estimación. Por lo general, una estimación es un punto medio de un rango. Imagínese tratando de medir la longitud de un perro muy inquieto y feliz. Cuantas más veces intente medirlo, más seguro estará de saber cuán largo es realmente. Sin embargo, todo lo que puede decir con certeza es que este perro en particular mide aproximadamente 71 cm de largo. 

En este ejemplo, diría: “Dados nuestros métodos de recopilación y medición, estamos un 95 % seguros de que el valor que estamos tratando de estimar está entre 42 y 48, o 3 puntos más o menos que 45, y de que el valor de Conor Lamb está entre 39 y 45, o 3 puntos más o menos que 42”.

Cuando los estadísticos describen el margen de error, lo dirán en un nivel de confianza o nivel de incertidumbre particular. Las estadísticas le permiten estar seguro de que, si ejecuta el estudio muchas veces con los mismos métodos, el 95 % de las veces su estimación caerá dentro del margen de error. En este ejemplo, las áreas de gradiente que representan el intervalo de confianza de +/- 3 puntos alrededor de las estimaciones de puntos se superponen, por lo que no podemos concluir que ninguno de los candidatos ganaría a partir de estos resultados. Además, si tenemos en cuenta el 13 % de los votantes indecisos en la encuesta, no es de extrañar que ninguno de los dos candidatos ganara la carrera.

Si revisa la encuesta y considera el margen de error, descubrirá que el resultado final estuvo dentro del margen de error. Un margen de error es el grado de incertidumbre que puede haber en el conjunto de datos. 

Por ejemplo, una encuesta podría indicar que el 60 % de los encuestados prefieren la marca A antes que la marca B. Si el margen de error es del 2 %, el porcentaje real de encuestados que prefieren la marca A está dentro del rango del 58 % al 62 %. 

Muchas fuentes citan el margen de error que se calculó para el conjunto de datos. Si el margen de error no está claramente establecido, tenga en cuenta que siempre hay un grado de incertidumbre que se debe considerar. 

Para ver el margen de error y la incertidumbre más detalladamente, consulte el módulo Comparaciones de las variaciones de datos.

La correlación no implica causalidad

La correlación solo muestra qué tan fuertemente están relacionadas las variables. No explica el cómo ni el por qué. 

Por ejemplo, las ventas de helados se correlacionan con la cantidad de anteojos de sol vendidos. ¿La gente compra helado porque compró anteojos de sol? ¿O viceversa? No. La causa de ambas compras es claramente otra. En este caso, la causa puede ser el clima cálido.

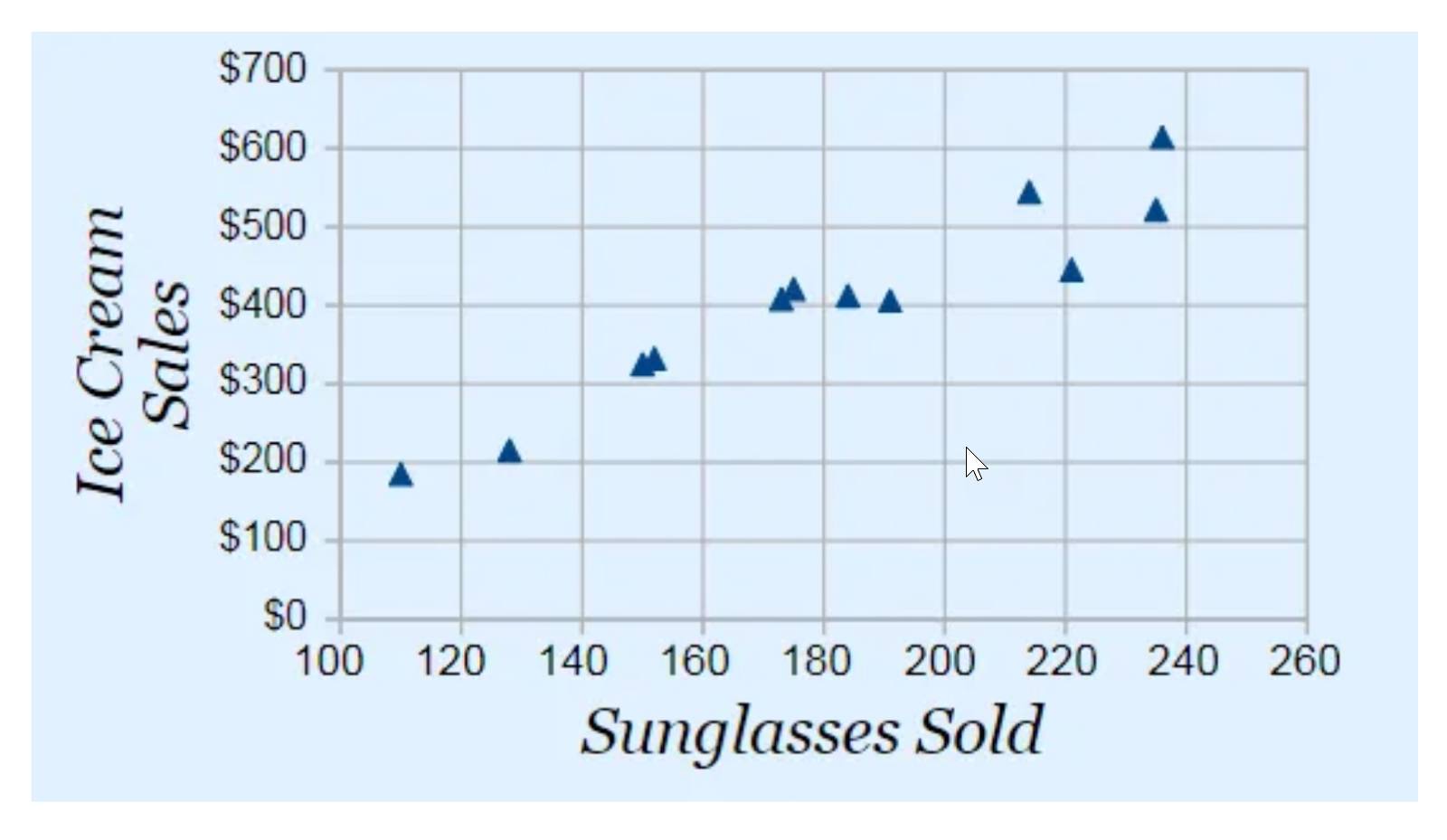
Es importante tratar de evitar hacer suposiciones y sacar conclusiones incorrectas basadas únicamente en la correlación. Considere siempre si puede haber otras variables ocultas que afecten lo que se muestra en los datos. 

Preste atención a las palabras

Tenga en cuenta el lenguaje usado para describir y anotar un gráfico. Tenga en cuenta lo siguiente:

• ¿El título y los subtítulos describen correctamente el gráfico?
• ¿El gráfico está correctamente etiquetado?
• ¿Las palabras tienen una carga emocional que influye en su percepción de los datos?

Siga haciendo preguntas

Cuando lea un gráfico y las interpretaciones o representaciones visuales de datos de otra persona, siempre haga preguntas. Si ve algo que no cuadra, pregunte por qué y profundice en los datos. Se sorprenderá lo que puede aprender y cómo puede ayudar a los que lo rodean manteniéndose curioso y haciendo preguntas inteligentes.

Lista de comprobación de SCAM

Para ayudar a guiar su revisión y análisis cuidadoso de los gráficos, consulte la lista de comprobación práctica de SCAM. SCAM significa Sources (fuentes), Charts (gráficos), Axes (ejes) y Messages (mensajes).

Lista de comprobación de SCAM

Use la lista de comprobación como un recordatorio para hacer las siguientes preguntas cuando revise los gráficos:

Hablemos de datos

Como puede ver ahora, leer gráficos no es tan simple y directo como podría parecer. Si bien es importante pensar críticamente y hacerse preguntas inteligentes, puede ser muy útil analizar datos con otras personas. Debata sus interpretaciones y las críticas de los gráficos con sus compañeros y amigos. Descubrirá que pueden ayudarse mutuamente a convertirse en lectores más hábiles de gráficos y datos.

Finalización

Todos pueden ayudar a mejorar la forma en que se toman las decisiones cada vez que leen gráficos con precisión o detectan gráficos engañosos. Con su pensamiento crítico y el conocimiento y las herramientas que acaba de aprender, puede analizar e interpretar mejor los gráficos y beneficiarse de una mayor comprensión de los datos y la información. ¡Ahora es momento de avanzar y conquistar esos gráficos! 

Recursos

• Trailhead: Comparaciones de las variaciones de datos
• Trailhead: Correlación y regresión
• Libro: Edward Tufte (2006): La belleza de la evidencia. Graphics Press
• Libro: Alberto Cairo (2016): El arte veraz: Datos, gráficos y mapas para la comunicación (en inglés). New Riders Publishing
• Libro: Alberto Cairo (2020): Cómo mienten los gráficos: Cómo ser más inteligente en relación con la información visual. W.W. Norton & Company
• Artículo académico: Leo Yu-Hu Lo, et al (2022): Mal informado por la visualización: ¿Qué aprendemos de las visualizaciones que informan de forma incorrecta? Wiley & Sons