Usar histogramas para mostrar distribuciones de variables continuas

Objetivos de aprendizaje

Después de completar esta unidad, podrá:

• Identificar las formas de las distribuciones para variables continuas.
• Describir cómo usar histogramas para representar la distribución de datos.

En la unidad anterior, exploramos las distribuciones de una variable discreta (el color de los dulces). Aprendió que las variables discretas tienen valores separados y distintos, mientras que las variables continuas tienen valores que forman un todo ininterrumpido. En esta unidad, explorará las distribuciones de variables continuas y cómo usar histogramas para representarlas.

El siguiente ejemplo fue adaptado del capítulo sobre distribuciones en Online Statistics Education: Curso de estudio multimedia. Líder del proyecto: David M. Lane, Rice University.

En una serie de 20 pruebas, uno de los autores registró sus tiempos de respuesta al mover el cursor sobre un objetivo. La variable “tiempo de respuesta” es continua y, cuando el tiempo se mide en milisegundos, no hay dos tiempos de respuesta iguales.

El gráfico muestra estos tiempos de respuesta en milisegundos.

Distribuciones de frecuencia agrupada de los tiempos de respuesta

Piense en lo que aprendió sobre las distribuciones de la frecuencia que abordamos en la unidad anterior. Si representó los valores de tiempo de respuesta en la tabla anterior mediante una distribución de la frecuencia, habría 20 valores diferentes, cada uno con un valor de frecuencia 1. Esto no aporta demasiada información. 

Para resolver el problema, puede crear una distribución de frecuencia agrupada donde se representan en una tabla los tiempos de respuesta que se encuentran dentro de varias agrupaciones de igual tamaño (intervalos de valores), tal como se muestra en la tabla.

Para representar en un gráfico las distribuciones de frecuencia agrupada, puede usar un histograma. Las etiquetas en el eje x corresponden a los valores medios de la agrupación que representan. 

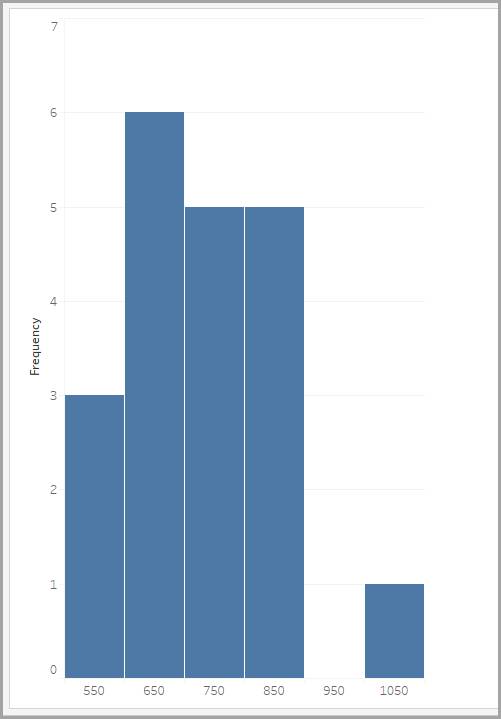
Veremos los histogramas con más detalle un poco más adelante. En primer lugar, exploremos las diferentes formas de distribución y lo que indican sobre los datos de un histograma.

Formas de las distribuciones

Las distribuciones tienen diferentes formas. Pueden ser simétricas, con los valores distribuidos uniformemente alrededor del centro. También pueden tener un sesgo positivo, con más valores hacia la derecha, o un sesgo negativo, con más valores hacia la izquierda.

Imagine que midió la altura de las personas de tres grupos diferentes. Luego, creó un histograma para cada uno a fin de representar la distribución de altura de las personas dentro de ese grupo.

El tamaño de la agrupación es de 2,95 pulgadas, por lo que las alturas de las personas se clasifican en 59 a 61,95 pulgadas, 62 a 64,95 pulgadas, etc. (Tableau Desktop creó automáticamente el tamaño de la agrupación).

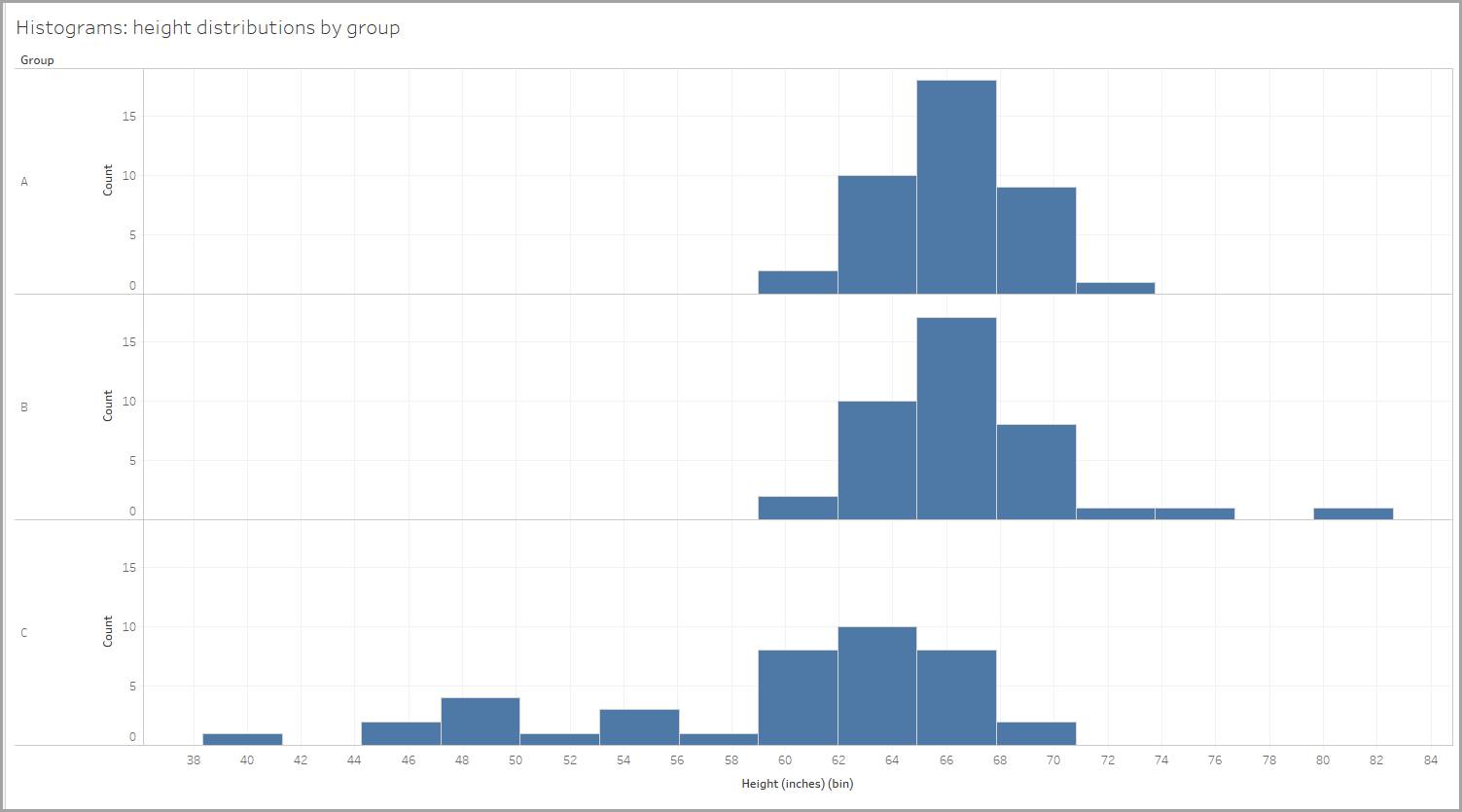
Exploremos la forma de cada distribución. En cada una de las distribuciones que se muestran a continuación, observe que los valores de media (promedio) y mediana (valor medio de los puntos de datos) determinan la forma. 

Distribuciones simétricas

En nuestro ejemplo, la distribución de altura para uno de los grupos es prácticamente simétrica. Si la doblara por la mitad, ambos lados prácticamente coincidirían.

En una distribución completamente simétrica, el centro de los datos es la media (o promedio) y la mediana (el valor medio de los puntos de datos), ya que ambos valores son idénticos. El centro de los datos está representado por ambos valores, y la distribución se extiende de igual manera a ambos lados del centro.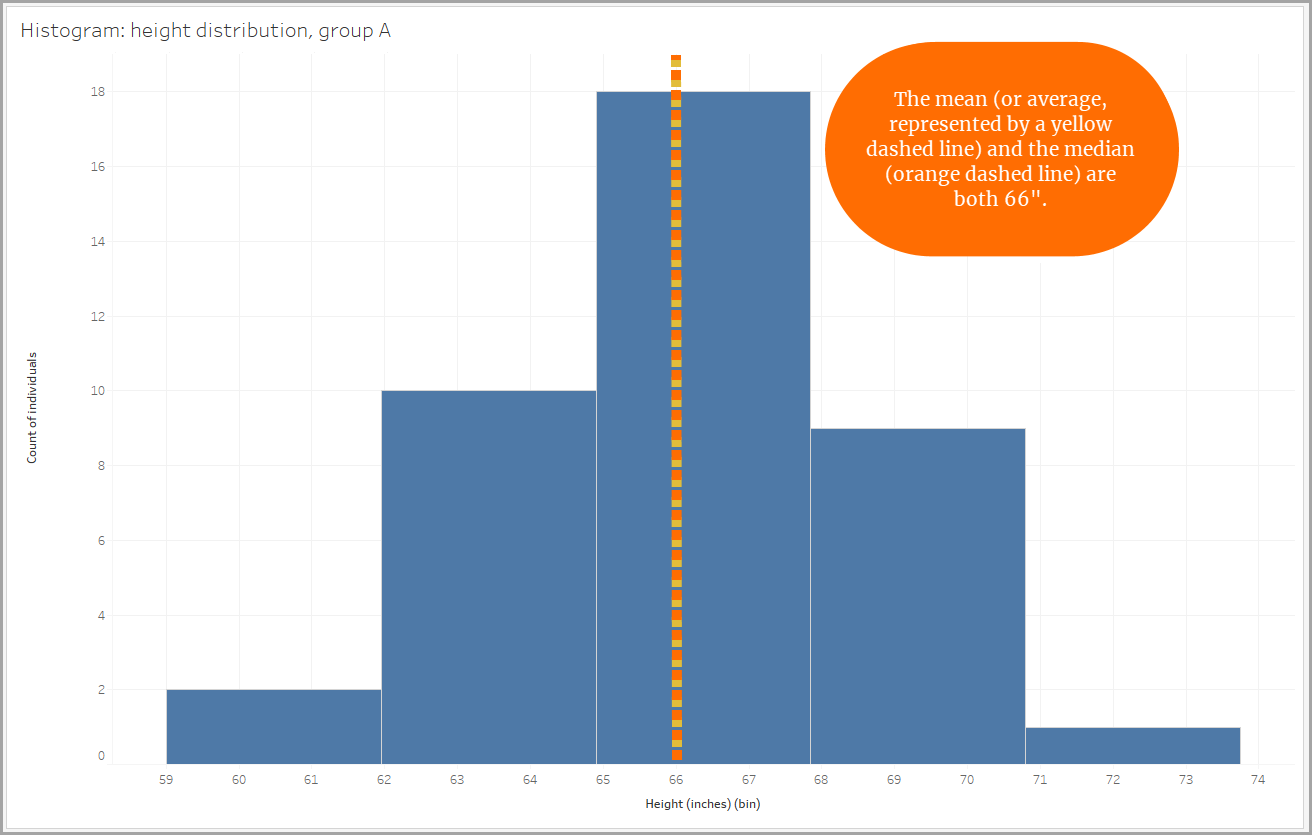

Distribuciones de sesgo positivo

Algunas distribuciones no son simétricas. Si los datos en una distribución se orientan más hacia la dirección positiva que hacia la dirección negativa, se trata de una distribución con un sesgo positivo. El sesgo positivo también se conoce como sesgo a la derecha, porque los datos se extienden hacia la derecha. La “cola” derecha es más larga. Cuando una distribución tiene un sesgo positivo, la mediana es menor que la media (o el promedio).

Por ejemplo, imagine una ciudad cuyos residentes incluyen varios multimillonarios. Los altos ingresos de esos multimillonarios sesgarían los ingresos medios (o promedio) de la ciudad. Los ingresos promedio parecerían más altos de lo que son. Para reflejar verdaderamente la situación económica de todos los residentes de una ciudad, el ingreso promedio sería la mejor opción.

De igual modo, al observar los datos de alturas, un grupo muestra un sesgo positivo debido a la presencia de tres personas que medían cerca de 72" (6 pies) o más. Estas personas más altas hacen que la media sea mayor. Por lo tanto, usar la mediana para conocer la altura del grupo también sería una mejor opción en este caso.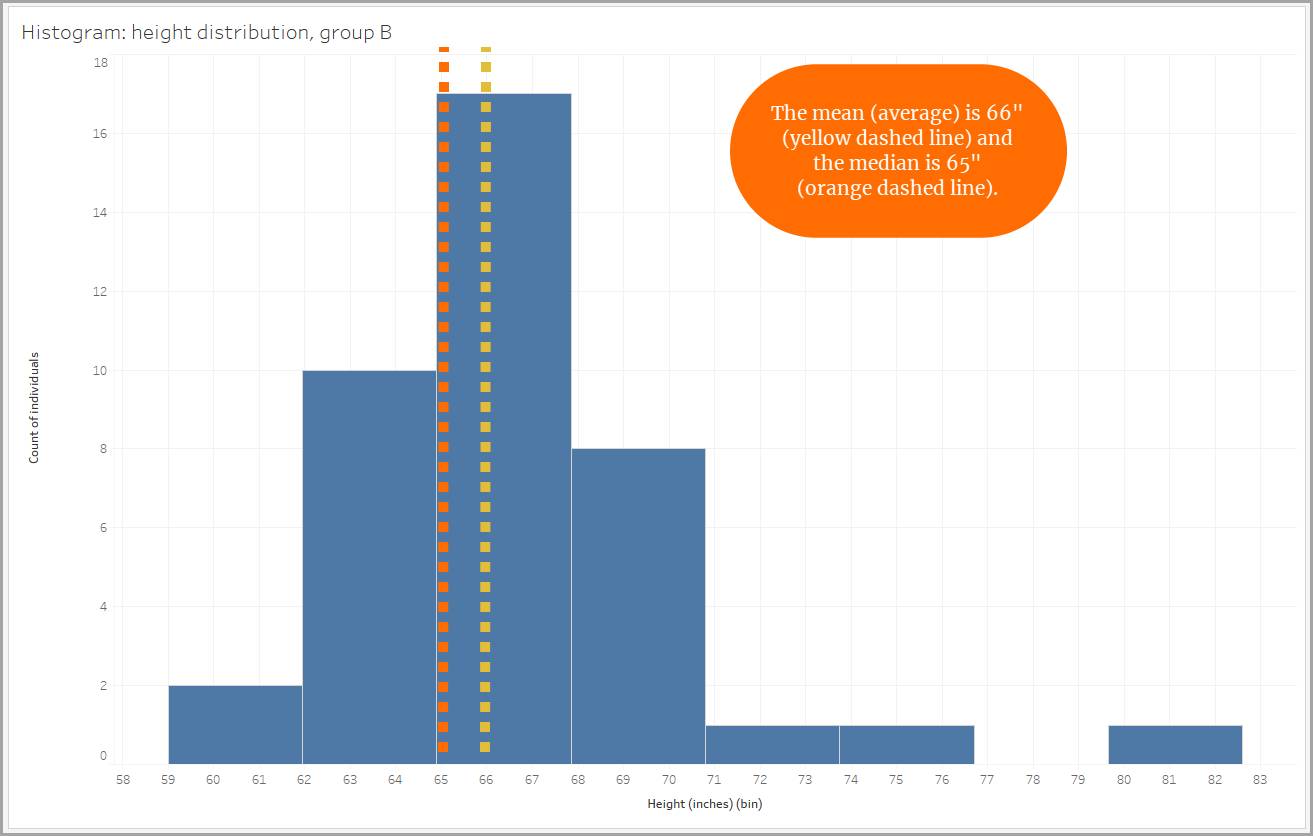

Distribuciones de sesgo negativo

Otra distribución asimétrica es la distribución de sesgo negativo. Los datos en una distribución de sesgo negativo se orientan más hacia la dirección negativa que hacia la dirección positiva. El sesgo negativo también se conoce como sesgo a la izquierda, porque los datos se extienden hacia la izquierda. La “cola” izquierda es más larga. Cuando una distribución tiene un sesgo negativo, la mediana es mayor que la media (o el promedio).

Por ejemplo, imagine una clase de 20 estudiantes. En esta clase, hay dos estudiantes que nunca asistieron a clase ni completaron ninguna tarea. Estos dos estudiantes obtuvieron una calificación final de 0,0. Sus calificaciones de 0,0 afectarían a los resultados de la calificación media (o promedio) de toda la clase, por lo que el rendimiento promedio de los estudiantes parecería más bajo de lo que es. Para reflejar verdaderamente el desempeño de los estudiantes en esta clase, la calificación media obtenida sería una mejor opción.

De igual modo, al observar los datos de alturas, un grupo muestra un sesgo negativo debido a la presencia de personas que medían menos de 60" (5 pies). Estas personas más bajas hacen que la media sea menor.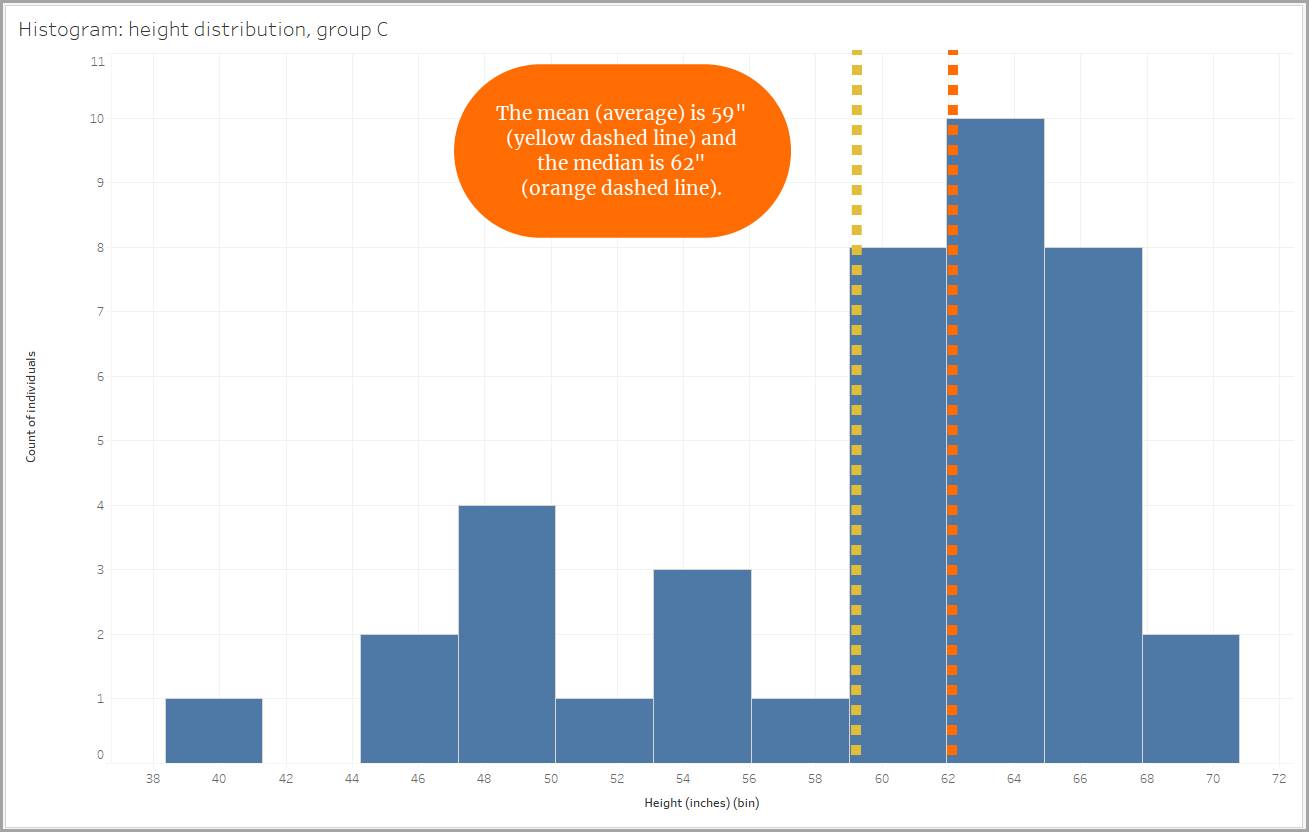

Histogramas

Todos los gráficos que explora en esta unidad son histogramas. Un histograma se parece a un gráfico de barras, pero agrupa los valores de una variable continua en intervalos de igual tamaño, o agrupaciones. 

En este histograma se utiliza un conjunto de datos con información sobre atletas olímpicos. Una de las variables en el conjunto de datos incluye las edades de los atletas. El histograma le permite ver cómo los atletas se dividen en diferentes grupos de edad.

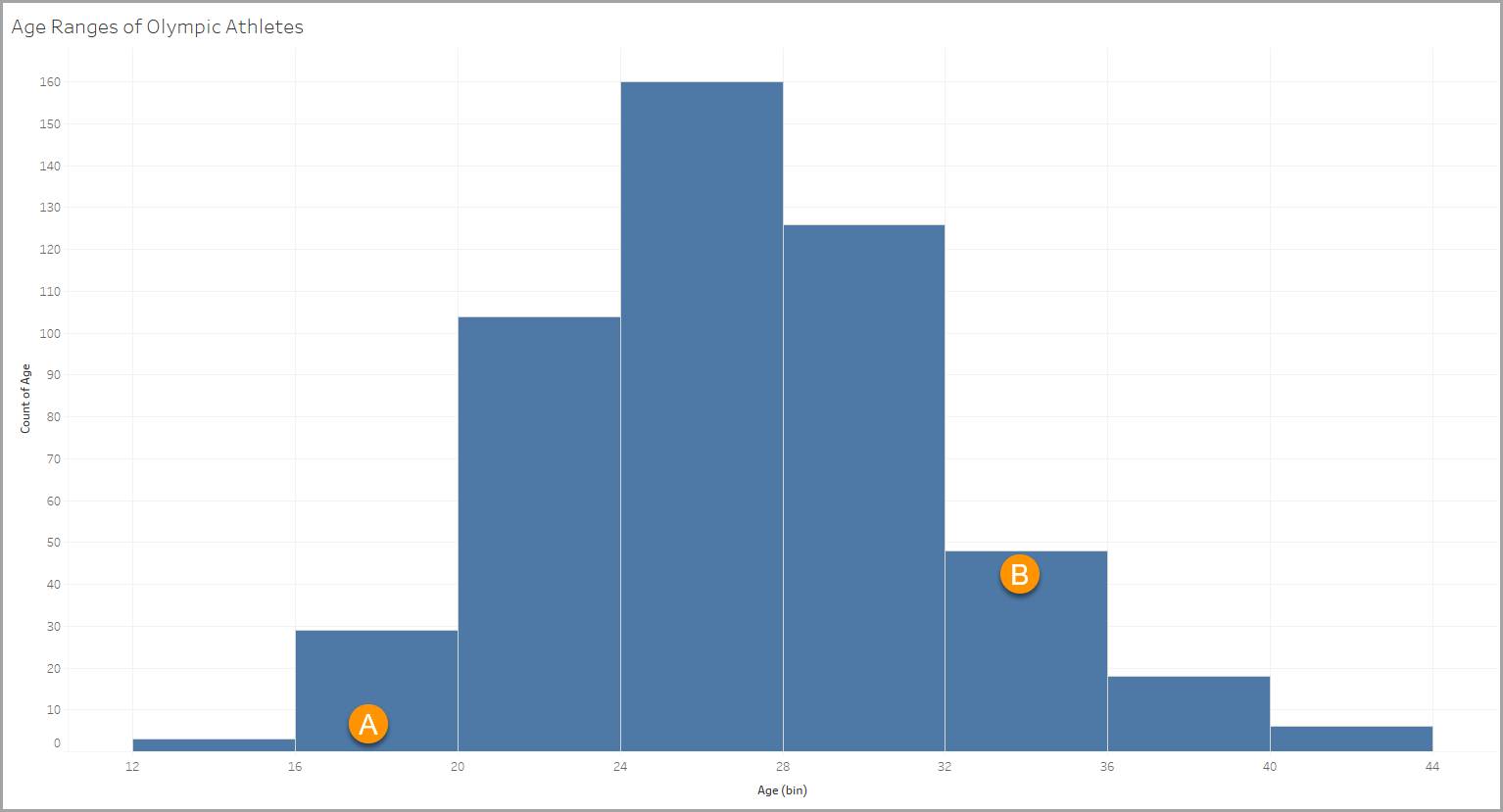
Agrupaciones

Cada agrupación está definida por un intervalo de edad de cuatro años, como 12-15, 16-19 (A), 20-23, 24-27, etc. 

Columnas

Cada columna representa el número de elementos que satisfacen los criterios de la agrupación (en este caso, el intervalo de edad). En nuestro ejemplo, hay 48 atletas en el intervalo de 32 a 35 años (B).

Ya aprendió cómo funcionan las distribuciones de variables continuas organizadas como histogramas. En la siguiente unidad, aprenderá a reconocer distribuciones de variables continuas con diagramas de cajas.

Recursos

• Sitio web: Trabajo de David M. Lane disponible para el público en línea, Introducción a la estadística
• Ayuda de Tableau: Crear un histograma