Usar diagramas de cajas para mostrar distribuciones de variables continuas
Objetivos de aprendizaje
Después de completar esta unidad, podrá:
- Describir cómo se usan los diagramas de cajas para representar la distribución de datos.
- Crear un diagrama de cajas y líneas.
Hasta ahora, exploramos diferentes maneras de visualizar las distribuciones de variables. En esta unidad, descubrirá otro gráfico importante, conocido como diagrama de cajas. Presentados en los años 1970 por el matemático estadounidense John Tukey, los diagramas de cajas representan un método visualmente conciso de ver y contrastar distribuciones de datos.
Las cajas en un diagrama de cajas muestran el 50 % medio de los datos. Estos datos se extienden desde el percentil 25 hasta el percentil 75, con la mediana en el percentil 50.
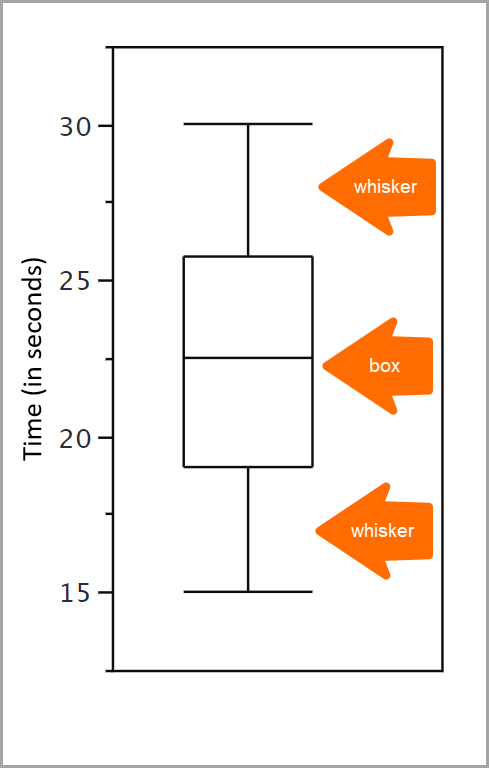
Un percentil expresa una puntuación en comparación con otras puntuaciones dentro de un mismo conjunto de datos. Por ejemplo, imagine que resuelve una prueba para medir su nivel de introversión. En sí misma, su puntuación de introversión puede ser difícil de interpretar para usted. Quizás quiera comparar su puntuación de introversión con la de otros para conocer el porcentaje de personas con puntuaciones de timidez más bajas que la suya. Este porcentaje es un percentil. Si el 65 % de las otras personas que respondieron al cuestionario son menos tímidas que usted, su puntuación es el percentil 65.
Para revisar los resultados, las cajas en un diagrama de cajas muestran el 50 % medio de datos, es decir los percentiles 25 a 75. ¿Pero qué ocurre con los datos que quedan afuera? Ahí entran en juego los bigotes: se trazan fuera de la caja y representan líneas verticales que terminan en un trazo horizontal. Brindan información sobre los valores que no se encuentran dentro del 50 % medio de los datos (la caja), incluidos los valores atípicos. Los valores atípicos pueden entenderse como observaciones atípicas y poco frecuentes, o bien como valores que tienen una desviación extrema respecto del centro de una distribución.
Exploraremos todos estos conceptos en más profundidad más adelante en la unidad.
Crear un diagrama de cajas
El siguiente ejemplo de un diagrama de cajas fue adaptado del capítulo de David M. Lane sobre el tema, que está disponible en Online Statistics Education: A Multimedia Course of Study (Educación sobre estadística en línea: Curso de estudio multimedia). Líder del proyecto: David M. Lane, Rice University.
El autor realizó un experimento en una clase de 31 estudiantes. Cada estudiante recibió una página con 30 rectángulos de colores y su tarea consistía en nombrar los colores lo más rápido posible.
Sus tiempos, en segundos, se registraron como se muestra en la siguiente tabla.
|
14 |
17 |
18 |
19 |
20 |
21 |
|
15 |
17 |
18 |
19 |
20 |
22 |
|
16 |
17 |
18 |
19 |
20 |
23 |
|
16 |
17 |
18 |
20 |
20 |
24 |
|
17 |
18 |
18 |
20 |
21 |
24 |
| 29 |
Usemos este conjunto de datos para crear un diagrama de cajas. Esta es una descripción general de los pasos que necesita para crear uno.
- Calcule los percentiles.
- Trace la caja de acuerdo con los percentiles.
- Determine el tamaño del paso.
- Agregue los bigotes.
- Agregue el valor exterior.
Calcular los percentiles
Recuerde que las cajas en los diagramas de cajas abarcan desde el percentil 25 hasta el percentil 75 de los datos. El percentil 50 se incluye dentro de la caja. La parte inferior de la caja (llamada bisagra inferior) es el percentil 25 y la parte superior de la caja (llamada bisagra superior) es el percentil 75.
En los siguientes pasos, usemos una recta numérica para ver los percentiles.
-
Enumere las puntuaciones de menor a mayor.
-
Determine la mediana, o el valor central. El valor de la mediana se ubica en la mitad, entre el inicio y el final de la secuencia de números. En una secuencia de 31 valores, al posicionarnos en el medio, tendremos 15 valores antes de la mediana y 15 valores después de ella. Por lo tanto, el valor de la mediana es 19.
-
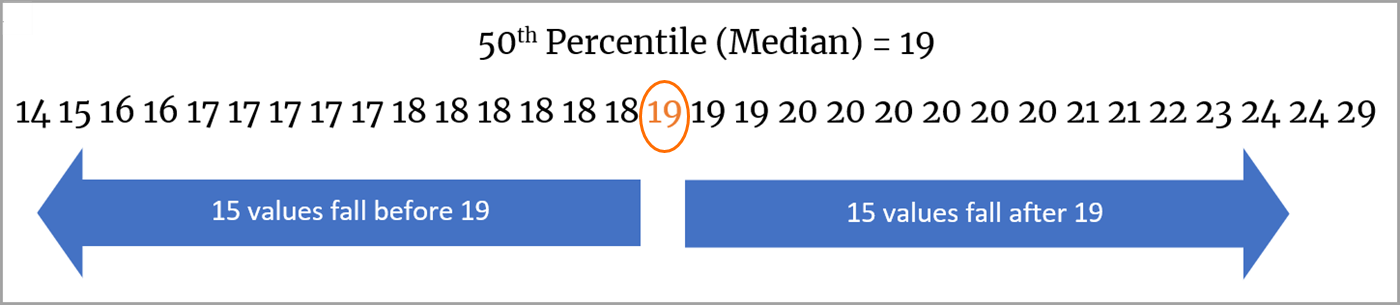
Determine el percentil 25. El valor del percentil 25 se ubica en el medio, entre el inicio de la secuencia y el valor de la mediana. En nuestro ejemplo de 31 valores, la ubicación intermedia tiene 7 valores antes y 7 valores entre ella y la mediana. Por lo tanto, el valor del percentil 25 es 17.
-
Determine el percentil 75. El valor del percentil 75 se ubica en el medio, entre la mediana y el final de la secuencia. En nuestra lista de 31 valores, esta ubicación intermedia tiene 7 valores entre ella y la mediana, y 7 valores entre ella y el final de la secuencia. Por lo tanto, el valor del percentil 75 es 20.
Trazar la caja de acuerdo con los percentiles
Vamos a reunir estos valores y trazar la caja.
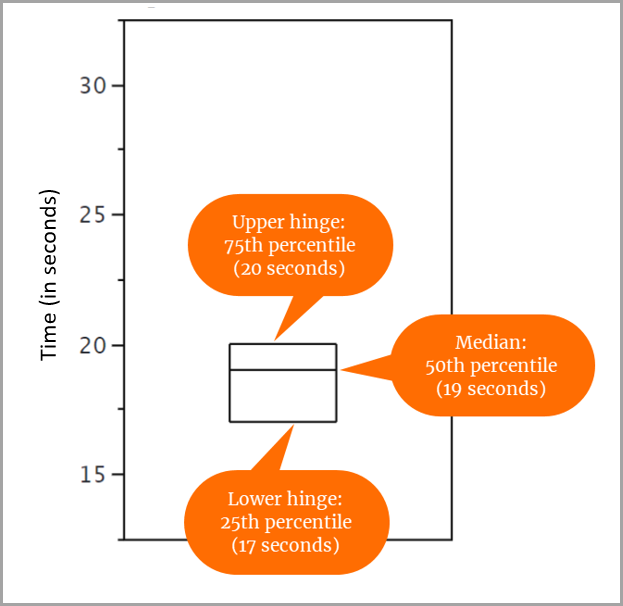
Para nuestro conjunto de 31 puntuaciones, determinamos lo siguiente:
- El valor del percentil 25 es 17.
- El valor del percentil 50 (o mediana) es 19.
- El valor del percentil 75 es 20.
Por lo tanto, la caja se traza del siguiente modo:
- El percentil 25 (bisagra inferior) está alineado con el valor 17 en el eje y.
- El percentil 50 (mediana) está alineado con el valor 19 en el eje y.
- El percentil 75 (bisagra superior) está alineado con el valor 20 en el eje y.
El 50 % medio de los valores de los datos se incluye en la caja.
Nota: Los valores entre el percentil 25 y la mediana también se conocen como segundo cuartil. Los valores entre el percentil 51 (justo después de la mediana) y el percentil 75 se conocen como tercer cuartil. Los valores inferiores al percentil 25 también se conocen como primer cuartil. Los valores superiores al percentil 75 también se conocen como cuarto cuartil. Utilice bigotes y otras marcas para mostrar los valores del primer y el cuarto cuartil
Determinar el tamaño del paso
Ahora puede prepararse para trazar bigotes arriba y debajo de la caja a fin de brindar información adicional sobre la distribución de datos. La ubicación de los bigotes está determinada por los pasos. Un paso se define como 1,5 x ReC. ReC es el rango entre cuartiles.
Aunque esto pueda parecer complejo, el ReC simplemente hace referencia a la diferencia entre el valor de la bisagra superior (percentil 75) y el valor de la bisagra inferior (percentil 25). Recuerde que el 50 % medio de los valores de los datos se encuentran en la caja delimitada por estos valores.
En nuestro conjunto de puntuaciones, el valor de la bisagra superior es 20 y el valor de la bisagra inferior es 17. Por lo tanto, el ReC es 20 menos 17, es decir, 3.
A fin de determinar el tamaño del paso, multiplicamos 3 (el ReC) por 1,5 y obtenemos 4,5 como tamaño del paso.
Agregar los bigotes
Para comprender cómo se trazan los bigotes, primero veamos algunos términos y de qué modo se aplican a las puntuaciones en nuestro ejemplo.
¿Dónde se trazan los bigotes?
Puede trazar los bigotes desde la bisagra superior hasta el valor adyacente superior y desde la bisagra inferior hasta el valor adyacente inferior.
Los bigotes no llegan por completo a los valores exteriores. En cambio, se representa un valor exterior como una o pequeña, y un valor lejano como un asterisco (*).
En nuestro conjunto de datos, los bigotes se extienden desde el valor (20) de la bisagra superior hasta el valor adyacente superior (24) y desde el valor (17) de la bisagra inferior hasta el valor adyacente inferior (14).
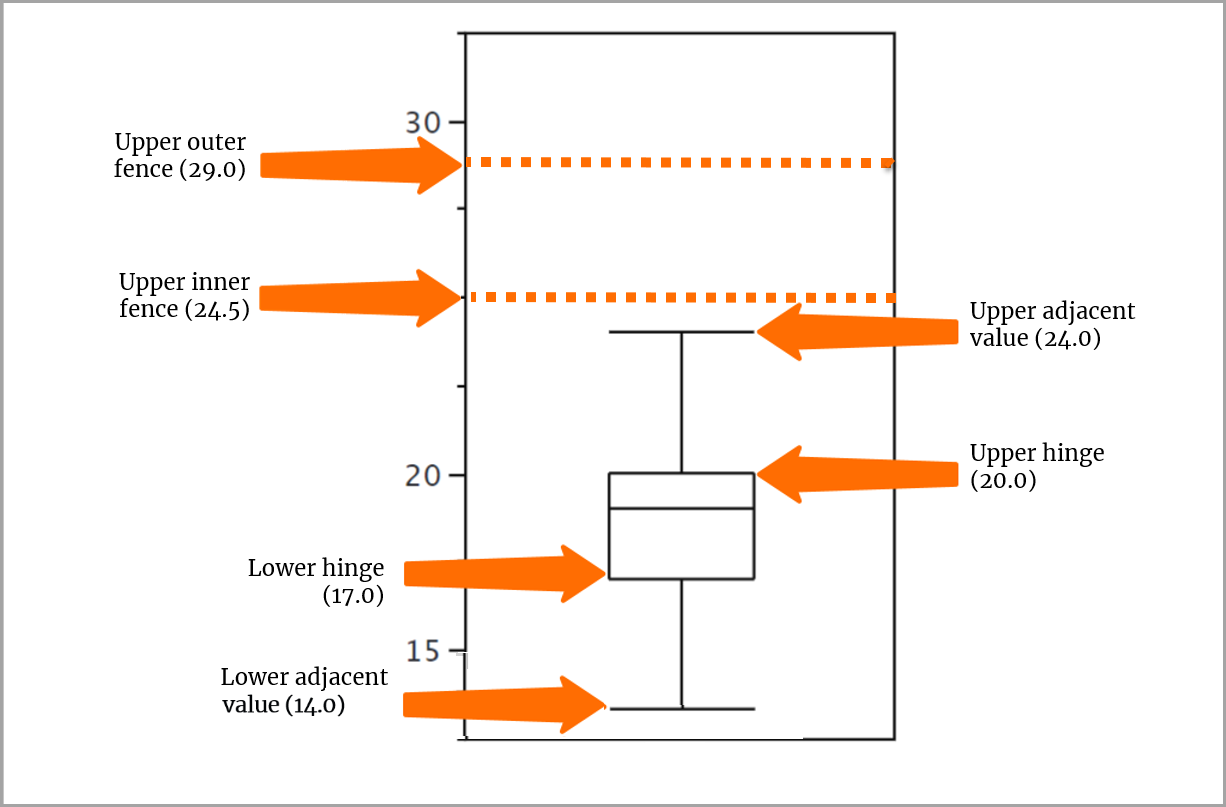
Agregar el valor exterior
Un valor que va más allá del límite interior, pero no más allá del exterior, es un valor exterior. Tenemos uno de estos valores en nuestro conjunto de puntuaciones, 29, que coincide con el valor del límite exterior, pero no va más allá de él. Se utiliza una pequeña o para representar este valor.
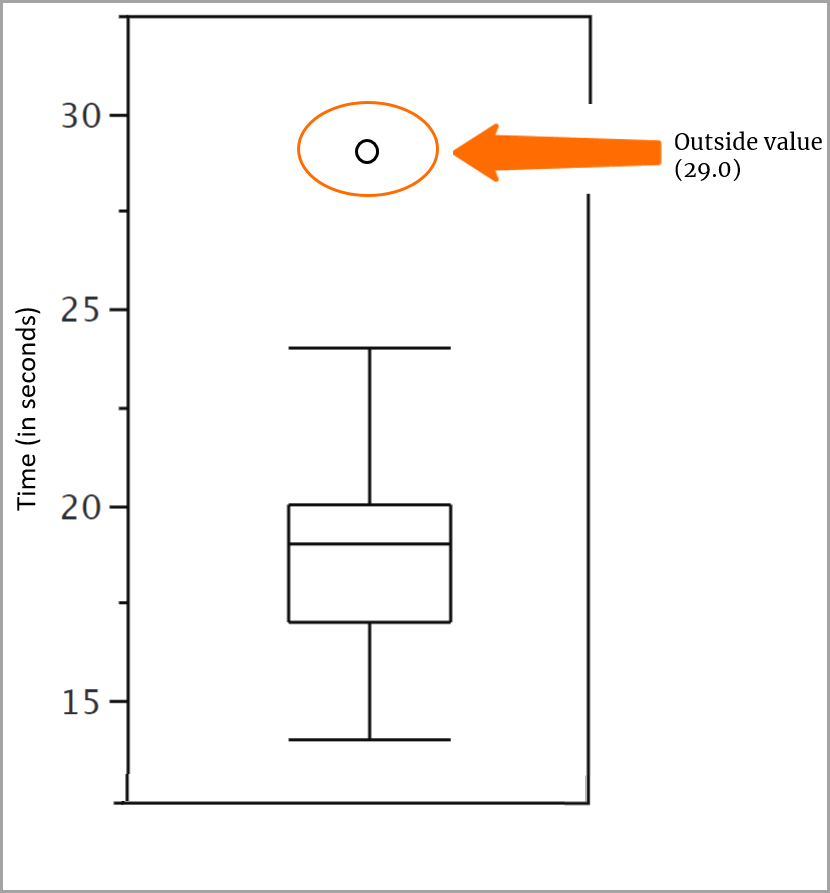
Ahora sí, ¡el diagrama de cajas está listo!
Diagramas de cajas e histogramas
Quizá se está preguntando en qué se diferencian los diagramas de cajas y los histogramas a la hora de mostrar distribuciones.
- Los histogramas usan agrupaciones para trazar la frecuencia de los valores.
- En los diagramas de cajas, el 50 % medio de los datos aparece en la caja, mientras que los valores atípicos (si hay) se trazan por fuera de los bigotes.
Para hacerse una idea de cómo funciona, volvamos a los datos que muestran las formas de las distribuciones de alturas. Compare cómo se ven los datos en un histograma y en un diagrama de cajas.
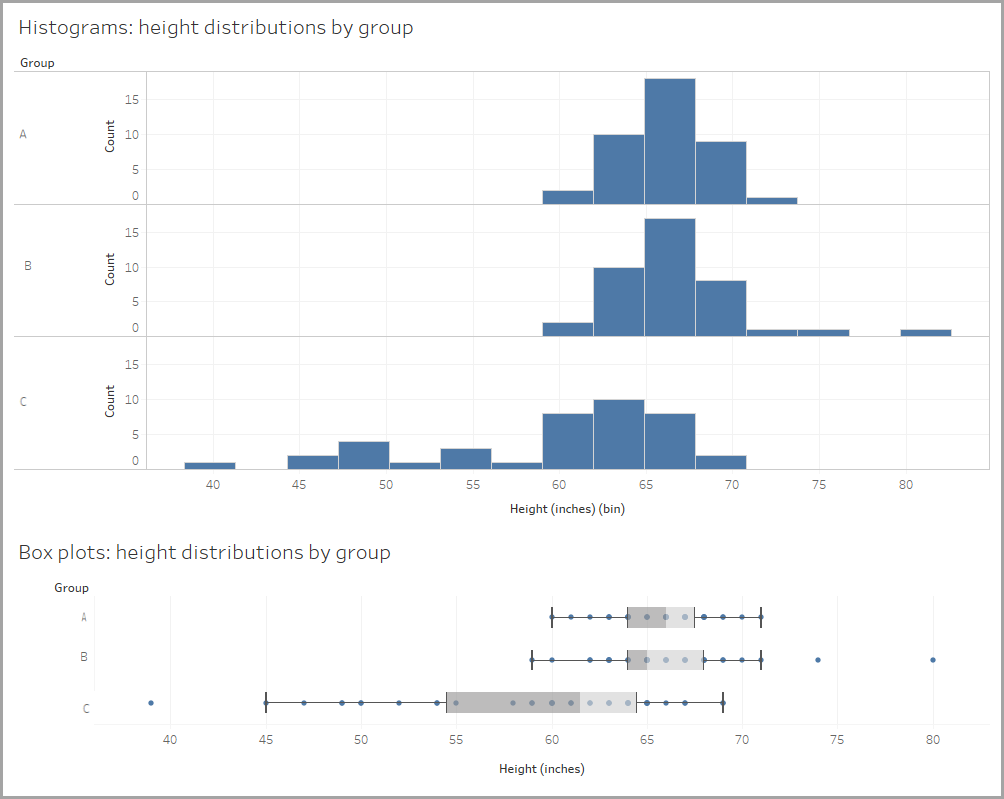
Puede observar que los diagramas de cajas utilizan mucho menos espacio. Esto puede facilitar la comparación de distribuciones. Tres distribuciones situadas una al lado de la otra son más fáciles de comparar con diagramas de cajas que con histogramas. Consulte algunos ejemplos más.
Ahora ya sabe cómo las distribuciones pueden ayudarlo a explorar y comprender los datos y comunicarse con ellos.
