Anzeigen von Verteilungen fortlaufender Variablen mithilfe von Histogrammen
Lernziele
Nachdem Sie diese Lektion abgeschlossen haben, sind Sie in der Lage, die folgenden Aufgaben auszuführen:
- Ermitteln der Formen von Verteilungen fortlaufender Variablen
- Beschreiben, wie die Verteilung von Daten mithilfe von Histogrammen dargestellt wird
In der vorigen Lektion haben Sie sich Verteilungen einer diskreten Variable (die Farbe von Bonbons) angesehen. Wie Sie sich erinnern, haben diskrete Variablen Werte, die getrennt und eindeutig sind, während fortlaufende Variablen Werte haben, die ein ungebrochenes Ganzes bilden. In dieser Lektion erkunden Sie Verteilungen fortlaufender Variablen und ihre Darstellung mithilfe von Histogrammen.
Das folgende Beispiel wurde aus dem Kapitel zu Verteilungen in Online Statistics Education: A Multimedia Course of Study übernommen. Projektleitung: David M. Lane, Rice University, Houston, Texas, USA.
In einer Reihe von 20 Versuchen hat einer der Autoren seine Reaktionszeiten beim Bewegen eines Cursors über ein Ziel aufgezeichnet. Die Variable "Reaktionszeit" ist fortlaufend. Wenn die Zeit in Millisekunden gemessen wurde, waren keine zwei Reaktionszeiten identisch.
Das nachstehende Diagramm zeigt diese Reaktionszeiten in Millisekunden.
Testversion |
Reaktionszeiten in Millisekunden |
Testversion |
Reaktionszeiten in Millisekunden |
|---|---|---|---|
1. |
568 |
11. |
720 |
2. |
577 |
12. |
728 |
3. |
581 |
13. |
729 |
4. |
640 |
14. |
777 |
5. |
641 |
15. |
808 |
6. |
645 |
16. |
824 |
7. |
657 |
17. |
825 |
8. |
673 |
18. |
865 |
9. |
696 |
19. |
875 |
10. |
703 |
20. |
1007 |
Gruppierte Häufigkeitsverteilungen von Reaktionszeiten
Erinnern Sie sich daran, was Sie in der vorherigen Lektion über Häufigkeitsverteilungen gelernt haben. Wenn Sie die Werte für die Reaktionszeit in der vorstehenden Tabelle in einer Häufigkeitsverteilung darstellen, gibt es 20 verschiedene Werte, von denen jeder die Häufigkeit 1 hat. Das ist nicht besonders informativ.
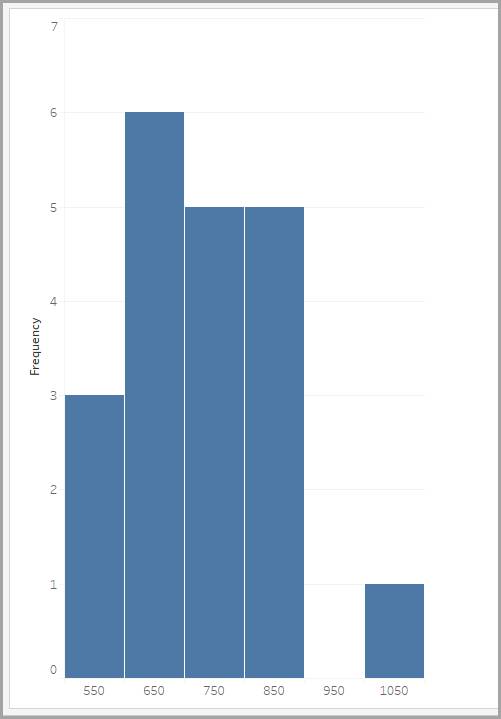
Um dieses Problem zu lösen, können Sie eine gruppierte Häufigkeitsverteilung erstellen, in der Sie die Antwortzeiten tabellarisch auflisten, die in verschiedene gleich große Wertebereiche fallen, wie in der Tabelle dargestellt.
Wertebereich (in Millisekunden) |
Häufigkeit |
|---|---|
500-600 |
3 |
600-700 |
6 |
700-800 |
5 |
800-900 |
5 |
900-1000 |
0 |
1000-1100 |
1 |
Sie können gruppierte Häufigkeitsverteilungen mithilfe eines Histogramms grafisch darstellen. Die Beschriftungen auf der x-Achse sind die mittleren Werte des jeweiligen Wertebereichs.
Wir sehen uns Histogramme später etwas genauer an. Lassen Sie uns zunächst die verschiedenen Verteilungsformen erkunden und was diese über die Daten eines Histogramms aussagen können.
Formen von Verteilungen
Verteilungen gibt es in verschiedenen Formen. Verteilungen können symmetrisch sein, wobei die Werte gleichmäßig um den Mittelpunkt verteilt sind. Sie können aber auch eine positive Schiefe aufweisen, bei der sich mehr Werte auf der rechten Seite befinden, oder eine negative Schiefe, bei der sich mehr Werte auf der linken Seite befinden.
Stellen Sie sich vor, Sie haben die Körpergröße von Personen aus drei verschiedenen Gruppen gemessen und für jede Gruppe ein Histogramm erstellt, um die Körpergrößenverteilung der Personen innerhalb dieser Gruppe darzustellen.
Die Wertebereichsgröße beträgt 2,95 Zoll, sodass die Körpergrößen der Personen in 59–61,95 Zoll, 62–64,95 Zoll usw. eingeteilt werden. (Tableau Desktop hat die Wertebereichsgröße automatisch für uns erstellt.)
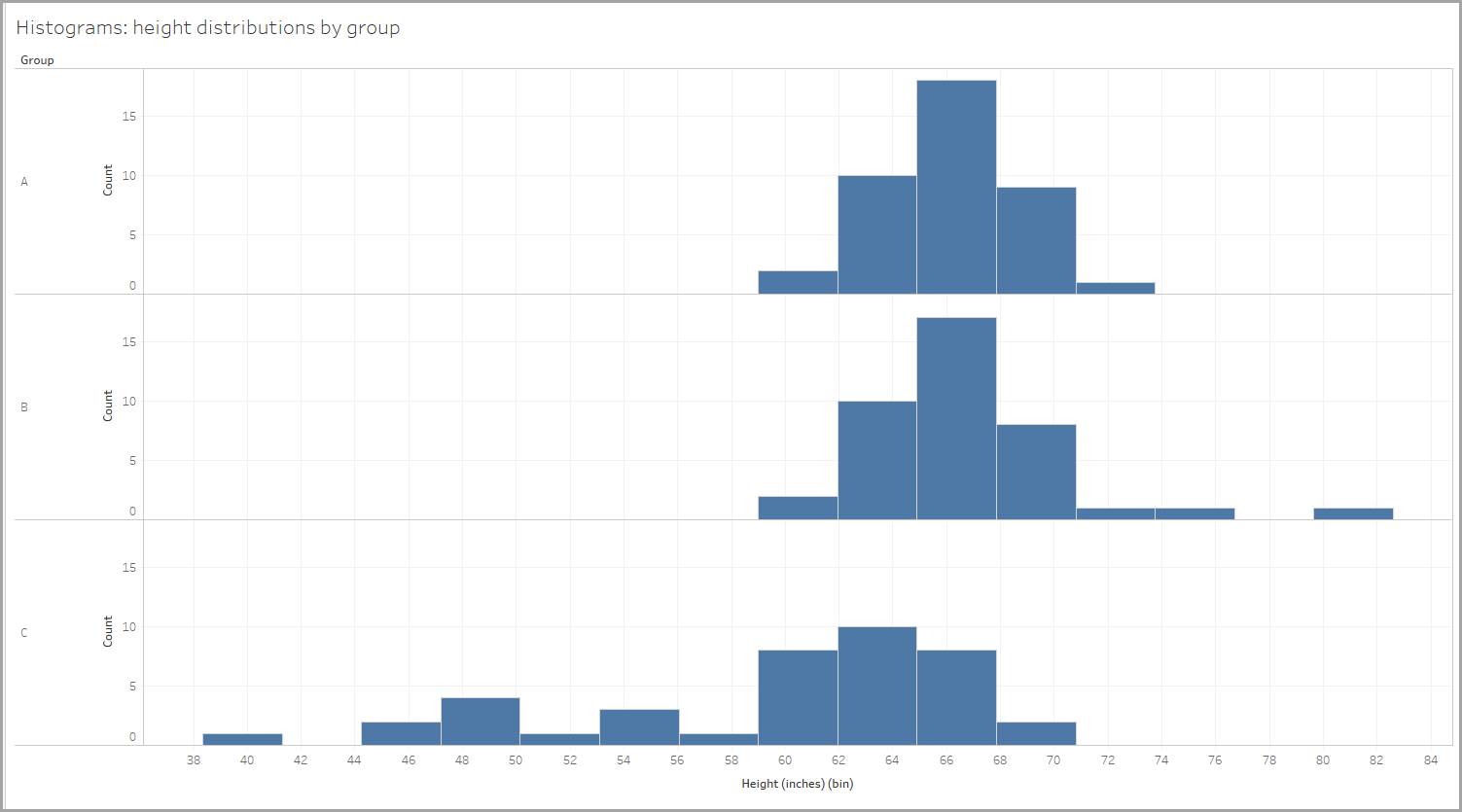
Erkunden wir nun die Form der einzelnen Verteilungen. Beachten Sie bei jeder der nachstehenden Verteilungen, dass die Werte von Mittelwert (Durchschnitt) und Median (dem mittleren Wert der Datenpunkte) die Form bestimmen.
Symmetrische Verteilungen
In unserem Beispiel ist die Körpergrößenverteilung für eine der Gruppen nahezu symmetrisch. Wenn Sie sie in der Mitte falten würden, würden die beiden Seiten fast perfekt übereinstimmen.
Bei einer vollständig symmetrischen Verteilung ist der Mittelpunkt der Daten sowohl der Mittelwert (oder Durchschnitt) als auch der Median (der mittlere Wert der Datenpunkte), da diese Werte gleich sind. Der Mittelpunkt der Daten wird durch beide Werte dargestellt. Die Streuung der Daten erstreckt sich auf beiden Seiten des Mittelpunkts um den gleichen Betrag.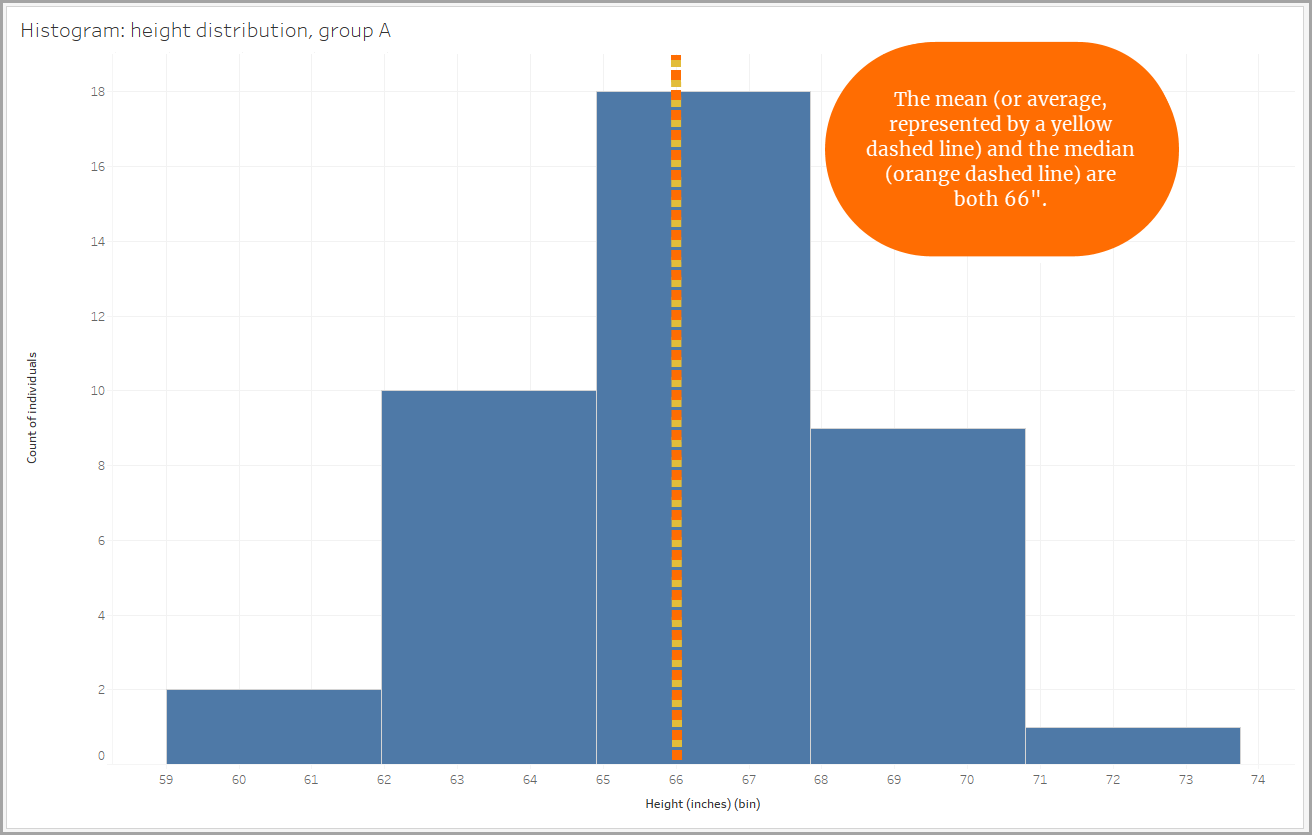
Positiv schiefe Verteilungen
Einige Verteilungen sind nicht symmetrisch. Wenn die Daten in einer Verteilung in positiver Richtung weiter gestreut sind als in negativer Richtung, handelt es sich um eine Verteilung mit positiver Schiefe. Eine positive Schiefe wird auch als Rechtsschiefe bezeichnet, weil sich die Daten nach rechts ausdehnen. Der rechte "Schwanz" ist länger. Wenn eine Verteilung positiv schief ist, ist der Median kleiner als der Mittelwert (bzw. Durchschnitt).
Stellen Sie sich z. B. eine Stadt vor, in der mehrere Milliardäre leben. Die hohen Einkommen dieser Milliardäre würden das mittlere (bzw. durchschnittliche) Einkommen der Stadt verzerren. Das Durchschnittseinkommen würde höher aussehen, als es tatsächlich ist. Um die wirtschaftliche Lage aller Einwohner der Stadt wirklich widerzuspiegeln, wäre das Median der Einkommen die bessere Wahl.
Ähnlich verhält es sich mit unseren Daten zur Körpergröße: Eine Gruppe weist eine positive Schiefe auf, da drei Personen mit einer Körpergröße von fast oder mehr als 72 Zoll (6 Fuß) gemessen wurden. Durch ihre hohe Körpergröße wird der Mittelwert höher. Die Verwendung des Medians, um sich ein Bild von der Körpergröße der Gruppe zu machen, wäre hier die bessere Wahl.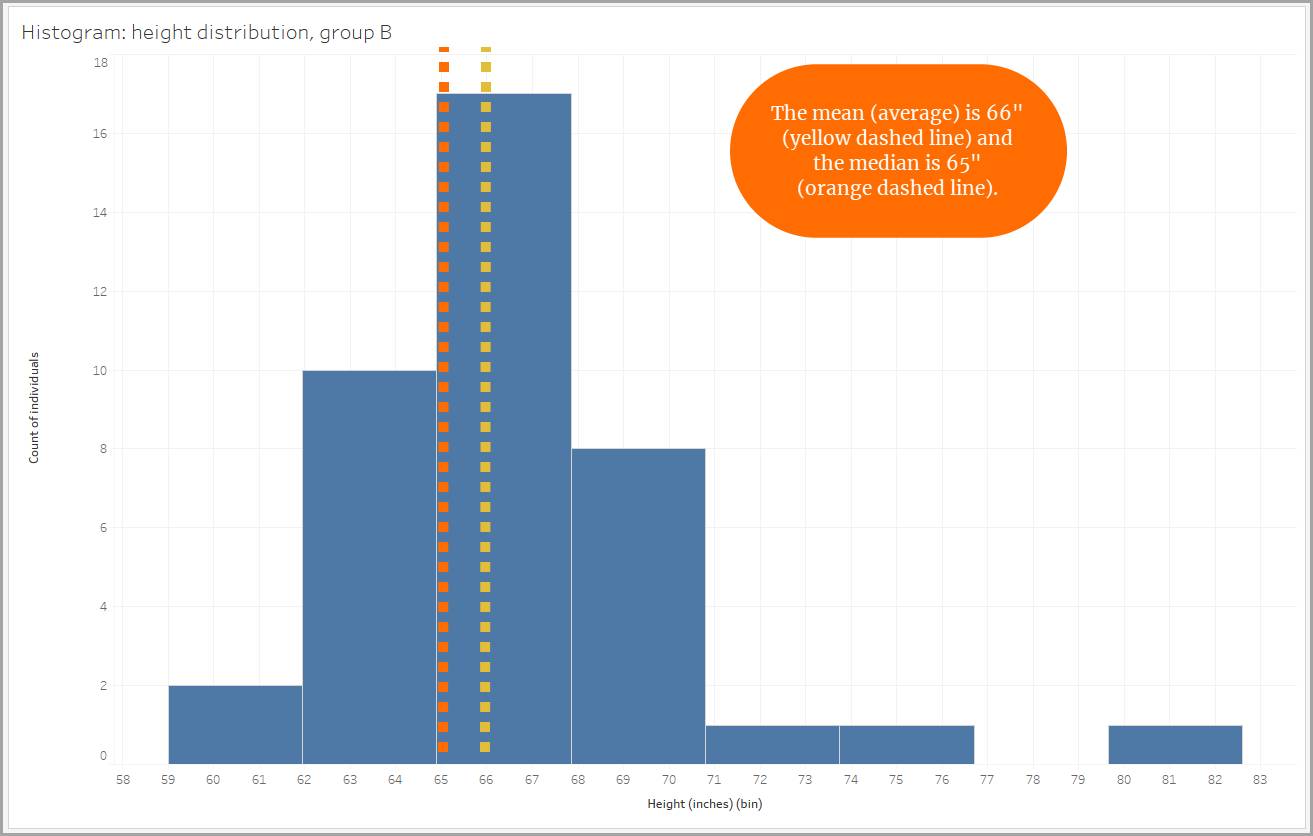
Negativ schiefe Verteilungen
Eine weitere asymmetrische Verteilung ist die negativ schiefe Verteilung. Die Daten in einer negativ schiefen Verteilung sind in negativer Richtung weiter gestreut als in positiver Richtung. Eine negative Schiefe wird auch als Linksschiefe bezeichnet, weil sich die Daten nach links ausdehnen. Der linke "Schwanz" ist länger. Bei einer negativ schiefen Verteilung ist der Median größer als der Mittelwert (bzw. Durchschnitt).
Stellen Sie sich zum Beispiel eine Klasse mit 20 Schülern vor. In dieser Klasse gibt es zwei Schüler, die nie am Unterricht teilgenommen und auch keine Aufgaben erledigt haben. Diese beiden Schüler haben die Endnote 0,0 erhalten. Ihre Noten von 0,0 würden die Ergebnisse des Mittelwerts (bzw. Durchschnittswerts) der Klasse verfälschen und somit die durchschnittliche Leistung der Schüler niedriger erscheinen lassen, als sie tatsächlich ist. Um den Erfolg der Schüler in dieser Klasse korrekt wiederzugeben, wäre der Median der Noten die bessere Wahl.
Ähnlich verhält es sich mit unseren Daten zur Körpergröße: Eine Gruppe weist eine negative Schiefe auf, da Personen mit einer Körpergröße kleiner als 60 Zoll (5 Fuß) gemessen wurden. Durch ihre geringere Körpergröße wird der Mittelwert kleiner.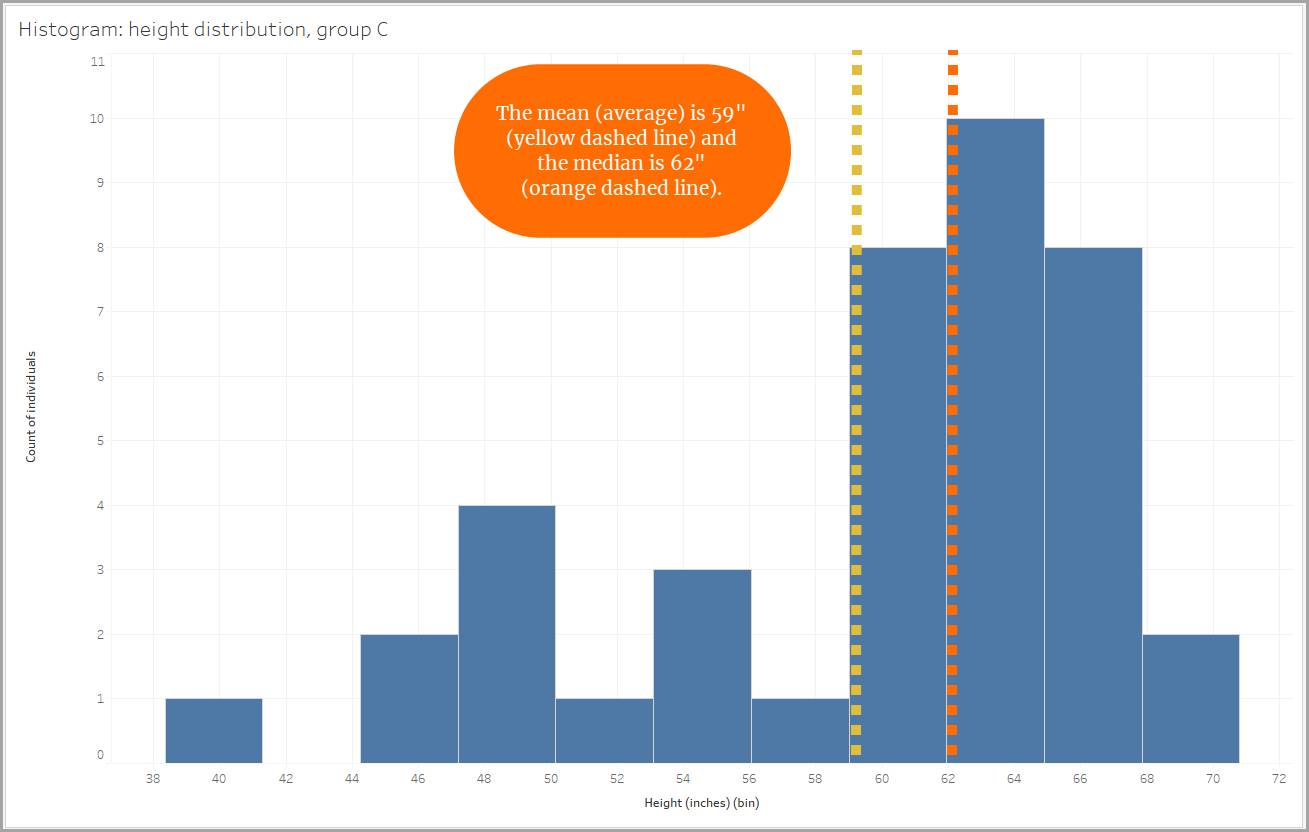
Histogramme
Alle Diagramme, die Sie in dieser Lektion erkunden, sind Histogramme. Ein Histogramm ähnelt einem Balkendiagramm, gruppiert aber die Werte einer fortlaufenden Variablen in gleich große Wertebereiche.
Dieses Histogramm verwendet ein Datenset mit Informationen zu olympischen Athleten. Eine der Variablen im Datenset enthält das Alter der Athleten (von 18 bis 90). Anhand des Histogramms können Sie sehen, wie die Athleten in verschiedene Altersgruppen aufgeteilt sind.
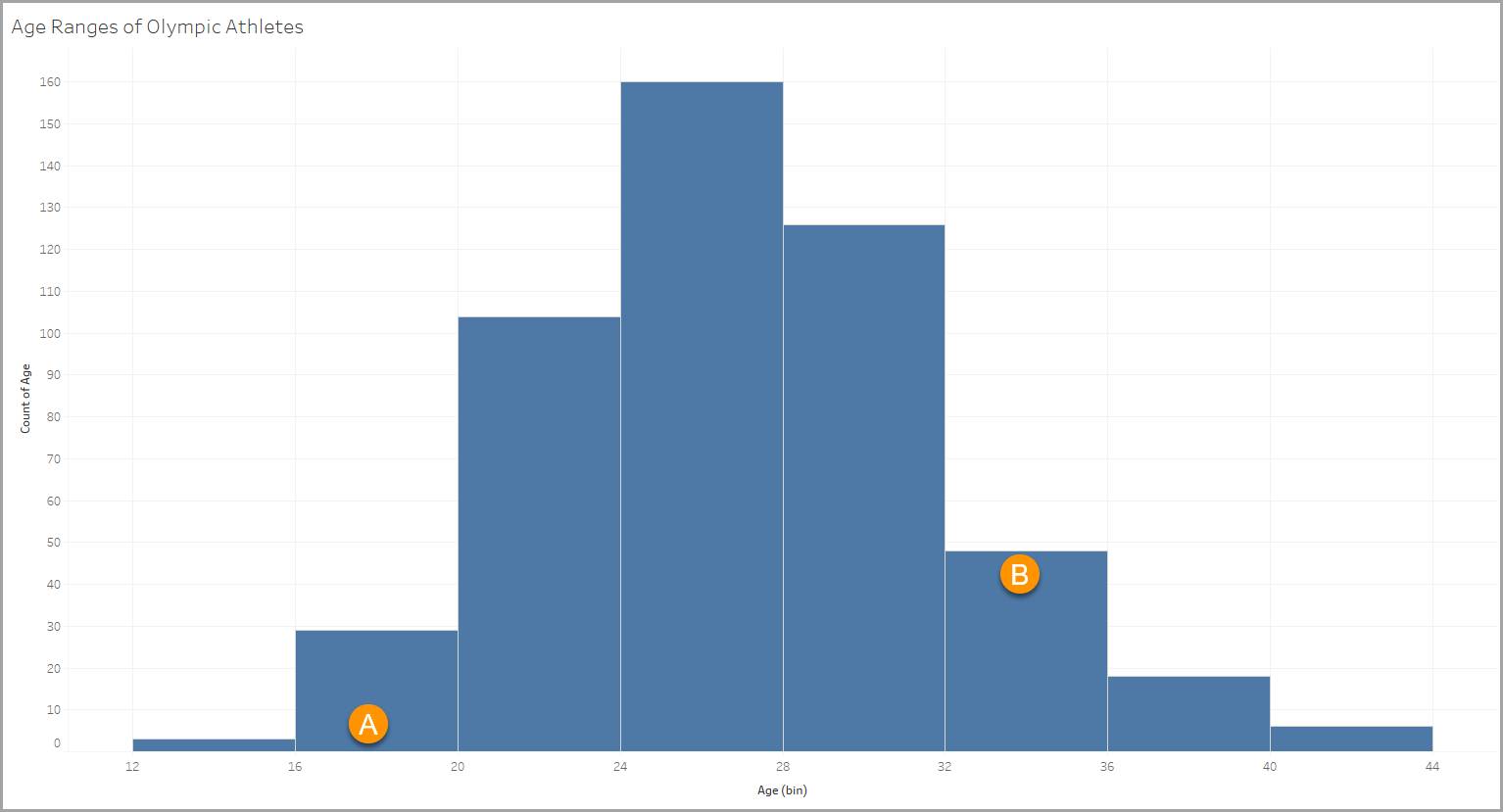
Wertebereiche
Jeder Wertebereich ist durch eine Altersspanne von vier Jahren definiert, z. B. 12–15, 16–19, 20–23, 24–27 usw.
Spalten
Jede Spalte steht für die Anzahl der Elemente, die die Kriterien des Wertebereichs erfüllen (in diesem Fall die Altersspanne). In unserem Beispiel gibt es 48 Athleten in der Altersspanne 32–35 (B).
Sie haben nun einen Blick auf Verteilungen fortlaufender Variablen in Form von Histogrammen geworfen. In der nächsten Lektion lernen Sie, wie Verteilungen fortlaufender Variablen mithilfe von Boxplots dargestellt werden.
Ressourcen
- Website: David M. Lane, Introduction to Statistics, frei zugängliches Online-Buch
- Tableau-Hilfe: Erstellen eines Histogramms