Untersuchen von Korrelation in Daten
Lernziele
Nachdem Sie diese Lektion abgeschlossen haben, sind Sie in der Lage, die folgenden Aufgaben auszuführen:
- Definieren von Korrelation
- Unterscheiden von starken und schwachen Korrelationen
Schritt für Schritt zur Datenkompetenz
Datenkompetenz ist die Grundlage für die einfache Nutzung von und Kommunikation mit Daten.
Im Modul "Datenkompetenz –Grundlagen" werden quantitative Variablen als numerisch messbare Merkmale beschrieben, wie z. B. die Anzahl der Stunden, die täglich vor dem Fernseher verbracht werden, die in km/h gemessene Geschwindigkeit, die jährliche Niederschlagsmenge in einer Stadt, der Umsatz in Euro und die Ausgaben für Marketing.
Wie bestimmen Sie bei der Untersuchung von Beziehungen innerhalb Ihrer Daten, wie eng zwei Variablen, z. B. Umsatz und Höhe der Marketingausgaben, miteinander verbunden sind? Können Sie anhand einer Variable eine andere vorhersagen?
Korrelation und Regression sind wichtige Techniken, um Trends aufzuspüren und Prognosen zu erstellen. Es gibt zwar noch andere wichtige Formen, die in der Analyse verwendet werden, aber wir konzentrieren uns auf die einfachste in der KI und Analyse verwendete Form: lineare Korrelation und Regression.
In dieser Lektion machen Sie sich mit dem Konzept der Korrelation vertraut, die beschreibt, wie eng zwei Variablen miteinander in Beziehung stehen. Sie erfahren, wie hilfreich es ist, mittels Korrelation das Maß der Beziehung zu messen, ohne aber einen kausalen Zusammenhang herzustellen. In der nächsten Lektion erkunden Sie, wie mithilfe linearer Regression der Wert einer Variablen anhand einer anderen Variablen berechnet oder vorhergesagt und wie gemessen werden kann, wie gut das Modell für Ihre Daten geeignet ist.
Was ist Korrelation?
Korrelation ist eine Technik, die zeigen kann, ob und wie eng Paare quantitativer Variablen in Beziehung zueinander stehen.
In dieser Lektion wird die Pearsonsche Korrelation behandelt. Es gibt weitere nichtlineare Korrelationen, auf die hier nicht eingegangen wird.
Besteht beispielsweise ein Zusammenhang zwischen der Anzahl der täglich aufgenommenen Kalorien und dem Körpergewicht? Wiegen Menschen, die mehr Kalorien zu sich nehmen, mehr? Anhand der Korrelation können Sie erkennen, wie stark das Gewicht von Personen mit ihrer Kalorienzufuhr zusammenhängt.
Die Korrelation zwischen Gewicht und Kalorienzufuhr ist ein einfaches Beispiel, aber mitunter weisen die Daten, mit denen Sie arbeiten, nicht die Beziehungen auf, die Sie erwarten. In anderen Fällen vermuten Sie möglicherweise Korrelationen, ohne zu wissen, welche die stärksten sind. Die Korrelationsanalyse hilft Ihnen, Ihre Daten zu verstehen.
Wenn Sie Ihre Korrelationsanalyse beginnen, können Sie ein Streudiagramm erstellen, um die Beziehung zwischen zwei quantitativen Variablen zu untersuchen. Die Variablen werden als kartesische Koordinaten gezeichnet, die angeben, auf welcher horizontalen x-Achse und auf welcher vertikalen y-Achse sich jeder Datenpunkt befindet. Im folgenden Streudiagramm sehen Sie die Beziehung zwischen Umsatz und Ausgaben für Marketing. Es gibt anscheinend eine Korrelation: Wenn eine Variable ansteigt, scheint dies auch für die andere zu gelten.
Die Konzepte in dieser Lektion wurden aus dem kostenlos zugänglichen Online-Buch von David M. Lane, Introduction to Statistics, übernommen.
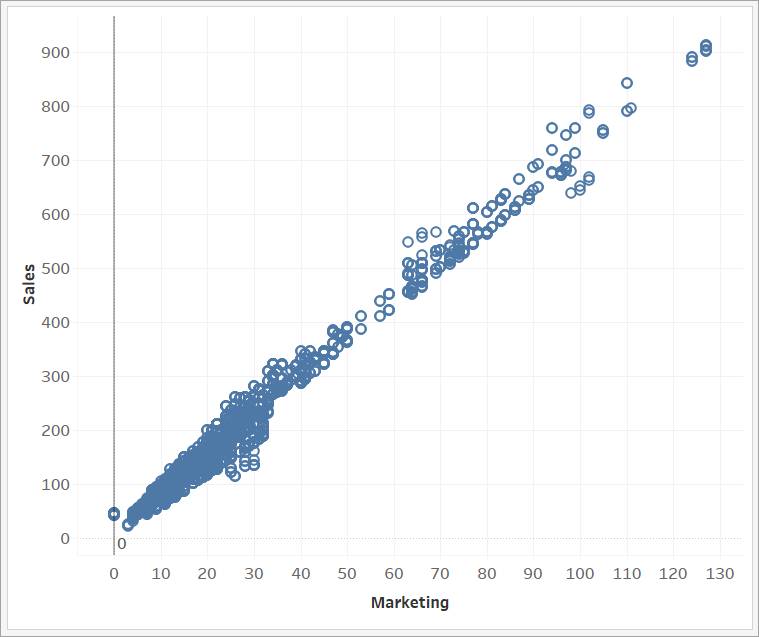
Korrelation kontra Kausalität
Da Sie nun wissen, wie Korrelation definiert und grafisch dargestellt wird, lassen Sie uns erörtern, wie Sie Korrelation besser verstehen können.
Zunächst ist es wichtig zu wissen, dass Korrelation keinesfalls Kausalität belegt.
Die Pearsonsche Korrelation sagt uns nur, wie stark ein Paar quantitativer Variablen linear miteinander in Beziehung steht. Sie erklärt nicht, wie oder warum sie in Beziehung zueinander stehen.
Beispielsweise korreliert der Verkauf von Klimaanlagen mit dem Verkauf von Sonnenschutzmitteln. Aber niemand kauft Klimaanlagen, weil er Sonnencreme gekauft hat, oder umgekehrt. Die Ursache für beide Käufe ist sehr warmes Wetter.
Wie wird Korrelation gemessen?
Die Pearson-Korrelation, auch Korrelationskoeffizient genannt, wird genutzt, um Stärke und Richtung (positiv oder negativ) der linearen Beziehung zwischen zwei quantitativen Variablen zu messen. Bei der Messung von Korrelation in einer Datenstichprobe wird als Symbol der Buchstabe r verwendet. Pearsons r kann von -1 bis 1 reichen.
Wenn r = 1 ist, besteht eine perfekte positive lineare Beziehung zwischen den Variablen, was bedeutet, dass beide Variablen bei steigenden Werten perfekt korrelieren. Wenn r = -1 ist, besteht eine perfekte negative lineare Beziehung zwischen den Variablen. Bei einer perfekten negativen Korrelation nimmt also bei einem Anstieg der einen Variablen die andere Variable in gleichem Maße ab. Wenn r = 0 ist, gibt es keine lineare Beziehung zwischen Variablen.
Bei tatsächlichen Daten können Sie nicht mit den r-Werten -1, 0 oder 1 rechnen.
Im Allgemeinen ist die Korrelation umso stärker, je näher r bei 1 oder -1 liegt, wie die folgende Tabelle zeigt.
| r = | Korrelation |
|---|---|
|
0,90 bis 1 oder -0,90 bis -1 |
Sehr starke Korrelation |
|
0,70 bis 0,89 oder -0,70 bis -0,89 |
Starke Korrelation |
|
0,40 bis 0,69 oder -0,40 bis -0,69 |
Mäßige Korrelation |
|
0,20 bis 0,39 oder -0,20 bis -0,39 |
Schwache Korrelation |
|
0 bis 0,19 oder 0 bis -0,19 |
Sehr schwache oder keine Korrelation |
Einige Quellen zu diesem Thema kategorisieren Korrelationen einfach als stark, mäßig oder schwach.
Bedingungen für lineare Korrelation
Damit Korrelationen aussagekräftig sind, müssen Sie einige Bedingungen beachten: Es müssen quantitative Variablen verwendet werden, es müssen lineare Beziehungen beschrieben werden und die Auswirkungen von Ausreißern müssen berücksichtigt werden. Sie müssen diese Bedingungen vor einer Korrelationsanalyse überprüfen.
1973 entwickelte ein Statistiker namens Francis Anscombe das Anscombe-Quartett, um zu zeigen, wie wichtig es ist, Daten visuell darzustellen, anstatt einfach nur statistische Tests durchzuführen. Die vier Visualisierungen in seinem Quartett zeigen alle dieselbe Trendliniengleichung. Das Quartett veranschaulicht, warum Visualisierungen so wichtig sind , denn sie helfen uns, Trends in unseren Daten zu erkennen, die durch statistische Tests möglicherweise verborgen bleiben.
Im folgenden Beispiel erfüllt nur das Streudiagramm links oben im Quartett das Kriterium der Linearität ohne Ausreißer. Das Streudiagramm rechts oben zeigt keine lineare Beziehung, weshalb ein nichtlineares Modell besser geeignet wäre. Die beiden Streudiagramme unten weisen jeweils Ausreißer auf, die die Ergebnisse erheblich beeinflussen können.
Nachdem Sie sich mit den Konzepten rund um die Statistikmethode der Korrelation vertraut gemacht haben, sind Sie nun bereit für die nächste Lektion, in der Sie lineare Regression kennenlernen.