Verstehen, warum neuronale Netze notwendig sind
Lernziele
Nachdem Sie diese Lektion abgeschlossen haben, sind Sie in der Lage, die folgenden Aufgaben auszuführen:
- Erläutern der Einschränkungen von KI-Modellen, die nur gewichtete Eingaben (Inputs) berücksichtigen
- Beschreiben der Rolle neuronaler Netze für maschinelles Lernen
- Definieren der wichtigsten Komponenten neuronaler Netze
- Beschreiben, wie man die Komplexität neuronaler Netze erhöht, und Definieren von Deep Learning
- Erklären, inwiefern es unmöglich ist, die durch Trainieren ermittelten Gewichtungen und Verzerrungen zu interpretieren
Trailcast
Wenn Sie sich eine Audioaufzeichnung diesem Modul anhören möchten, nutzen Sie den nachstehenden Player. Denken Sie nach dem Anhören dieser Aufzeichnung daran, zur jeweiligen Lektion zurückzukehren, sich die Ressourcen anzusehen und die zugehörigen Aufgaben zu absolvieren.
Die Notwendigkeit neuronaler Netze
Eine Unterhaltung über KI ist erst vollständig, wenn neuronale Netze angesprochen werden. Da neuronale Netze wichtige Instrumente für das Training von KI-Modellen sind, ist es gut, eine Vorstellung davon zu haben, was neuronale Netze sind. Doch bevor wir uns mit den Details befassen, sollten wir zunächst darauf eingehen, warum wir neuronale Netze überhaupt brauchen.
In der vorigen Einheit haben Sie gelernt, dass wir ein KI-Modell trainieren können, indem wir es die Bedeutung der einzelnen Eingaben schätzen und überprüfen lassen. Das Beispiel mit dem Milcheinkauf war aber eigentlich zu stark vereinfacht. Unser Modell würde uns in dieser Form nur ziemlich grobe Schätzungen liefern. Um zu verstehen, warum das so ist, sehen wir uns zwei Szenarien an.
- Es regnet an einem Dienstagabend. Sie möchten lieber nicht nass werden und beschließen (wie viele andere auch), dass der Einkauf bis morgen warten kann. In diesem Szenario ist der Regen ein wichtiger Faktor.
- Es regnet am Samstagnachmittag. Für viele Menschen ist dies die einzige Zeit in der Woche, in der sie einkaufen gehen können. Der Laden wird also voll sein, egal ob es regnet oder nicht. In diesem Szenario macht der Regen also keinen großen Unterschied.
Das Problem ist, dass unser ursprüngliches Modell dem Regen nur eine Gewichtung zuweisen kann, wir aber wissen, dass die Sache etwas komplizierter ist. Es gibt jedoch eine Lösung und die beginnt damit, die beiden Szenarien in zwei separaten Diagrammen darzustellen. Auch hier steht die Linienstärke wieder für die Bedeutung. Im ersten Diagramm haben "Wochenende" (W) und "Zeit" (T) geringes Gewicht, während "Regen" (R) große Bedeutung hat. Im zweiten Diagramm ist "Wochenende" wichtig, während "Zeit" und "Regen" unwichtig sind.
Wir wissen, dass diese beiden Szenarien wichtig sind, da wir clever und erfahrene Milcheinkäufer sind. Aber ein Computer, der gerade erst anfängt, etwas über den Einkauf von Milch zu lernen, weiß zunächst gar nichts! Er muss viele Szenarien in Betracht ziehen: Wochenende-Abend-Regen, Wochentag-Morgen-Sonne und so weiter. Anstelle von zwei Diagrammen würden acht Diagramme die verschiedenen Szenarien, die Ihnen begegnen könnten, wahrscheinlich besser abbilden.
Das sind eine ganze Menge ähnlicher Diagramme. Da die drei Inputs immer "Wochenende", "Zeit" und "Regen" sind, können Sie sie übereinander legen. Wenn Sie die Outputs so verschieben, dass sie sich nicht berühren, entsteht ein kombiniertes Diagramm, das so aussieht:
Die Bedeutung der einzelnen Szenarien hängt von den spezifischen Eingaben ab. Die Bedeutung zu kennen, ist jedoch nur die halbe Miete. Jedes Szenario muss sich auf seine eigene Weise auf die endgültige Schätzung auswirken.
Der Milcheinkauf beim Szenario Wochenende-Nachmittag-Sonne sollte beispielsweise viel länger dauern. Wir legen für dieses Szenario daher einen Anpassungswert von +5 fest. Wenn wir nun eine Schätzung berechnen, ergibt sich ein höherer Wert. Wenn wir schon dabei sind, versehen wir das Szenario Wochentag-Morgen-Regen mit einer Anpassung von -4, da wir wissen, dass der Milcheinkauf zu dieser Zeit am schnellsten geht.
Jedes Szenario erhält seine eigene Anpassung, die wir als Verzerrung bezeichnen. In diesem Fall ist eine Verzerrung eine gute Sache, denn sie hilft uns, eine genauere Schätzung zu erhalten. Zeichnen wir nun unser Diagramm neu, um die Verzerrung der einzelnen Szenarien zu berücksichtigen.
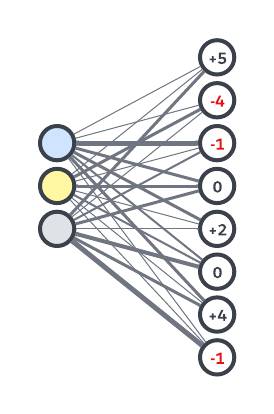
Und was machen wir nun mit diesen acht Szenarien und ihren Verzerrungen? Wir setzen auch hier wieder clevere Mathematik ein, um sie zu einer endgültigen Schätzung zu kombinieren. Einige Szenarien sollten mehr beitragen als andere, also brauchen wir mehr Gewichtungen! Wir können unser Diagramm aktualisieren, um zu zeigen, wie die Szenarien mit unterschiedlicher Gewichtung zur endgültigen Schätzung beitragen.
Das ist unser neues Modell. Mehr Verbindungen bedeuten hoffentlich bessere Schätzungen. Dieses Netz von Verbindungen, die durch Gewichtungen und Verzerrungen bestimmt werden, ist ein Beispiel für ein neuronales Netz. Der Begriff wurde gewählt, weil die Verbindungen, die durch Erfahrung (Daten) geprägt werden, der Verknüpfung von Neuronen im Gehirn ähneln.
Und obwohl Szenario ein gutes Einsteigerwort für die Beschreibung einer einzigartigen Kombination von Faktoren ist, sollten wir dafür eigentlich den Fachbegriff Knoten verwenden. So nennen das KI-Experten, und wir werden diesen Begriff in Zukunft auch verwenden.
Erhöhen der Komplexität neuronaler Netze
Unser neues Milcheinkaufsmodell ist ein recht einfaches Beispiel für ein neuronales Netz. In der Praxis können diese Netze recht komplex werden. Sehen wir uns einige der Möglichkeiten an, wie Wissenschaftler neuronale Netze entwerfen, um bessere Ergebnisse für bestimmte Aufgaben zu erzielen.
Zunächst werden Sie sich vielleicht fragen, warum wir acht Knoten zwischen unseren Inputs und dem Output gewählt haben. Diese Zahl bietet tatsächlich eine gewisse Flexibilität. Wir wissen, dass wir mit gar keinen Knoten nur grobe Schätzungen erhalten. Genauso kann es sein, dass zu wenige Knoten nicht alle Nuancen des Systems erfassen, das wir zu modellieren versuchen. Aber auch zu viele Knoten sind ein Problem. Wir wollen nicht, dass der Computer mehr Berechnungen durchführt als nötig. Es gibt also einen "Sweet Spot" für die Anzahl der Knoten, bei dem wir mit dem geringsten Aufwand gute Ergebnisse erzielen. Die Wahl der richtigen Knotenzahl ist Teil der Entwicklung eines guten neuronalen Netzes.
Wir können noch etwas tun, um zu erreichen, dass künstliche neuronale Netze unseren eigenen, organischen Netzen ähnlicher werden. Es hat damit zu tun, dass unser Verstand oft von einer Idee zur nächsten springt, um Verbindungen zwischen zwei Dingen zu finden, die nicht offensichtlich miteinander in Beziehung stehen. Einige der brillantesten Erkenntnisse sind das Ergebnis mehrerer solcher Sprünge. Wie wäre es also, wenn wir ein neuronales Netz erstellen könnten, das auch mehr Sprünge machen kann? Das wäre toll, und es ist auch möglich! Wir fügen dazu weitere Knoten als Ebenen hinzu und verbinden jeden Knoten mit seinem Nachbarn.
Das Trainieren von KI durch Hinzufügen zusätzlicher Ebenen, um verborgene Beziehungen in Daten zu finden, wird als Deep Learning bezeichnet. Aufgrund der verfügbaren hohen Rechenleistung sind viele neuronalen Netze so konzipiert, dass sie aus mehreren Ebenen bestehen. Auch hier liegt die optimale Anzahl der Ebenen an einem Punkt, an dem sich die Zahl der erforderlichen Berechnungen und die Qualität der Ergebnisse, die sie liefern, die Waage halten.
Schluss mit Kopfrechnen, das ist Mathematik für neuronale Netze
Nun kommen wir zu diesen Berechnungen. Bis jetzt haben wir den mathematischen Teil des Trainings neuronaler Netze immer elegant ausgelassen. Dafür gibt es mehrere Gründe. Punkt 1: Die mathematischen Formeln können sehr schnell sehr kompliziert werden. Hier ist zum Beispiel ein Ausschnitt aus einer wissenschaftlichen Arbeit über neuronale Netze:
Ja, da geht es schon zur Sache!
Punkt 2: Die genaue Mathematik hängt von der Art der Aufgabe ab, für die Sie das neuronale Netz trainieren. Punkt 3: Die Mathematik wird mit jeder neuen wissenschaftlichen Arbeit aktualisiert, da wir ständig mehr darüber lernen, was beim Training verschiedener Modelle besser funktioniert.
Beim Entwerfen eines neuronalen Netzes muss man also die Zahl der Knoten, die Zahl der Ebenen und die geeignete Mathematik für die Aufgabe auswählen, für die es trainiert wird. Wenn die Modellarchitektur fertig ist, lassen Sie den Computer all diese ausgeklügelten mathematischen Formeln einsetzen, um seine Guess-and-Check-Routine auszuführen. Am Ende wird er die besten Gewichtungen und Verzerrungen ermitteln, um gute Schätzungen zu liefern.
Und damit kommen wir zu dem Teil, der an künstlichen neuronalen Netzen ein wenig beunruhigend ist. Stellen Sie sich einen erfahrenen Talentsucher vor, der nach dem nächsten großen Fußballspieler sucht. Nach seiner Vorgehensweise gefragt, könnte er beispielsweise sagen: "Ich weiß es, wenn ich ihn sehe.". Er kann nicht erklären, wie er ein Talent erkennt, er erkennt es einfach. Genauso kann unser neuronales Netz nicht erklären, warum bestimmte Faktoren wichtig sind. Wir können uns natürlich die Werte ansehen, die den einzelnen Gewichtungen und Verzerrungen zugeordnet sind, doch die Relevanz einer Zahl, die das Ergebnis einer Verbindung zu einer Verbindung zu einer Verbindung ist, wird uns verborgen bleiben.
So wie der Verstand des Talentsuchers für uns unergründlich ist, so ist es auch unser neuronales Netz. Da wir die Ebenen zwischen Input und Output nicht beobachten, nennt man sie versteckte Ebenen.
Zusammenfassung
Zusammenfassend lässt sich sagen, dass neuronale Netze eine Mischung aus Knoten, Ebenen, Gewichtungen, Verzerrungen und jeder Menge Mathematik sind. Zusammen ahmen diese Komponenten unsere eigenen organischen neuronalen Netze nach. Jedes neuronale Netz ist sorgfältig auf eine bestimmte Aufgabe abgestimmt. Vielleicht ist es gut darin, Regen vorherzusagen, vielleicht kategorisiert es Pflanzen oder vielleicht hält es Ihr Auto auf der Autobahn in der Mitte der Fahrspur. Ganz gleich was ihre Aufgabe ist, neuronale Netze sind ein wichtiger Bestandteil dessen, was KI magisch erscheinen lässt. Und jetzt wissen Sie auch ein wenig darüber, wie diese Magie funktioniert.
Ressourcen