Understand the Need for Neural Networks
Learning Objectives
After completing this unit, you’ll be able to:
- Explain the limitation of AI models that only consider the weight inputs.
- Describe the role of neural networks in machine learning.
- Define the major components of neural networks.
- Describe how complexity is added to neural networks, and define deep learning.
- Explain how it’s impossible to interpret the weights and biases determined through training.
Trailcast
If you'd like to listen to an audio recording of this module, please use the player below. When you’re finished listening to this recording, remember to come back to each unit, check out the resources, and complete the associated assessments.
The Need for Neural Networks
No conversation about AI is complete without mentioning neural networks. Neural networks are important tools for training AI models, so it’s good to have some idea of what they are. But before we get into the details, let’s first discuss why we need neural networks in the first place.
In the previous unit, you learned that we can train an AI model by letting it guess-and-check the importance-weight of each input. But the milk run example was actually overly simplified. Our model would give us pretty rough estimates. To understand why, let’s consider two scenarios.
- It’s raining on a Tuesday evening. You’d rather not get wet, so you (and many others like you) decide shopping can wait until tomorrow. In this scenario, rain is a significant factor.
- It’s raining on Saturday afternoon. For many people, this is the only time of week when they can go shopping. So the store will be busy, rain or shine. In this scenario, rain doesn’t make much difference.
The problem is that our original model can only assign one weight to rain, but we know it’s more complicated than that. There is a solution, though, and it starts by representing the two scenarios in two separate graphs. Again, line thickness shows importance. In the first, “weekend” and “time” are weak, while “rain” is strong. For the second, “weekend” is strong, while “time” and “rain” is weak.
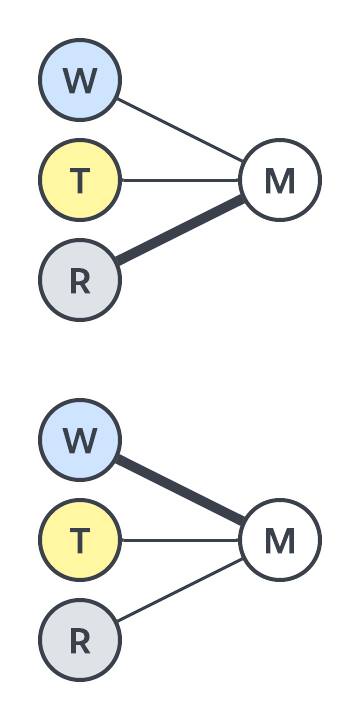
We know these two scenarios are significant because we’re smart and have experience buying milk. But a computer just starting to learn about milk runs doesn’t know anything yet! It has to consider many scenarios: weekend-evening-rain, weekday-morning-shine, and so forth. Instead of two graphs, eight might better represent the kinds of scenarios you encounter.
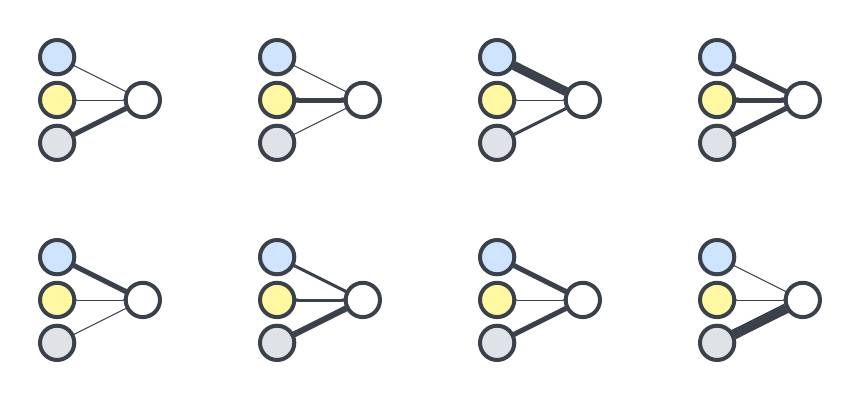
That’s a lot of very similar graphs. Since the three inputs always represent “weekend,” “time,” and “rain,” you can overlap them. If you move the outputs so they aren’t touching, you get a combined graph that looks like this.
The importance of each scenario depends on the specific inputs. But knowing the importance is only half the battle. Each scenario needs to affect the final estimate in its own way.
For example, the weekend-afternoon-shine milk run should take much longer. So let’s give it an adjustment of +5. When we do the math to calculate an estimate, it results in a larger number. While we’re at it, let’s give the weekday-morning-rain scenario an adjustment of -4 since we know milk runs are shortest at that time.
Each scenario gets its own adjustment, which is what we call a bias. In this case, bias is a good thing because it helps us get a more accurate estimate. Let’s redraw our graph to include the bias of each scenario.
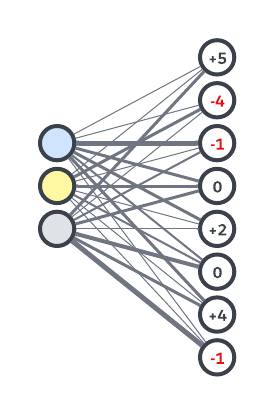
So what do we do with these eight scenarios and their biases? Using some more clever math, we can combine them into a final estimate. Some scenarios should contribute more than others, so you guessed it, we need more weights! We can update our graph to show how the scenarios connect to the final estimate with different strengths.
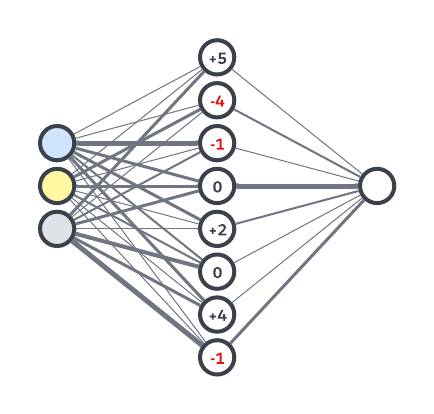
This is our new model. More connections will hopefully mean better estimates. This web of connections, guided by weights and biases, is an example of a neural network. We call it that because the connections, forged by experience (data), resemble how the neurons in a brain are connected.
And while scenario is a good beginner word for describing a unique combination of factors, we should really use the word node for that concept. It’s what AI experts use, so moving forward we’ll use it too.
Adding Complexity to Neural Networks
Our new milk run model is a pretty basic example of a neural network. In practice, they can get quite complex. Let’s explore some of the ways researchers set up neural networks to get better results for specific tasks.
First, you might be wondering why we chose eight nodes to stand between our inputs and output. There’s actually some flexibility in that number. We know that having no nodes at all will give us rough estimates. In the same way, having too few might not capture all of the nuance of the system we’re trying to model. But having too many nodes is a problem, too. We don’t want to make the computer do more calculations than necessary. So there’s a sweet spot for the number of nodes where we get good results for the least effort. Choosing the right number is part of designing a good neural network.
There’s something else we can do to make artificial neural networks more like our own, organic ones. It has to do with how our minds often leap from idea to idea to find connections between two things that are not obviously related. Some of the most brilliant insights are the result of several leaps. So, what if we could make a neural network that could make more leaps, too? We can! We do it by adding more nodes as layers, connecting each node to its neighbor.
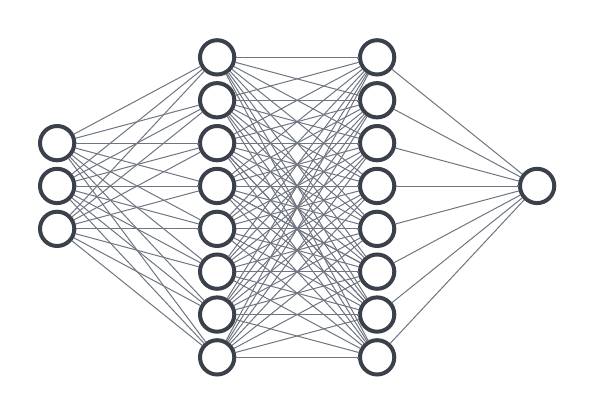
Training AI by adding extra layers to find hidden meaning in data is what’s called deep learning. Thanks to an abundance of computing power, many neural networks are designed to have multiple layers. Again, the best number of layers is a balance between the number of calculations required and the quality of results they produce.
More Than Mental Math, It’s Neural Network Math
So, about those calculations. Up to this point we’ve glossed over the math part of training neural networks. That’s for a few reasons. First, the math can get really complicated, really fast. For example, here’s a snippet of a research paper about neural networks.
Yeah, it’s intense!
Second, the exact math is going to depend on what kind of task you’re training the neural network to do. Third, each new research paper updates the math as we learn what works better at training different models.
So, designing a neural network involves choosing the number of nodes, layers, and the appropriate math for the task it’s training for. With the model architecture ready, you have to let the computer use all that fancy math to do its guess-and-check routine. Eventually it’ll figure out the best weights and biases to give good estimates.
And this brings us to something that’s a little unsettling about artificial neural networks. Imagine a skilled talent scout who’s looking for the next great baseball player. “I’ll know them when I see them,” they might say. They can’t explain how they’ll know, they just will. In the same way, our neural network can’t explain why certain factors are important. Sure, we can look at the values attached to each weight and bias, but the relevance of a number that’s the result of a connection of a connection of a connection will be lost to us.
So just like how the mind of the talent scout is a black box, so is our neural network. Because we don’t observe the layers between the input and output, they’re referred to as hidden layers.
Wrap Up
To summarize, neural networks are a mix of nodes, layers, weights, biases, and a bunch of math. Together they mimic our own organic neural networks. Each neural network is carefully tuned for a specific task. Maybe it’s great at predicting rain, maybe it categorizes plants, or maybe it keeps your car centered in the lane on the highway. Whatever the task, neural networks are a big part of what makes AI seem magical. And now you know a little bit about how the trick is done.
Resources